Tìm số nghiệm của phương trình lượng giác trong khoảng, đoạn - Chuyên đề Toán 11
Ví dụ minh họa
Ví dụ 1. Phương trình 2sin2x+ 4cosx = 0 có bao nhiêu nghiệm trong khoảng (0; 3000)
A. 954
B. 955
C. 956
D. 957
Bài giải:
Ta có: 2sin2x + 4cosx = 0
⇒ 4. sinx. cos+ 4cosx= 0
⇒ 4cosx. ( sinx+ 1) = 0
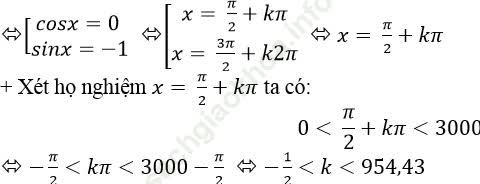
Mà k nguyên nên k∈ {0; 1; 2; 3; …; 954} có 955 giá trị của k thỏa mãn.
⇒ Phương trình có 955 nghiệm thuộc khoảng (0; 3000)
Chọn B.
Ví dụ 2. Cho phương trình 2sinx+ 2cosx – cos2x=0. Tìm số nghiệm của phương trình thuộc (0; 2000).
A. 624
B. 652
C. 645
D. 636
Bài giải:
Ta có: 2sinx+ 2cosx – cos2x = 0
⇒ (2sinx+ 2cosx) – (cos2 x – sin2 x)= 0
⇒ 2 (sinx + cosx) - (cosx- sinx). (cosx+ sinx)= 0
⇒ (sinx+ cosx). (2- cosx + sinx) = 0
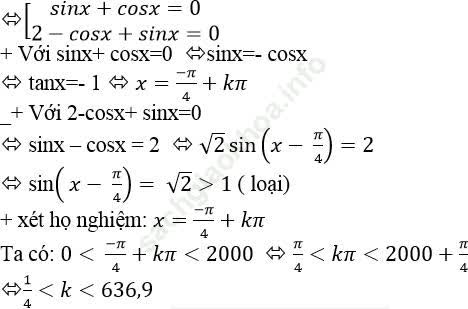
Mà k nguyên nên k∈ {1; 2; 3.. ;635; 636}. Do đó; phương trình đã cho có 636 nghiệm trong khoảng (0; 2000)
Chọn D.
Ví dụ 3. Phương trình 2cos2 x+ 2cos22x + 2cos23x – 3= cos4x. (2sin2x+ 1) có bao nhiêu nghiệm thuộc khoảng (10; 1000)?
A. 1207
B. 1260
C. 1261
D. 1208
Bài giải:
Ta có: 2cos2 x+ 2cos22x + 2cos23x – 3= cos4x
⇒ 1+ cos2x + 1+ cos4x + 1+ cos6x- 3 = 2. cos4x. sin2x + cos4x
⇒ cos2x+ cos4x+ cos6x = 2cos 4x. sin2x + cos4x
⇒ cos2x+ cos6x – 2cos 4x. sin2x=0
⇒ 2cos 4x. cos2x – 2. cos4x. sin2x= 0
⇒ 2cos 4x. (cos2x – sin2x) = 0
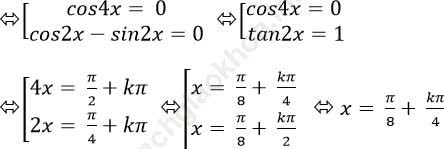
⇒ 12,23 < k < 1272,8
Mà k nguyên nên k∈ {13; 14; …1271; 1272}
⇒ có 1260 số thỏa mãn.
Chọn B.
Ví dụ 4. Phương trình
A. 3025
B. 3026
C. 3027
D. Tất cả sai
Bài giải:
Điều kiện: ( 1+2cosx).sinx ≠ 0
Với điều kiện trên phương trình trên tương đương:
( 1- 2cosx). (1+ cosx) = (1+ 2cosx). sinx
⇒ 1+ cosx – 2cosx – 2cos2 x= sinx + 2sinx. cosx
⇒ 2cos2 x – 1 + cosx+ sinx + 2sinx. cosx= 0
⇒ cos2x + cosx + sinx + sin2x=0
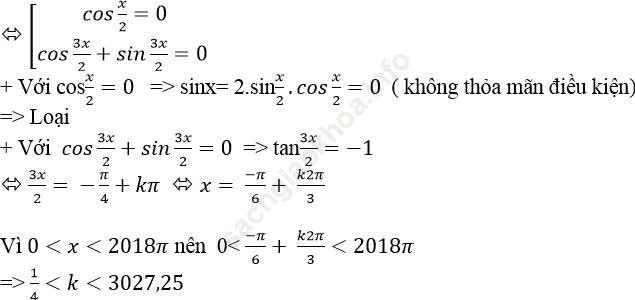
Mà k nguyên nên k∈ {1; 2; 3; .. ; 3027}
⇒ Phương trình đã cho có 3027 nghiệm.
Chọn C.
Ví dụ 5. Phương trình
A. 1
B. 2
C. 3
D. 4
Bài giải:
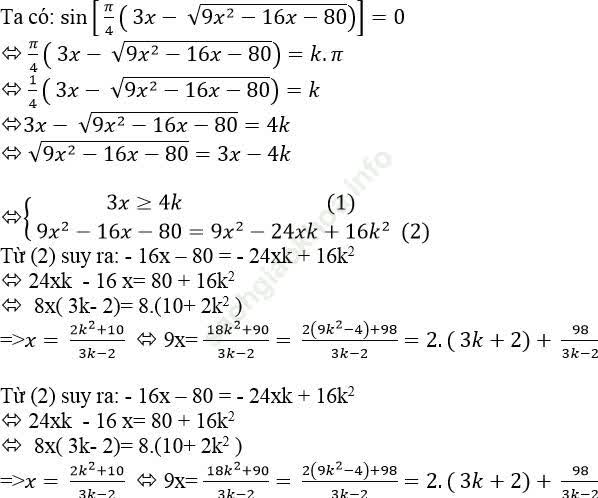
Vì x nguyên dương nên (3k- 2)∈Ư (98)= {1; 2; 7; 14; 49; 98}
Từ đó ta tính được k∈ {1; 3; 17} – chú ý k nguyên.
+ k= 1 ⇒ x= 12
+ k= 3 ⇒ x = 4
+ k= 17 ⇒ x = 12
⇒ Phương trình có hai nghiệm nguyên dương là 12 và 4
Chọn B.
Ví dụ 6. Phương trình:
A. 4033
B. 4032
C. 4035
D. 4036
Bài giải:
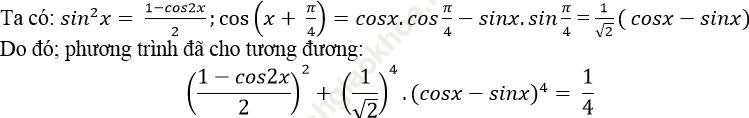
⇒ (1- cos2x)2 + (cosx- sinx)4=1
⇒ 1- 2cos2x + cos22x + (cos2x + sin2x – 2. cosx. sinx)2= 1
⇒ 1- 2cos2x + cos22x + (1- sin2x)2 - 1= 0
⇒ - 2cos2x + cos22x + 1- 2sin2x+ sin22x = 0
⇒ (cos22x + sin22x) +1 – 2. (cos2x+ sin2x)= 0
⇒ 2- 2 (cos2x + sin2x) = 0
⇒ cos2x + sin2x = 1

Mà k nguyên nên k∈ {0; 1; 2;... ; 2016} ⇒ có 2017 nghiệm
Kết hợp 2 trường hợp có 4033 nghiệm trong khoảng đang xét.
Chọn A.
Ví dụ 7. Tìm số nghiệm của phương trình: tan4x – tan2x – 4tanx= 4tan4x. tan2x. tanx trên đoạn [0; 2π]?
A. 6
B. 7
C. 8
D. 9
Bài giải:
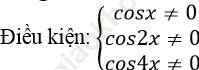
Ta có: tan4x – tan2x – 4tanx = 4tan4x. tan2x. tanx
⇒ tan4x – tan2x = 4tan4x. tan2x. tanx + 4 tanx
⇒ tan4x - tan2x = 4tanx. (tan 4x. tan2x + 1)

Chọn B.
Ví dụ 8. Tính tổng các nghiệm của phương trình
A. π/4
B. π/3
C. π
D. Đáp án khác
Bài giải:
Điều kiện:
Ta có: tan 3x + cot (π/2+x)=0
⇒ tan3x – tanx = 0 ⇒ tan3x= tanx
⇒ 3x = x+kπ ⇒ 2x= kπ
⇒ x= kπ/2 (không thỏa mãn điều kiện)
Do đó; phương trình đã cho vô nghiệm.
Chọn D.
Ví dụ 9. Tìm số nghiệm của phương trình sin (cosx) = 0 trên khoảng (0; 4π)?
A. 2
B. 3
C. 4
D. 5
Bài giải:
Ta có: sin (cosx)=0
⇒ cosx = kπ (*)
Do với mọi x ta luôn có: - 1 ≤ cosx ≤ 1 nên từ (*) suy ra: k= 0
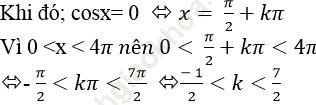
Mà k nguyên nên k∈ {0; 1; 2; 3}.
⇒ Phương trình đã cho có 4 nghiệm trên khoảng (0; 4π)
Chọn C.
Ví dụ 10: Cho phương trình: 2cos23x + (3- 2m)cos3x + m-2= 0. Tìm tất cả các giá trị thực của m để phương trình có đúng ba nghiệm thuộc khoảng
A. 1 < m < 2
B. 2 < m ≤ 3
C. 1 < m ≤ 2
D. 2 < m < 3
Bài giải:

Chọn C.
C. Bài tập vận dụng
Câu 1: Cho phương trình: (cos4 x- sin4 x). (2cos2x+5) – 3 = 0. Tìm số nghiệm của phương trình trên khoảng (π; 4π)
A. 5
B. 7
C. 6
D. 8
Ta có: (cos4 x- sin4 x). (2cos2x+ 5) – 3 = 0.
⇒ (cos2 x- sin2 x). (cos2 x+ sin2x). (2cos 2x + 5) – 3= 0
⇒ cos2x. 1. (2cos 2x + 5) - 3= 0
⇒ 2cos22x + 5cos 2x – 3=0

⇒ Phương trình có ba nghiệm đối với họ nghiệm này.
Kết hợp cả hai trường hợp; suy ra phương trình đã cho có 6 nghiệm thuộc (π; 4π)
Chọn C.
Câu 2:Tìm số nghiệm của phương trình
A. 3
B. 4
C. 5
D. 6

Chọn B.
Câu 3:Tìm số nghiệm của phương trình: sinx. cosx + |sinx+cosx|= 1 trên (0; 2π)?
A. 2
B. 4
C. 3
D. 5

⇒ 0 < k < 4 mà k nguyên nên k∈ {1; 2; 3}.
Vậy phương trình có ba nghiệm trên khoảng đang xét.
Chọn C.
Câu 4:Tìm số nghiệm của phương trình
A. 6
B. 7
C. 8
D. 9
Điều kiện: cosx ≠ -√ 3/2
Với điều kiện trên phương trình đã cho tương đương với phương trình:
2sin2 x-cosx+2-5sinx+sin2x = 0
⇒ (sin2x – cosx) + (2sin2x – 5sinx + 2) =0
⇒ (2sinx. cosx – cosx) + (2sin2x – 5sinx + 2) = 0
⇒ cosx. ( 2sinx- 1) + (sinx- 2). (2sinx – 1)= 0
⇒ (2sinx – 1). (cosx + sinx- 2) = 0
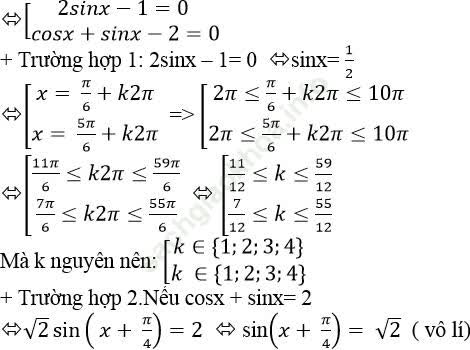
Kết hợp 2 trường hợp; suy ra phương trình có tất cả 8 nghiệm trên đoạn [2π; 10π]
Chọn C.
Câu 5:Tìm số nghiệm của phương trình: cos2x. (tan2 x – cos2x)= cos3x- cos2 x+ 1 trên khoảng (0; 6π)?
A. 9
B. 8
C. 10
D. 11
IMG_2
+ Trường hợp 1: Nếu cosx=- 1
⇒ x= π+k2π. Ta có: 0 < x < 6π nên: 0 < π+k2π < 6π

⇒ Kết hợp hai trường hợp suy ra số nghiệm của phương trình thuộc khoảng (0; 6π) là 9 nghiệm.
Chọn A.
Câu 6:Cho phương trình: m. sin2x – 3sinx. cosx – m- 1 = 0. Gọi S là tập tất cả các giá trị nguyên của m thuộc đoạn [-4; 7] để phương trình có đúng ba nghiệm thuộc (0; 3π/2). Số các phần tử của tập S là:
A. 4
B. 3
C. 5
D. 6
Ta có: m. sin2 x – 3sinx. cosx – m- 1= 0
⇒ m. ( sin2 x- 1) - 3sinx. cosx – 1=0
⇒ - m. cos2 x – 3sinx. cosx – 1=0
⇒ m. cos2 x+ 3sinx. cosx + 1= 0
+ Nhận thấy cosx=0 không thỏa phương trình.
Chia hai vế phương trình cho cos2x ta được:
⇒ tan2 x+3tanx + m+ 1=0 (*)
Đặt t= tanx; phương trình (*) trở thành: t2 + 3t + m + 1= 0
Để phương trình đã cho có ba nghiệm thuộc (0; 3π/2) khi và chỉ khi phương trình (*) có hai nghiệm trái dấu
⇒ a. c= m+ 1 < 0 ⇒ m < - 1
Mà m nguyên và m∈ [-4; 7]
⇒ m∈ {-4; -3; -2}.
⇒ Tập S có 3 phần tử.
Chọn B.
Câu 7:Cho phương trình: ( cosx+ 1). (4cos 2x – m. cosx)= m. sin2 x. Số các giá trị nguyên của m để phương trình có đúng hai nghiệm thuộc đoạn [0; 2π/3] là:
A. 1
B. 2
C. 3
D. 4
Ta có: (cosx+ 1). (4cos2x – m. cosx) = m. sin2x
⇒ (cosx+ 1). (4cos2x – m. cosx) = m. (1- cos2 x)
⇒ (cosx+ 1). (4cos2x- m. cosx) – m. ( 1- cosx). (1+ cosx) =0
⇒ (cosx+ 1)( 4cos2x -m. cosx - m+m. cosx)= 0
⇒ (cosx+ 1). (4cos 2x – m) = 0

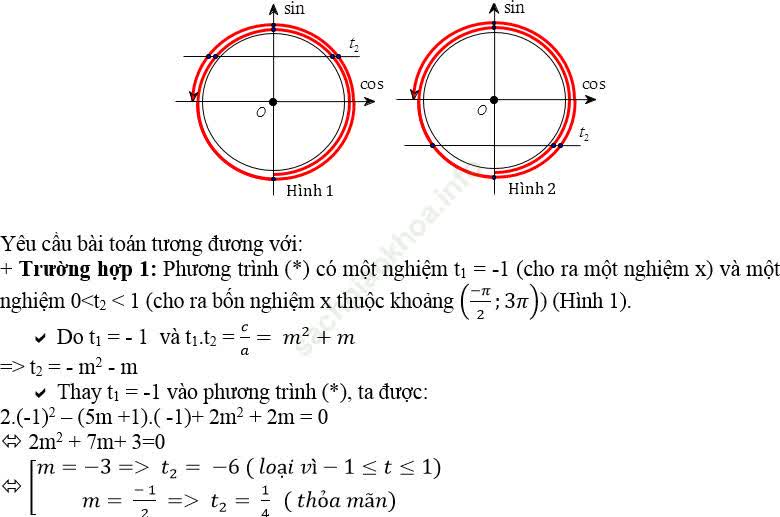
Câu 8:Có bao nhiêu giá trị của m để phương trình: (sinx-1). [2cos2x- (2m+1).cosx + m]=0 có đúng bốn nghiệm thuộc đoạn [0; 2π]
A. 1
B. 2
C. 3
D. 4
Ta có: (sinx- 1). [2cos2 x – (2m+ 1).cosx + m] = 0
⇒ (sinx -1). (2cosx- 1). (cosx – m) = 0

Kết luận: Vậy có hai giá trị của m thỏa mãn.
Chọn B.
Câu 9:Biết rằng khi m= m0 thì phương trình: 2sin2 x – (5m+ 1).sinx +2m2 + 2m = 0 có đúng 5 nghiệm thuộc khoảng
A. m0= - 2
B. m0= 1
C.
D.
Đặt t= sinx (- 1 ≤ t ≤ 1).
Phương trình đã cho trở thành: 2t2 – (5m+1).t + 2m2 + 2m=0 (*)

Chọn D.