Dạng 3: Phương trình bậc nhất theo sinx và cosx - Chuyên đề Toán 11
A. Phương pháp giải & Ví dụ
Xét phương trình asinx + bcosx = c (1) với a, b là các số thực khác 0.
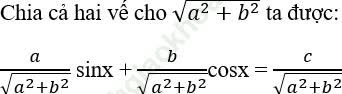
Khi đó phương trình (1) được đưa về dạng: ![]()
Ở đó α là cung thỏa mãn:
Lưu ý:
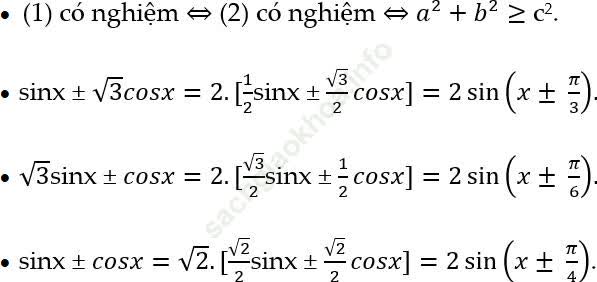
Ví dụ minh họa
Bài 1: Giải phương trình sau: cos2x – sin2x = 0.

Bài 2: Giải phương trình: sin3x - √ 3 cos3x = 2sin2x.
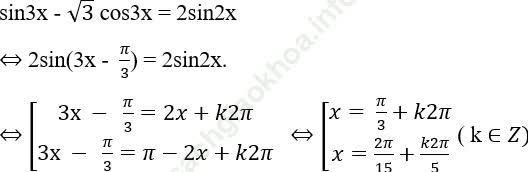
B. Bài tập vận dụng
Bài 1: 3sinx + 4cosx = 0.
Bài giải:
3sinx + 4cosx = 0.
⇔ 3/5 sinx + 4/5 cosx = 0
⇔ cos (x-α) = 0 với α là góc thảo mãn: cosα = 4/5; sinα = 3/5
⇔ x - α = π /2 + kπ
⇔ x = π /2 + α + kπ (k ∈ Z)
Bài 2: sin7x – cos2x = √ 3 (sin2x-cos7x).
Bài giải:
⇔ sin7x + √ 3cos7x = cos2x + √ 3sin2x
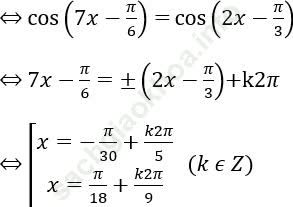
Bài 3: Hàm số sau có tất cả bao nhiêu giá trị nguyên?
Bài giải:
![]()
⇔ (y - 2) sin2x - (y - 1) cos2x = -3y
⇔ (3y)2 ≤ (y - 2)2 + (y + 1)2
⇔ 7y2 + 2y - 5 ≤ 1
⇔ -1 ≤ y ≤ 5/7
Mà y nguyên ⇒ y ∈ {-1; 0}
Bài 4: Giải phương trình: ![]()
Bài giải:
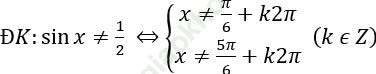
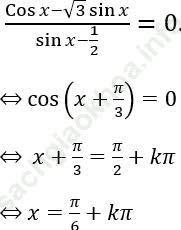
Bài 5: Tìm nghiệm dương nhỏ nhất x0 của phương trình:
3sin3x - √ 3cos9x = 1 + 4sin33x.
Bài giải:
3 sin3x - √ 3 cos9x = 1 + 4sin33x
