Đạo hàm của các hàm số đơn giản - Chuyên đề Toán 11
A. Phương pháp giải
Đạo hàm của các hàm số cơ bản:
Trong đó: u = u (x); v = v (x) là các hàm số có đạo hàm tại điểm x thuộc khoảng xác định.
B. Ví dụ minh họa
Ví dụ 1. Đạo hàm của hàm số y = 2017 là:
A. 2017
B. -2017
C. 0
D. 1
Bài giải:
Hàm số y = 2017 là hàm hằng nên y' = 0
Đáp án đúng là: C
Ví dụ 2. Cho hàm số y = f (x) = 27 - 27x. Trong các mệnh đề sau, mệnh đề nào đúng?
A. f' (x)=27
B. f' (x)= - 27
C. f' (x)=27x
D. f' (x)=1-27x
Bài giải:
Ta có: f' (x) = (27 - 27x)' = (27)' - (27x)' = 0 - 27 = -27
Đáp án đúng là: B.
Ví dụ 3. Cho hàm số y = 2x2 + 2x - 10. Tính đạo hàm của hàm số đã cho
A. 4x+ 2
B. 4x- 10
C. 2x+ 2
D. không tồn tại.
Bài giải:
Ta có: f' (x) = (2x2 + 2x - 10)' = 2 (x2)' + 2. x' - (10)' = 2.2x + 2.1 - 0
⇒ f’ (x) = 4x + 2
Đáp án đúng là: A
Ví dụ 4. Đạo hàm của hàm số y = f (x) = x5 – 3x2 + 6x - 10 là:
A. x5- 6x + 6
B. x4- x2+ 6
C. 5x4 – 3x + 6
D. 5x4- 6x+ 6
Bài giải:
Ta có: f' (x) = (x5-3x2+6x-10)'= (x5)'-3 (x2)'+6. (x)'- (10)'
⇒ f’ (x) = 5x4 – 6x + 6
Đáp án đúng là: D.
Ví dụ 5. Đạo hàm của hàm số y = f (x) = (x+1)( 3- 2x) bằng biểu thức nào sau đây?
A. 3x- 2
B. 1- 4x
C. 2- 4x
D. 1+ 2x
Bài giải:
Áp dụng công thức: (u. v)' = u'. v+u. v' ta có:
f' (x) = (x+1)'. ( 3-2x)+ (x+1). (3-2x)'
⇒ f' (x) = 1. ( 3-2x)+ (x+1). (-2) = 3- 2x- 2x- 2= 1- 4x
Đáp án đúng là: B.
Ví dụ 6. Đạo hàm của hàm số y = f (x) = (x- 1)2( x- 3) bằng biểu thức nào?
A. 2x3- 2x+ 1
B. 3x2- 10x + 7
C. 2x2+ 5x – 7
D. 4x2 – 2x + 8
Bài giải:
+ Áp dụng công thức: (u. v)' = u'. v+u. v' ta có:
⇒ f' (x) = [(x-1)2]'. ( x-3)+ (x-1)2 (x-3)'
= 2 (x-1) (x-3) + (x-1)2. 1 = 2 (x2 – 3x- x + 3) + x2 – 2x+ 1
= 2x2- 6x – 2x+ 6+ x2 – 2x + 1 = 3x2 – 10x + 7
Đáp án đúng là: B.
Ví dụ 7. Tính đạo hàm của hàm số y = (2x+1)/ (x-3)?
 Bài giải:
Bài giải:
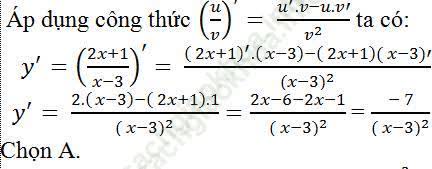
Ví dụ 8. Tính đạo hàm của hàm số y = (x2 - 2x - 1)/ (x - 1)?

Hướng dẫn giải
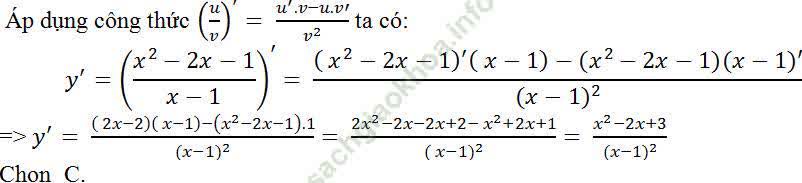
Ví dụ 9. Tính đạo hàm của hàm số: y = 2√x + 2x2 - 1?
A. 1/√x + 4x
B. 2 1/√x + 4x - 2
C. 1/ (2√x) + 4x
D. Tất cả sai
Bài giải:
Ta có: y' = (2√x+2x2-1)' = 2. (√x)'+2. (x2)'- (1)'
=2.1/ (2√x)+2.2x-0 = 1/√x+4x
Đáp án đúng là: A.
Ví dụ 10. Tính đạo hàm của hàm số: y = (√x + 1). (x - 1)

Bài giải
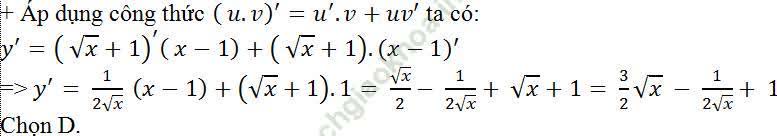
Ví dụ 11. Tính đạo hàm của hàm số: y= 2√x + 2x2 – 2x+ 10

Bài giải:
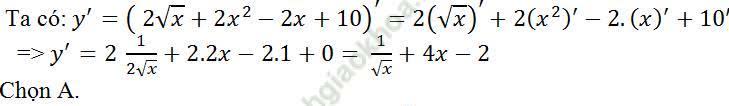
Ví dụ 12. Tính đạo hàm của hàm số y = 2/x + x4 + 4x - 29

Bài giải:
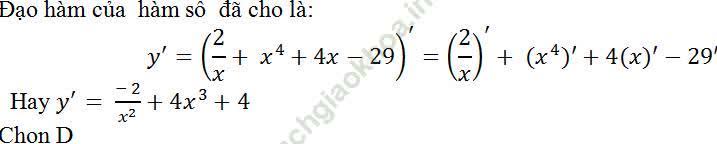
C. Bài tập vận dụng
Câu 1: Đạo hàm của hàm số y = - 18√2 là:
A. - 18 B. 18 C. - 18√2 D. 0
Hàm số y= - 18√2 là hàm hằng nên y'=0
Chọn D.
Câu 2: Cho hàm số y = f (x) = - 2x + 10. Trong các mệnh đề sau, mệnh đề nào đúng?
A. f' (x)=2 B. f' (x)= - 2 C. f' (x)=10 D. f' (x)=-10
Ta có: f' (x)= (-2x+10)'= (-2x)'+ (10)'=-2-0= -2
Chọn B.
Câu 3: Cho hàm số y= -x2 - 7x + 8. Tính đạo hàm của hàm số đã cho
A. –x- 7 B. 2x + 7
C. 2x - 7 D. -2x- 7
Ta có: f' (x)= (-x2-7x+8)'=- (x)'-7. (x)'+ (8)'=-2x-7.1+0
⇒ f’ (x)= -2x - 7
Chọn D.
Câu 4: Đạo hàm của hàm số y= f (x)= 2x4 + 2x2 + x + 28 là
A. 8x3 +2x + 1 B. 8x3 +4x+ 1
C. 8x4 + 4x + 1 D. 4x3 +2x+ 1
Ta có: f' (x)= (2x4+2x2+x+28)'=2 (x4)'+2 (x2)'+ (x)'+ (28)'
⇒ f’ (x)= 8x3 +4x + 1
Chọn B.
Câu 5: Đạo hàm của hàm số y= f (x)= (x- 6)(8- 4x) bằng biểu thức nào sau đây?
A. 32- 8x B. 6x- 24 C. - 4x + 32 D. 2x+ 16
Áp dụng công thức: (u. v)'=u'. v+u. v' ta có:
f' (x)= (x-6)'. ( 8-4x)+ (x-6). (8-4x)'
⇒ f' (x)= 1. ( 8 - 4x)+ (x- 6). (-4) = 8- 4x – 4x + 24 = -8x + 32
Chọn A.
Câu 6: Đạo hàm của hàm số y=f (x)= (x+ 2)( x- 3) bằng biểu thức nào?
A. x+ 1 B. 2x- 1 C. 3x+ 2 D. x2- 1
+ Áp dụng công thức: (u. v)'=u'. v+u. v' ta có:
⇒ f' (x)= (x+2)'. (x-3)+ (x+2). (x-3)'
= 1. (x-3) + (x+2). 1 = x- 3+ x+ 2
= 2x - 1
Chọn B.
Câu 7: Tính đạo hàm của hàm số y= (x-6)/ (2x+3)?
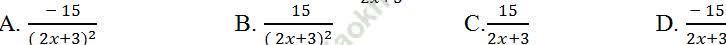
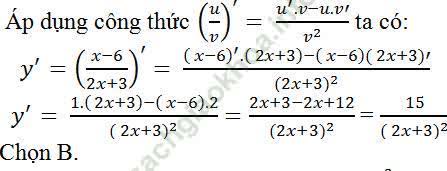
Câu 8: Tính đạo hàm của hàm số y= (x2+x+1)/ (1-x)?

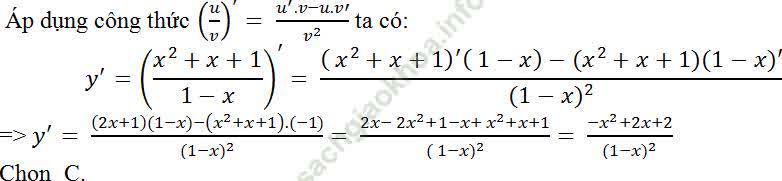
Câu 9: Tính đạo hàm của hàm số: y= (x+2)/ (x2-1)?

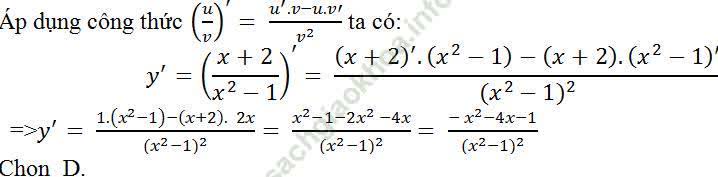
Câu 10: Tính đạo hàm của hàm số: y=4√x - 4x4 + 2x?

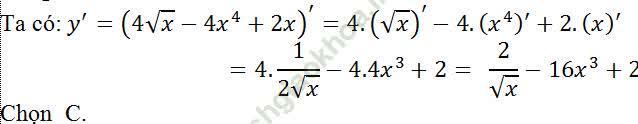
Câu 11: Tính đạo hàm của hàm số: y= (2√x-2). (2x+1)

+ Áp dụng công thức (u. v)'=u'. v+uv' ta có:
y'= (2√x-2)' (2x+1)+ (2√x-2). (2x+1)'
⇒ y'= 2.1/ (2√x) (2x+1)+ (2√x-2).2
= 2√x+ 1/√x+ 4√x-4= 6√x+ 1/√x-4
Chọn A.
Câu 12: Tính đạo hàm của hàm số y= x3/3+2x2- 1/x?
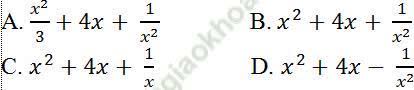
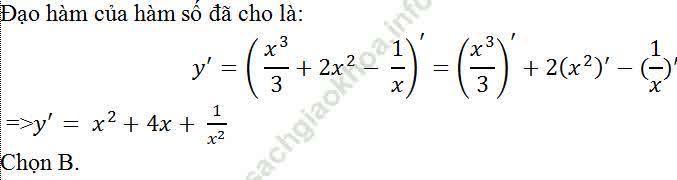
Câu 13: Tính đạo hàm của hàm số: y= (x2+2x)/ (x2-3x+1)

Áp dụng công thức đạo hàm của một thương ta có: