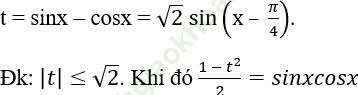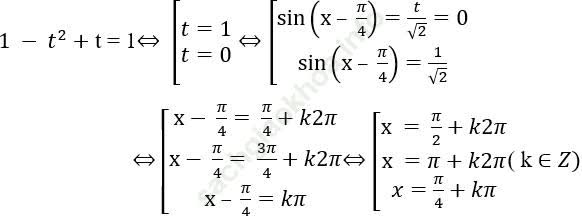Dạng 5: Phương trình lượng giác đối xứng, phản đối xứng - Chuyên đề Toán 11
A. Phương pháp giải & Ví dụ
Định nghĩa: Phương trình đối xứng là phương trình có dạng:
a (sinx + cosx) + bsinxcosx + c = 0 (3)
Hướng dẫn giải:
Để giải phương trình trên ta sử dụng phép đặt ẩn phụ:
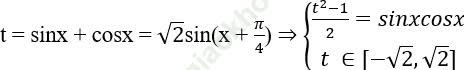
Thay vào (3) ta được phương trình bậc hai theo t.
Ngoài ra, chúng ta còn gặp phương trình phản đối xứng có dạng:
a (sinx - cosx) + bsinxcosx + c = 0 (4)
Để giải phương trình này ta cũng đặt:
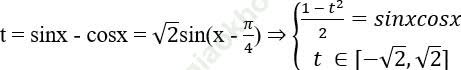
Thay vào (4) ta có được phương trình bậc hai theo t.
Ví dụ minh họa
Bài 1: Giải phương trình sau: 2 (sinx + cosx) + 3sin2x = 2.
=> Phương trình đã cho có dạng:

Bài 2: Cho x thỏa mãn phương trình sin2x + sinx – cosx = 1. Tính sin (x - π/4).

B. Bài tập vận dụng
Bài 1: Giải phương trình sinxcosx + 2 (sinx + cosx) = 2.
Bài giải:
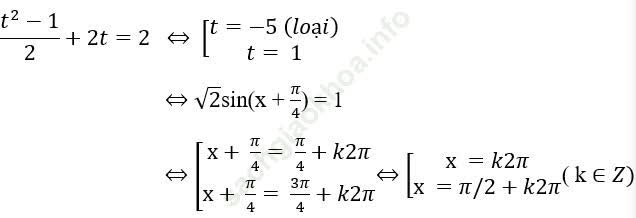
Bài 2: Tìm nghiệm dương nhỏ nhất của phương trình: 3 (sinx + cosx) + 2sin2x = -3
Bài giải:


Bài 3: Cho x thỏa mãn phương trình: sinx + cosx - 4sinxcosx – 1 = 0. Tính sin (x + π /4).
Bài giải:

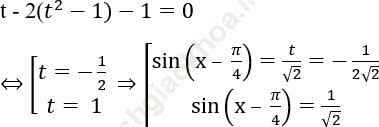
Bài 4: Giải phương trình sau: sin2x – 4 (cosx – sinx) = 4.
Bài giải:
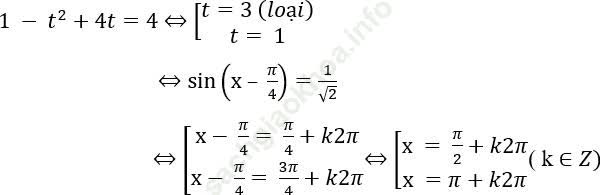
Bài 5: Giải phương trình: sin2x + √ 2sin (x - π /4) = 1
Bài giải: