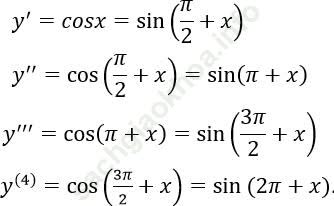Dạng 2: Tìm đạo hàm cấp cao của hàm số - Chuyên đề Toán 11
A. Phương pháp giải & Ví dụ
Đạo hàm cấp hai: Cho hàm số f (x) có đạo hàm f ’ (x). Nếu f ’ (x) cũng có đạo hàm thì đạo hàm của nó được gọi là đạo hàm cấp hai của f (x) và được kí hiệu là: f '' (x), tức là:
f ’’ (x) = (f’ (x))’
Đạo hàm cấp n: Cho hàm số f (x) có đạo hàm cấp n – 1 (với n ∈ N, n ≥ 2)) là f(n-1)(x). Nếu f(n-1)(x) cũng có đạo hàm thì đạo hàm của nó được gọi là đạo hàm cấp n của f (x) và được kí hiệu là f(n)(x), tức là: f(n)(x) = (f(n-1)(x))'
Để tính đạo hàm cấp n:
+ Tính đạo hàm cấp 1,2,3, ... , từ đó dự đoán công thức đạo hàm cấp n
+ Dùng phương pháp quy nạp toán học để chứng minh công thức đúng.
Ví dụ minh họa
Bài 1: Hàm số: 
.Tính đạo hàm cấp 2 của hàm số trên.
Bài giải:
Ta có:
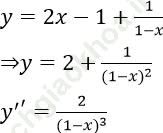
Bài 2: Hàm số y = (x) = cos (2x - π /3). Phương trình f(4)(x) = -8 có nghiệm x ∈ [0; π /2] là:
Bài giải:
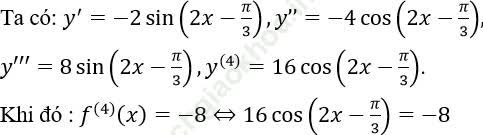
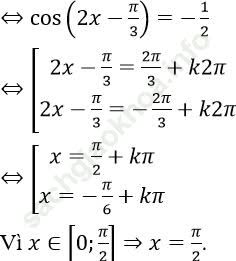
Bài 3: Cho hàm số f (x) = 5 (x+1)3 + 4 (x+1). Tìm tập nghiệm của phương trình f '' (x) = 0?
Bài giải:
Ta có: f ' (x) = 15 (x+1)2 + 4;
f '' (x) = 30 (x+1) ⇒ f '' (x) = 0
⇔ x = -1
Bài 4: Cho hàm số y = sin22x. Tính y(4)(π /6)?
Bài giải:
Vì: y ' = 2sin2x (2cos2x) = 2sin4x; y '' = 8cos4x; y ''' = -32sin4x;
y(4) = -128cos4x ⇒ y(4)(π /6) = 64√ 3
Bài 5: Cho hàm số y = sin2x. Tính y’’
Bài giải:
Ta có y' = 2cos2x ⇒ y '' = -4sin2x
Bài 6: Cho hàm số y = sin2x. Tính y '' (π /3), y(4)(π /4)?
Bài giải:
Ta có: y ''' = -8cos2x, y(4) = 16sin2x
=> y ''' (π /3)= --8cos (2π /3) = 4; y(4)(π /4) = 16sin (π /2) = 16
Bài 7: Cho hàm số y = sin2x. Tính y(n)?
Bài giải:
Ta có:
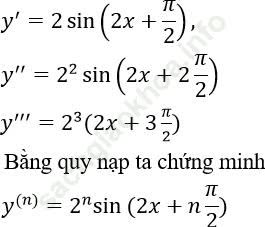
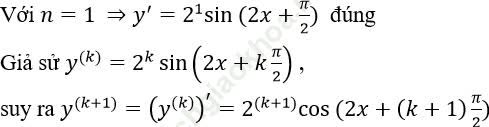
Theo nguyên lí quy nạp ta có điều phải chứng minh.
B. Bài tập vận dụng
Bài 1: Đạo hàm cấp hai của hàm số y = (3/4)x4 - 2x3 - 5x + sinx bằng biểu thức nào sau đây?
A. 9x2-12x+sinx
B. 9x2-12x-sinx
C. 9x2-6x-sinx
D. 9x2-12x+cosx
Đáp án: B
y’ = 3x3 - 6x2 - 5 + cosx. Do đó y” = 9x2 - 12x - sinx. Chọn đáp án B
Bài 2: Đạo hàm cấp 4 của hàm số y = sin2x bằng biểu thức nào sau đây?
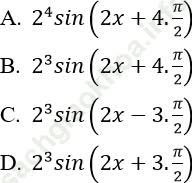
Đáp án: D
y’ = 2sinxcosx = sin2x
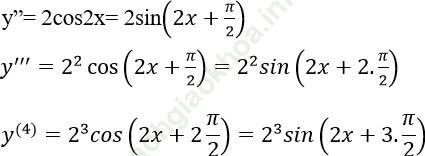
Chọn đáp án D
Bài 3: Đạo hàm cấp hai của hàm số y = 1/ (2x-3) bằng biểu thức nào dưới đây?
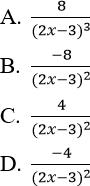
Đáp án: A
Ta có:
Đáp án A
Bài 4: Đạo hàm cấp hai của hàm số y = cosx. cos2x. cos3x bằng biểu thức nào dưới đây?
A. cos2x + 4cos4x + 9cos6x
B. – cos2x - 4cos4x – 9cos6x
C. – cosx - 4cos2x - 9cos3x
D. (-1/4)cos2x + (1/4)cos4x + (-1/4)cos6x
Đáp án: B
Ta có: y = (1/2)(cos3x+cosx)cos3x = (1/4)(cos6x+1+cos4x+cos2x)
Khi đó y ’’ = - cos2x - 4cos4x – 9cos6x
Đáp án B
Bài 5: Đạo hàm cấp 2016 của hàm số y = sinx bằng biểu thức nào sau đây?
A. cosx
B. sinx
C. –sinx
D. –cosx
Đáp án: B
Đáp án B
Ta có:
Vậy đạo hàm cấp 2016 của hàm số đã cho là: sinx
Bài 6: Cho hàm số f (x) = x2015 + 2x2014 + 3x2013 +⋯ + 2015x + 2016. Giá trị f(2016)(x) bằng:
A. 2016!
B. 2015!
C. 2014!
D. 0
Đáp án: D
Đáp án D
Do số mũ cao nhất trong đa thức x2015 + 2x2014 + 3x2013 +⋯ + 2015x + 2016 là 2015 nên f(2016)(x) = 0
Bài 7: Hàm số: 
có đạo hàm cấp hai là:
Đáp án: D
Chọn D.
Ta có
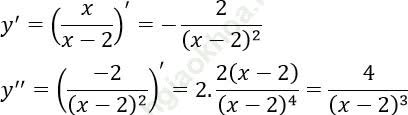
Bài 8: Hàm số y = (x2 + 1)3 có đạo hàm cấp ba là:
A. y ''' = 12 (x2+1)
B. y ''' = 24 (x2+1)
C. y ''' = 24 (5x2+3)
D. y ''' = -12 (x2+1)
Đáp án: C
Chọn C.
Ta có y = x6+3x4+3x2+1; y' = 6x5+12x3+6x
y '' = 30x4+36x2+6; y ''' = 120x3+72x = 24x (5x2+3)
Bài 9: Hàm số: 
có đạo hàm cấp hai bằng:
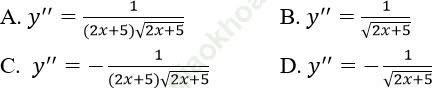
Đáp án: C
Chọn C
Ta có
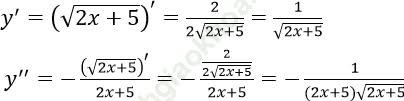
Bài 10: Hàm số: 
có đạo hàm cấp 5 bằng:
Đáp án: A
Chọn A.
Ta có
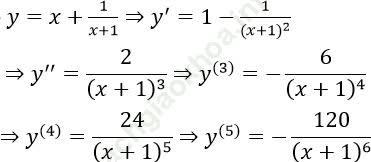
Bài 11: Hàm số: 
có đạo hàm cấp 5 bằng:
Đáp án: A
Chọn A.
Ta có:
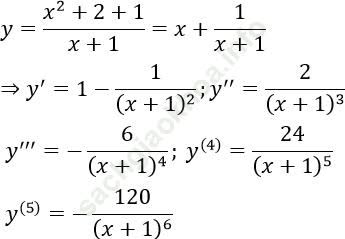
Bài 12: Hàm số: 
có đạo hàm cấp 2 bằng:
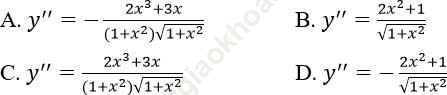
Đáp án: C
Chọn C.
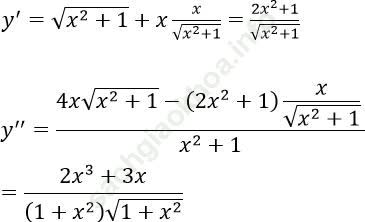
Bài 13: Hàm số y = (2x+5)5 có đạo hàm cấp 3 bằng:
A. y ''' = 80 (2x+5)5
B. y ''' = 480 (2x+5)2
C. y ''' = -480 (2x+5)2
D. y ''' = -80 (2x+5)3
Đáp án: B
Chọn B.
Ta có: y' = 5 (2x+5)4.2 = 10 (2x+5)4; y'' = 80 (2x+5)3; y ''' = 480 (2x+5)2.
Bài 14: Hàm số y = tanx có đạo hàm cấp 2 bằng:
Đáp án: D
Chọn D
Ta có:
Bài 15: Bài 15: Cho hàm số y = sinx. Chọn câu sai.
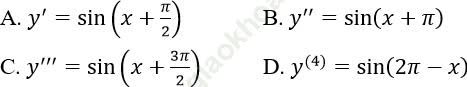
Đáp án: D
Chọn D
Ta có:
