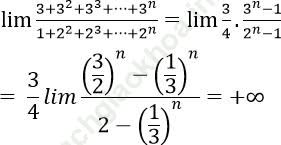Dạng 3: Tính giới hạn của dãy số - Chuyên đề Toán 11
A. Phương pháp giải & Ví dụ
- Ta quan sát, phân tích những đặc điểm của dãy số đề bài cho, từ đó rút ra công thu gọn cho tổng đó (có thể dùng công thức tính tổng của cấp số cộng hoặc cấp số nhân) hoặc biến đổi đại số để giảm bớt những hạng tử trong tổng, …
- Dùng các quy tắc tính giới hạn của dãy số để tính giới hạn của tổng đã cho sau khi đã thu gọn.
Ví dụ minh họa
Bài 1: Cho dãy số (un) với 
. Tính lim un
Bài giải:
un là tổng n số hạng đầu tiên của một cấp số nhân có u1 = 1/2 và q = (-1)/2.
Do đó
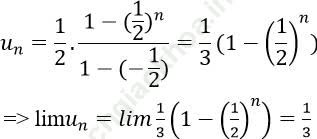
Bài 2: Tính lim 
Bài giải:
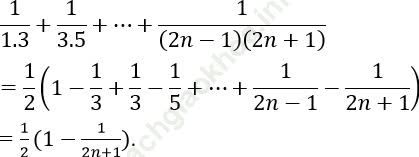
Vậy: 
Bài 3: Tính 
Bài giải:
Ta có: 
Mà:
=> 
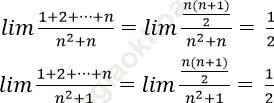
Bài 4: Tính 
Bài giải:
Bài 5: Tính 
Bài giải:
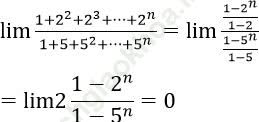
Bài 6: Cho dãy số (un). Biết 
với mọi n ≥ 1. Tìm 
Bài giải:
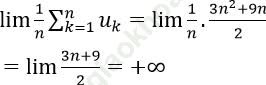
Bài 7: Tính 
Bài giải:
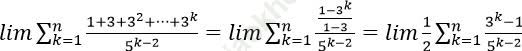
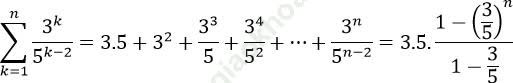
Khi đó
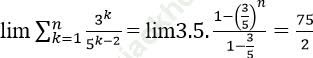
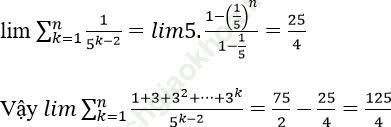
B. Bài tập vận dụng
Bài tập tính giới hạn của dãy số
Bài 1: Tìm giá trị đúng của: 
A. √ 2 + 1. B. 2. C. 2√ 2. D. 1/2.
Đáp án: C
Ta có:
là tổng của cấp số nhân lùi vô hạn với số hạng đầu là 1 và công bội là 1/2. Khi đó:
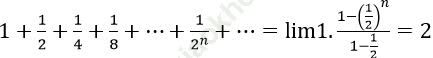
Vậy S = 2√ 2.
Chọn đáp án C.
Bài 2: Tính giới hạn: 
A. 0 B. 1/3 C. 2/3 D. 1
Đáp án: B
Ta có:
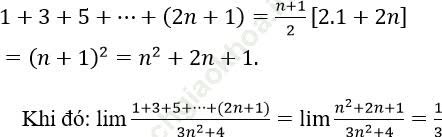
Đáp án B.
Bài 3: Tính giới hạn: 
A. 0 B. 1 C. 3/2 D. Không có giới hạn
Đáp án: B
Ta có:
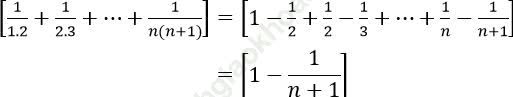
Khi đó
Đáp án B
Bài 4: Tính giới hạn: 
A. 1 B. 0 C. 2/3 D. 2
Đáp án: D
Ta có:
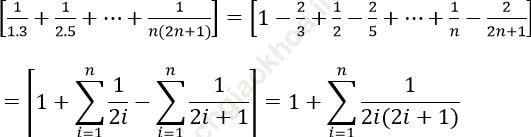
Khi đó
Chọn đáp án D.
Bài 5: Tính giới hạn: 
A. 1/2 B. 1 C. 0 D. 2/3
Đáp án: A
Ta có:
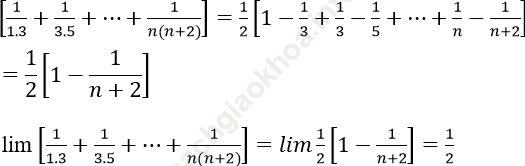
Đáp án A
Bài 6: Tính giới hạn: 
A. 11/18 B. 2 C. 1 D. 3/2
Đáp án: A
Bài 7: Tính giới hạn: 
A. 1 B. 1/2 C. 1/4 D. 3/2
Đáp án: A
Ta có:
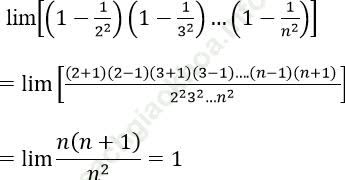
Đáp án A
Bài 8: Cho dãy số (un) với 
. Mệnh đề nào sau đây là mệnh đề đúng?
A. limun = 0
B. limun = 1/2
C. limun = 1
D. Dãy số (un) không có giới hạn khi n → +∞
Đáp án: B
Ta có:
Do đó
Đáp án B
Bài 9: 
bằng.... ?
Đáp án: A
Chọn A.
Từ thức là tổng của n số hạng đầu tiên của cấp số cộng (un) với n = 1, un = 4n-3 và công bội d = 4
Do đó
Tương tự ta có
Vậy
Bài 10: 
bằng:
A. +∞ B. 3 C. 3/2 D. 2/3
Đáp án: A
Chọn A
Ta có từ thức là tổng n số hạng đầu tiên của cấp số nhân (un) với ui = 3 và q = 3
Do đó 3 + 32 + 33 + ⋯ + 3n =
Mẫu thức là tổng của n+1 số hạng đầu tiên của cấp số nhân (vn) với vn = 1 và q = 2.
Do đó
Vậy
