Đoạn vuông góc chung của hai đường thẳng chéo nhau - Chuyên đề Toán 11
A. Phương pháp giải
* Dựng đoạn vuông góc chung và tính độ dài đoạn đó.
Trường hợp 1: Δ và Δ ' vừa chéo nhau vừa vuông góc với nhau
+ Bước 1: Chọn mặt phẳng (α) chứa Δ ' và vuông góc với Δ tại I.
+ Bước 2: Trong mặt phẳng (α) kẻ IJ ⊥ Δ '
Khi đó: IJ là đoạn vuông góc chung và d (Δ, Δ ') = IJ.
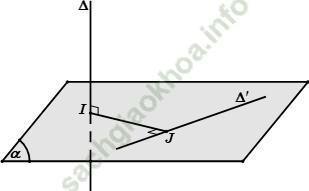
Trường hợp 2: Δ và Δ ' chéo nhau mà không vuông góc với nhau
+Bước 1: Chọn mặt phẳng (α) chứa Δ ' và song song với Δ.
+ Bước 2: Dựng d là hình chiếu vuông góc của Δ xuống (α) bằng cách lấy điểm M ∈ Δ dựng đoạn MN ⊥ (α), lúc đó d là đường thẳng đi qua N và song song với Δ.
+ Bước 3: Gọi H = d ∩ Δ ', dựng HK // MN
Khi đó HK là đoạn vuông góc chung và d (Δ, Δ ') = HK = MN
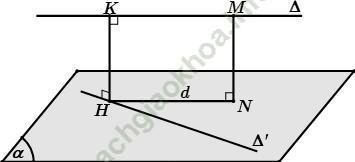
Hoặc:
Bước 1: Chọn mặt phẳng (α) ⊥ Δ tại I.
Bước 2: Tìm hình chiếu d của Δ ' xuống mặt phẳng (α).
Bước 3: Trong mặt phẳng (α), dựng IJ ⊥ d, từ J dựng đường thẳng song song với Δ cắt Δ ' tại H, từ H dựng HM // IJ.
Khi đó HM là đoạn vuông góc chung và d (Δ, Δ ') = HM = IJ.
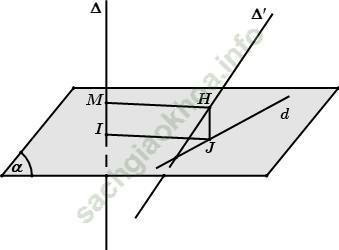B. Ví dụ minh họa
Ví dụ 1: Cho hình chóp S. ABCD có đáy ABCD là hình vuông tâm O; SA vuông góc với đáy (ABCD). Gọi K; H theo thứ tự là hình chiếu vuông góc của A và O lên SD Chọn khẳng định đúng trong các khẳng định sau?
A. Đoạn vuông góc chung của AC và SD là AK
B. Đoạn vuông góc chung của AC và SD là CD
C. Đoạn vuông góc chung của AC và SD là OH
D. Các khẳng định trên đều sai
Hướng dẫn giải
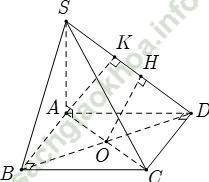
+ Ta xét các phương án:
- Phương án A:
Giả sử AK ⊥ AC, do AK ⊥ AB ⇒ AK ⊥ (ABC)
⇒ AK ≡ SA (vì SA ⊥ (ABC)) ⇒ SA ⊥ SD ⇒ Δ SAD có 2 góc vuông (vô lý)
- Phương án B:
Theo tính chất của hình vuông thì AC và CD không vuông góc với nhau nên đoạn vuông góc chung của AC và SD không phải CD.
- Phương án C:
Giả sử AC ⊥ OH, do AC ⊥ BD ⇒ AC ⊥ (SBD) ⇒ AC ⊥ SO
Lại có: SA ⊥ AC ⇒ vô lý.
⇒ Đoạn vuông góc chung của AC và SD không phải là OH.
Chọn đáp án D
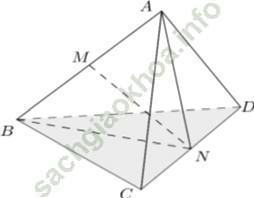
Ví dụ 2: Cho tứ diện đều ABCD có cạnh bằng a. Tính khoảng cách giữa AB và CD.
Hướng dẫn giải
Chọn C
Gọi M và N lần lượt là trung điểm của AB và CD
+ Xét tam giác ACD đều có NA là đường trung tuyến đồng thời là đường cao nên NA = (a√ 3)/2.
Tương tự: NB = (a√ 3)/2.
⇒ NA = NB nên tam giác ANB cân tại N
suy ra đường trung tuyến NM đồng thời là đường cao: NM ⊥ AB
+ Chứng minh tương tự ta có NM ⊥ DC, nên d (AB; CD) = MN.
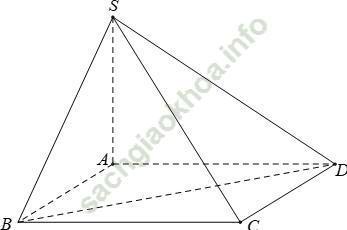
Ví dụ 3: Cho hình chóp S. ABCD có mặt đáy là hình thoi tâm O, cạnh a và ∠ BAD = 60° và SO = 3a/4. Biết SA = SC và SB = SD. Hỏi khoảng cách giữa SA và BD bằng bao nhiêu?
Hướng dẫn giải
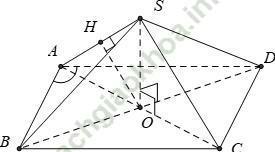
+ Vì SA = SC nên tam giác SAC cân tại S ⇒ SO ⊥ AC
Vì SB = SD nên tam giác SBD cân tại S ⇒ SO ⊥ BD.
+ Ta có:
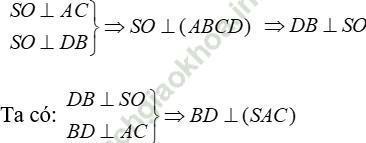
Trong mp (SAC), kẻ OH ⊥ SA (H ∈ SA). Ta chứng minh OH là đoạn vuông góc chung của SA và BD
Ta có: OH ⊥ SA (cách dựng) và OH ⊥BD (vì BD⊥ (SAC)
⇒ OH là đoạn vuông góc chung của SA và BD. Do đó: d (SA; DB) = OH.
Ta có: Tam giác ABD cân tại A có góc A bằng 60° nên tam giác ABD đều cạnh a.
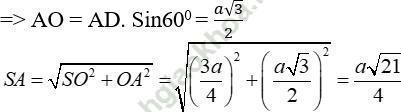
+ Tam giác SOA vuông tại O, có OH là đường cao, ta có:
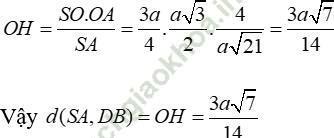
Chọn B
Ví dụ 4: Cho hình chóp S. ABCD có đáy ABCD là hình chữ nhật với AC = a√ 5; BC = a√ 2. Đường thẳng SA vuông góc với mặt phẳng đáy. Tính khoảng cách giữa SD và BC
Hướng dẫn giải
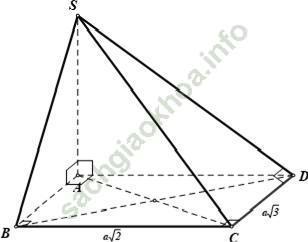
Ta tìm đoạn vuông góc chung của SD và BC:
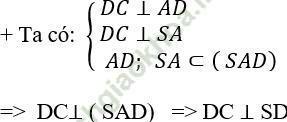
Lại có; DC ⊥ BC nên DC là đoạn vuông góc chung của SD và BC
⇒ d (SD; BC) = DC.
Áp dụng định lí Pyta go vào tam giác vuông ABC có
Chọn đáp án D
Ví dụ 5: Cho tứ diện đều ABCD cạnh a. Khoảng cách giữa hai đường thẳng AB và CD bằng bao nhiêu?
Hướng dẫn giải
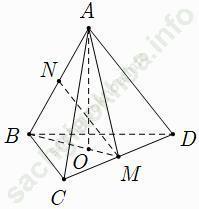
Gọi M; N lần lượt là trung điểm các cạnh CD và AB.
Ta chứng minh MN là đoạn vuông góc chung của AB và CD.
+ Do ABCD là tứ diện đều nên Δ ACD = Δ BCD
⇒ AM = BM
⇒ Tam giác MAB cân tại M có MN là đường trung tuyến nên đồng thời là đường cao.
⇒ MN ⊥ AB
+ Chứng minh tương tự ta có: MN ⊥ CD
⇒ MN là đoạn vuông góc chung của AB và CD.
⇒ d (AB; CD) = MN
+ Ta có: NB = AB/2 = a/2.
Tam giác BCD đều cạnh a nên BM = BC. sin60° = (a√ 3)/2
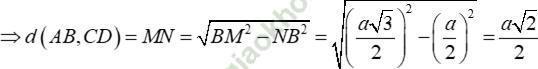
Chọn đáp án B
Ví dụ 6: Cho hình hộp chữ nhật ABCD. A’B’C’D’ có AB = AA’ = a và AC = 2a. Tính khoảng cách giữa AC’ và CD’
Hướng dẫn giải
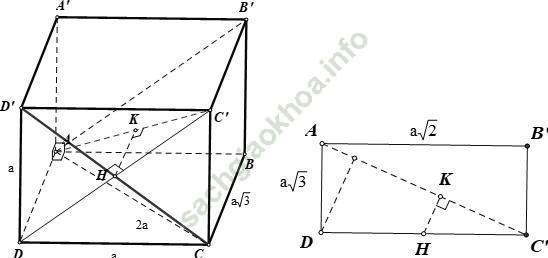
Ta có hình chiếu của AC’ trên mặt phẳng (DCC’D’) là DC' ⊥ D’C nên AC’ ⊥ D'C
⇒ D’C ⊥ (ADC’B’) tại điểm H là trung điểm CD’.
Từ H ta kẻ HK ⊥ AC’
⇒ d (AC’; D’C) = HK (khi đó HK là đoạn vuông góc chung của AC’ và D’C)
Ta tính khoảng cách d từ điểm D đến đường thẳng AC’
+ Áp dụng định li Pytago với tam giác vuông ABC ta có
+ Áp dụng định lí pytago với tam giác vuông DCC’ ta có:
+ Xét tam giác ADC’ có:
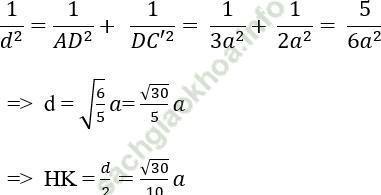
Chọn đáp án D
Ví dụ 7: Cho hình chóp S. ABCD có đáy ABCD là hình vuông tâm O, cạnh a. Biết hai mặt bên (SAB) và (SAD) cùng vuông góc với mặt phẳng đáy và SA = a√ 2. Khoảng cách giữa BD và SC là
A. độ dài của đoạn thẳng OA.
B. Độ dài của đoạn thẳng BC.
C. khoảng cách từ điểm O đến cạnh SC.
D. Khoảng cách từ điểm S đến đoạn BD.
Hướng dẫn giải
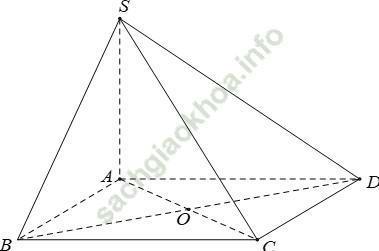
+ Vì hai mặt bên (SAB) và (SAD) cùng vuông góc với mặt phẳng đáy, mà (SAB) ∩ (SAD) = SA
⇒ SA ⊥ (ABCD)
+ Ta có: BD ⊥ SA (vì SA ⊥ (ABCD). Và BD ⊥ AC (vì ABCD là hình vuông)
⇒ BD ⊥ (SAC) tại O, mà SC ⊂ (SAC) nên d (BD; SC) = d (O; SC)
(Chú ý: trong mp (SAC) kẻ OH vuông góc SC thì OH chính là đoạn vuông góc chung của BD và SC).
Chọn đáp án C
C. Bài tập vận dụng
Câu 1: Cho hình chóp S. ABCD có SA ⊥ (ABCD) đáy ABCD là hình chữ nhật với AC = a√ 5 và BC = a√ 2. Tính khoảng cách giữa SD và BC?
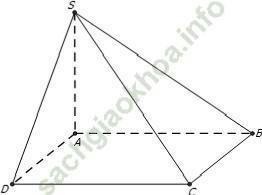
Ta tìm đoạn vuông góc chung của SD và BC:
+ Ta chứng minh CD ⊥ (SAD):
Do CD ⊥ AD (vì ABCD là hình chữ nhật), và CD ⊥ SA (vì SA ⊥ (ABCD))
⇒ CD ⊥ (SAD)
Mà SD ⊂ (SAD) nên CD ⊥ SD (1)
+ Lại có: CD ⊥ BC (vì ABCD là hình chữ nhật) (2)
Từ (1) và (2) suy ra: CD là đoạn vuông góc chung của SD và BC.
⇒ d (SD; BC) = CD
Áp dụng định lí Pytago trong tam giác vuông ABC có:
AB2 = AC2 - BC2 = 5a2 - 2a2 = 3a2
⇒ AB = CD = √ 3a
⇒ d (SD; BC) = CD = √ 3a
Đáp án D
Câu 2: Cho hình chóp tứ giác đều S. ABCD có cạnh đáy bằng a và chiều cao bằng h. Tính khoảng cách giữa hai đường thẳng chéo nhau SA và BD
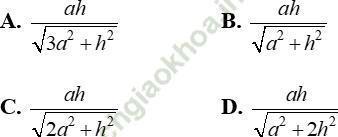
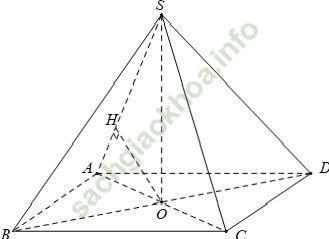
Gọi O là giao điểm của AC và BD; H là hình chiếu của O lên SA.
+ Vì S. ABCD là hình chóp tứ giác đều nên BD ⊥ (SAC) mà OH ⊂ (SAC)
⇒ BD ⊥ OH
Suy ra OH là đoạn vuông góc chung của BD và SA.
+ Ta có: AC = AD. √ 2 = a√ 2 nên AO = (1/2)AC = (a√ 2)/2
Xét tam giác vuông SOA có đường cao OH có:
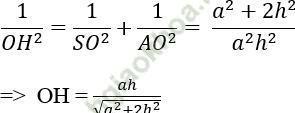
Chọn đáp án D
Câu 3: Cho hình chóp S. ABCD có mặt đáy ABCD là hình chữ nhật với AB = a; AD = 2a và SA vuông góc với mặt đáy và SA = a. Tính khoảng cách giữa SA và BD theo a?
Kẻ AH vuông góc BD tại H.
Do SA ⊥ (ABCD) và AH ⊂ (ABCD) nên SA ⊥ AH
⇒ AH là đoạn vuông góc chung của SA và BD.
Nên: d (SA; BD) = AH
Xét tam giác ABD vuông tại A đường cao AH có:
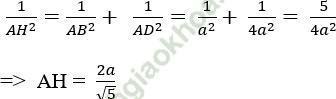
Chọn đáp án D
Câu 4: Cho hình hộp chữ nhật ABCD. A1B1C1D1 có AA1 = 2a; AD = 4a. Gọi M là trung điểm AD. Khoảng cách giữa hai đường thẳng A1B1 và C1M bằng bao nhiêu?
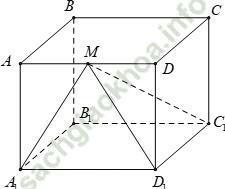
+ Ta có A1B1 // C1D1 suy ra d (A1B1, C1M) = d (A1B1, (C1D1M)) = d (A1, (C1D1M))
+ Vì AA1 = 2a; AD = 4a và M là trung điểm AD nên hai tam giác AMA1 và MDD1 là tam giác vuông cân
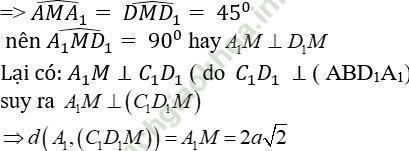
Chọn đáp án B
Câu 5: Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh a. Biết hai mặt bên (SAB) và (SAD) cùng vuông góc với mặt phẳng đáy và SA = a√ 2. Khoảng cách giữa AD và SB là
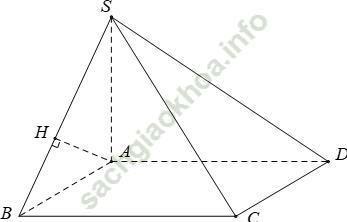
+ Vì hai mặt bên (SAB) và (SAD) cùng vuông góc với mặt phẳng đáy, mà (SAB) ∩ (SAD) = SA nên SA ⊥ (ABCD)
+ Ta có:
AD ⊥ SA (vì SA vuông góc với đáy)
AD ⊥ AB (vì ABCD là hình vuông).
Mà SA và AB ⊂ (SAB)
⇒ AD ⊥ (SAB) tại A.
Trong mp (SAB); dựng AH ⊥ SB
⇒ AH là đoạn vuông góc chung của SB và AD.
Ta tính AH: Xét tam giác SAB vuông tại A có:
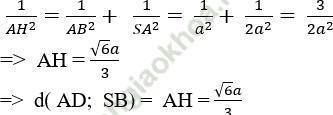
Chọn đáp án C
Câu 6: Cho hình chóp S. ABCD có đáy là hình thang vuông tại A và B; AB = BC = a; AD = 2a; SA vuông góc với mặt đáy và SA = a. Tính khoảng cách giữa AD và SB?
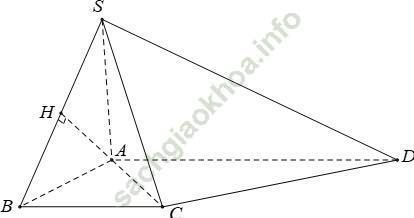
Ta có:
AD ⊥ SA (vì SA vuông góc với đáy)
AD ⊥ AB (vì ABCD là hình thang vuông tại A và B)
Mà SA và AB ⊂ (SAB)
⇒ AD ⊥ (SAB) tại A.
Trong (SAB) dựng AH ⊥ SB
⇒ SH là đoạn vuông góc chung của SB và AD
Ta có:
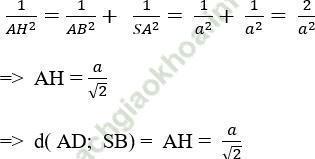
Chọn đáp án D
Câu 7: Cho hình lập phương ABCD. A’B’C’D’. Đoạn vuông góc chung của hai đường thẳng chéo nhau AD và A’C’ là:
A. AA’
B. BB’
C. DA’
D. DD’
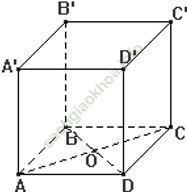
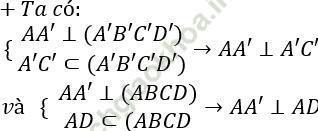
Vậy đoạn vuông góc chung của AD và A’C’ là AA’
Chọn đáp án A.