Phương trình bậc nhất đối với hàm số lượng giác - Chuyên đề Toán 11
A. Phương pháp giải
+ Định nghĩa: Phương trình bậc nhất đối với một hàm số lượng giác là có dạng:
a. sinx + b= 0 (trong đó a ≠ 0) hoặc (a. cosx+b= 0; a. tan x+ b= 0; a. cotx+ b= 0)
+ Để giải được phương trình bậc nhất đối với một hàm số lượng giác ta làm như sau:
• Bước 1: Đưa phương trình về dạng: sinx = m (hoặc cosx = m; tanx = m; cotx = m).
• Bước 2. Giải phương trình lượng giác cơ bản.
• Bước 3. Kết luận nghiệm của phương trình đã cho.
B. Ví dụ minh họa
Ví dụ 1. Nghiệm của phương trình √ 12 + 2tanx = 0 là:
A. π/6 + kπ
B. (-π)/3 + kπ
C. (-π)/6 + kπ
D. (-π)/6 + k2π
Bài giải:
Đáp án đúng là: C
Hướng dẫn:
Ta có: √ 12+2tanx=0 ⇔ 2√ 3+2tanx=0
⇔ tan x= - √ 3 ⇔ tanx= tan (- π)/3
⇔ x= (-π)/3+kπ
Ví dụ 2. Tìm nghiệm của phương trình:
A. 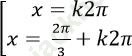
B. 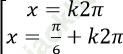
C. 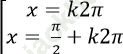
D.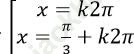
Bài giải:
Đáp án đúng là: A.
Hướng dẫn:
Ta có:
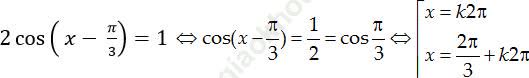
Ví dụ 3. Cho phương trình: ![]() . Tìm m để phương trình có nghiệm?
. Tìm m để phương trình có nghiệm?
A. Không tồn tại m.
B. m ϵ [-1; 3].
C. m ϵ [-3; -1]
D. mọi giá trị của m.
Bài giải:
Đáp án đúng là: C.
Ta có:
Với mọi x ta luôn có: - 1 ≤ cos (2x- π/3) ≤ 1
Do đó phương trình có nghiệm khi và chỉ khi:
-1 ≤ m+2 ≤ 1 hay-3 ≤ m ≤ -1
Ví dụ 4: Họ nghiệm của phương trình cot (x+π/3)+1=0 là
A. ![]()
B. ![]()
C.![]()
D. ![]()
Bài giải:
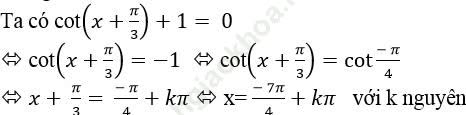
Ví dụ 5: Nghiệm của phương trình 3cot x + √ 3 = 0 là:
A. ![]()
B. ![]()
C. ![]()
D. x = (-π)/3+kπ.
Bài giải:
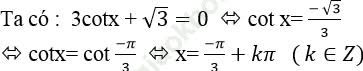
Ví dụ 6: Phương trình ![]() có nghiệm là
có nghiệm là
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Bài giải:
Đáp án đúng là: B.
Hướng dẫn:
Ta có: √ 3+tanx=0
Ví dụ 7: Giải phương trình: 2tanx + 10 = 0
A. x = arctan 5 + k. π
B. x = arctan - 5 + kπ
C. x = - 5 + kπ
D. x = 1/5 + kπ
Bài giải:
Ta có: 2tanx + 10 = 0
⇒ 2tanx = - 10
⇒ tanx = - 5.
Sử dụng công thức nghiệm tổng quát của phương trình
Suy ra: Nghiệm của phương trình đã cho là: x = arctan - 5 + kπ; k∈Z
Ví dụ 8: Giải phương trình: 1/2. cot (x + 3π/4) = 0.
A. (-π)/4 + kπ.
B. π/4 + kπ.
C. π/2 + kπ.
D. π/3 + kπ
Bài giải:
Đáp án đúng là: A.
Hướng dẫn:
Ta có: 1/2. cot (x + 3π/4) = 0
⇒ cot (x + 3π/4) = 0.
⇒ cot (x+ 3π/4) = cot π/2
⇒ x + 3π/4 = π/2 + kπ
⇒ x = (-π)/4 + kπ
Ví dụ 9: Nghiệm của phương trình: ![]()
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Bài giải:
Đáp án đúng là: D.
Ví dụ 10. Giải phương trình: 2cos (x + 300) + 1 = 0
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Bài giải:
Đáp án đúng là: B.
Hướng dẫn:
Ta có: 2cos (x + 300) + 1 = 0
⇒ 2cos (x + 300) = - 1
⇒ cos (x + 300) = -1/2 = cos1200
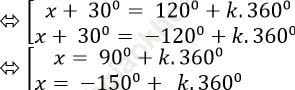
Ví dụ 11: Giải phương trình: 2sin (x – 100) – sin900 = 0
A.![]()
B. ![]()
C. ![]()
D. Một đáp án khác
Bài giải:
Đáp án đúng là: C.
Hướng dẫn:
Ta có: 2sin (x - 100) - sin 900= 0
⇒ 2sin (x – 100) = sin900 = 1
⇒ sin (x - 100) = 1/2 = sin300
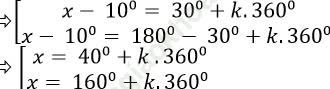
Ví dụ 12. Giải phương trình 2cos (x + 100) + 10 = 0
Bài giải:
Ta có: 2cos (x+ 100) + 10 = 0
⇒ 2cos (x + 100) = - 10
⇒ cos (x + 100) = - 5 (*)
Do với mọi x ta luôn có: - 1 ≤ cos (x+ 100) ≤ 1 nên từ (*) suy ra phương trình (*) vô nghiệm.
Vậy phương trình đã cho vô nghiệm.
C. Bài tập vận dụng
Câu 1: Giải phương trình 2cos (1200 - x) + 1 = 0
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Ta có: 2cos (1200- x) + 1 = 0
⇒ 2cos (1200 – x) = - 1
⇒ cos (1200-x) = (- 1)/2=cos1200
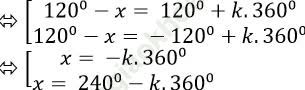
Vậy phương trình đã cho có nghiệm là:
Câu 2: Giải phương trình: 3sin (x- π/5)+3=0
Ta có:
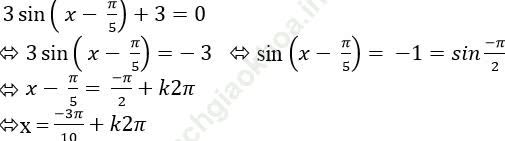
Chọn C.
Câu 3:Giải phương trình: √ 2 tan (x- 150)- √ 2=0
A. 300+ k. 1800
B. 450+ k. 3600
C. 450+ k. 1800
D. 600+ k. 1800
Lời giải
Ta có: √ 2 tan (x- 150)- √ 2=0
⇒ √ 2 tan (x- 150)= √ 2
⇒ tan (x- 150) = 1= tan 450
⇒ x- 150 = 450+ k. 1800
⇒ x = 600+ k. 1800
Vậy nghiệm của phương trình đã cho là x= 600+ k. 1800
Chọn D.
Câu 4: Giải phương trình 3 cot (x+ 2π/5)- √ 3=0
A.
B.
C.
D.
Ta có:
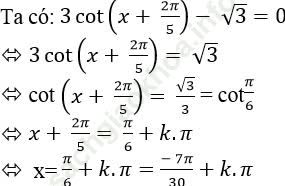
Chọn B.
Câu 5: Giải phương trình 2tanx – 6= 0
A. x= 3+ k. π
B. x = - 3+ kπ
C. x= arctan 3+ kπ
D. Phương trình vô nghiệm
Ta có: 2tanx – 6= 0 ⇒ 2tanx = 6
⇒ tan x= 3
⇒ x = arcrtan 3+ k. π
Chọn C.
Câu 6: Giải phương trình
A.
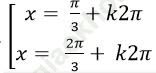
B.
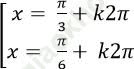
C.
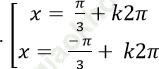
D. Phương trình vô nghiệm
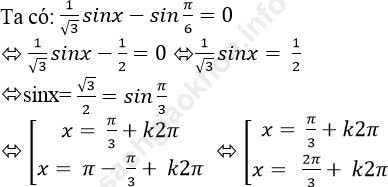
Chọn A.
Câu 7:Giải phương trình 3sin (x+ 100) - 1=0
A.

B.
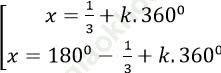
C.
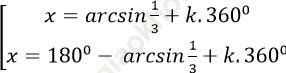
D.

Ta có; 3sin (x+ 100) - 1= 0
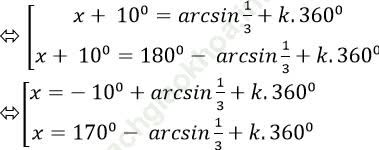
Chọn D.
Câu 8:Giải phương trình √ 3 sin (x+π/10)+3=0
A. x= π/10+k2π
B. x= -π/10+k2π
C. Phương trình vô nghiệm
D. Đáp án khác
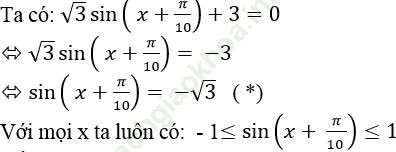
Kết hợp với (*) suy ra phương trình đã cho vô nghiệm
Chọn D.
Câu 9:Giải phương trình: 2sin (x+π/6) – cos 3π/2=0
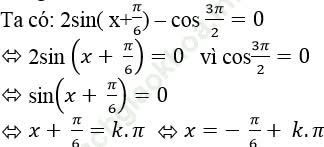
Chọn A.
Câu 10:Giải phương trình: 2sin (x+ π/8)-10=0
A.
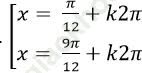
B.
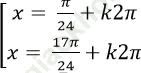
C.
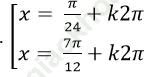
D.
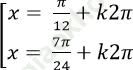
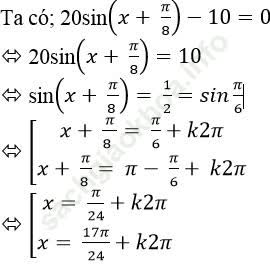
Chọn B.