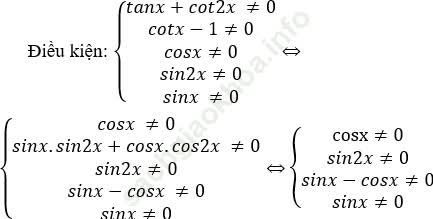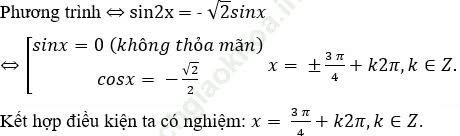Dạng 8: Phương pháp loại nghiệm, hợp nghiệm trong phương trình lượng giác - Chuyên đề Toán 11

Phương pháp loại nghiệm, hợp nghiệm trong phương trình lượng giác

A. Phương pháp giải & Ví dụ

Phương pháp 1: Biểu diễn các nghiệm và điều kiện lên đưòng tròn lượng giác. Ta loại đi những điểm biểu diễn của nghiệm mà trùng với điểm biểu diễn của điều kiện.

Khi áp dụng cách này cần ghi nhớ:

♦ Điểm biểu diễn cung α và α+k2π, k ∈ Z là trùng nhau

♦ Để biểu diễn cung α+k2π /n lên đường tròn lượng giác ta cho k nhận n giá trị (thường chọn k = 0,1,2, …, n – 1)) nên ta có được n điểm phân biệt cách đều nhau trên đường tròn tạo thành một đa giác đều n cạnh nội tiếp đường tròn.

Phương pháp 2: Sử dụng phương trình nghiệm nguyên

Giả sử ta cần đối chiếu hai họ nghiệm , trong đó m, n ∈ Z đã biết, còn k, l ∈ Z là các chỉ số chạy.

Ta xét phương trình:

Với a, b, c là các số nguyên.

Trong trường hợp này ta quy về giải phương trình nghiệm nguyên: ax + by = c (1)

Để giải phương trình (1) ta cần lưu ý kết quả sau:

♦ Phương trình (1) có nghiệm ⇔ d = (a, b) là ước của c

♦ Nếu phương trình (1) có nghiệm (x_o,y_o) thì (1) có vô số nghiệm

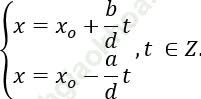
Phương pháp 3: Thử trực tiếp

Phương pháp này là cách đi giải phương trình tìm nghiệm rồi thay nghiệm vào điều kiện để kiểm tra.

Ví dụ minh họa

Bài 1: Giải phương trình: cot3x = cotx

cot3x = cotx

⇔ cos3x. sinx - sin3x. cosx = 0

⇔ sin2x = 0

⇔ x = (k π)/2, k ∈ Z.

Biểu diễn các nghiệm của hệ phương trình điều kiện và nghiệm của phương trình lên vòng tròn lượng giác ta được:

Cách 1: Biểu diễn các điểm cuối của cung kπ /3 ta có các điểm A₁, A₂, A₃, A₄, A₅, A₆.

Biểu diễn các điểm cuối của cung nπ /2 ta có các điểm B₁, B₂, B₃, B₄.

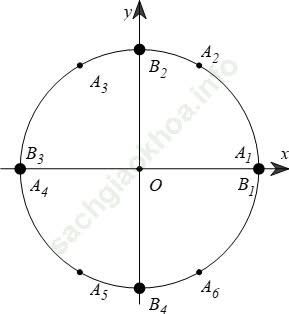
Ta thấy A₁ ≡ B₁, A₄ ≡ B₃.

Vậy nghiệm của phương trình đã cho là: x= π /2 + mπ.

Cách 2:

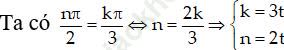
=> Ta cần loại những giá trị n chẵn.

Vậy nghiệm của phương trình là: x = π /2 + mπ.

Bài 2: Giải phương trình: cot4x. cot7x = 1

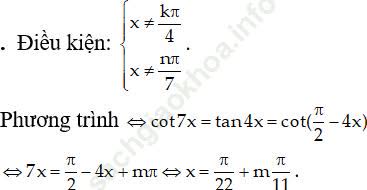
Do: 22n-14m là số chẵn còn 7 là số lẻ nên phương trình này vô nghiệm.

Vậy nghiệm của phương trình đã cho là:

B. Bài tập vận dụng

Bài 1: Giải phương trình: |sinx| = cos2x.

Bài giải:

Với sinx ≥ 0 (*) thì phương trình đã cho tương đương với

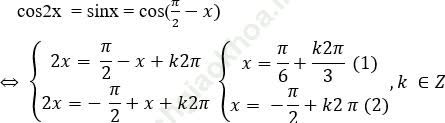
Dễ thấy nghiệm (2) không thỏa (*)

Biểu diễn nghiệm (1) lên đường tròn lượng giác ta được các điểm A1, A2, A3. Trong đó chỉ có hai điểm A1, A2 nằm phía trên Ox.

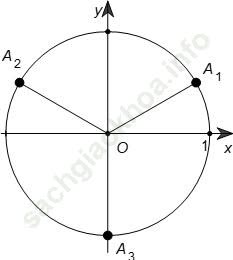
Hai điểm này ứng với các cung x = π /6 + k2 π, x = 5π /6 + k2 π.

Với sinx < 0 (**) thì phương trình đã cho tương đương với:

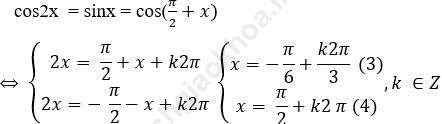
Ta thấy (3) không thỏa (**)

Biểu diễn (4) trên đường tròn lượng giác ta được các điểm B1, B2, B3. Trong đó chỉ có hai điểm B2, B3 nằm dưới Ox (sinx < 0)

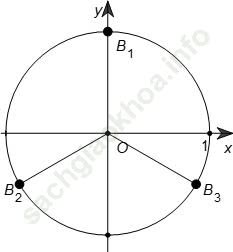
Hai điểm đó ứng với cung: x = (-π)/6 + k2 π, x = -5π /6 + k2 π.

Vậy nghiệm của phương trình đã cho là: x = ±π /6 + k π, (k ∈ Z).

Bài 2: Giải phương trình: cos3x. tan4x = sin5x.

Bài giải:

Điều kiện: cos4x ≠ 0

Ta có: cos3x. tan4x = sin5x.

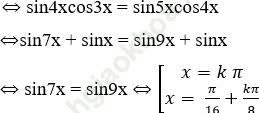
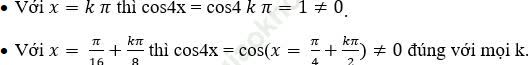
Bài 3: Giải phương trình: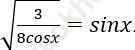

Bài giải:

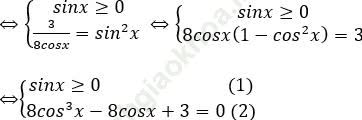
Giải phương trình (2) ta có các nghiệm:

Vì các nghiệm của phương trình phải thỏa điều kiện (1) nên ta tìm cách biểu diễn các nghiệm qua sinx.

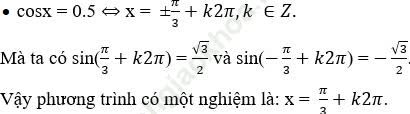
Bài 4: Giải phương trình: tanx + cotx = 2.

Bài giải:

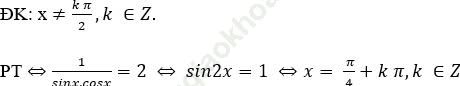
Biểu diễn các điểm trên vòng tròn lượng giác:

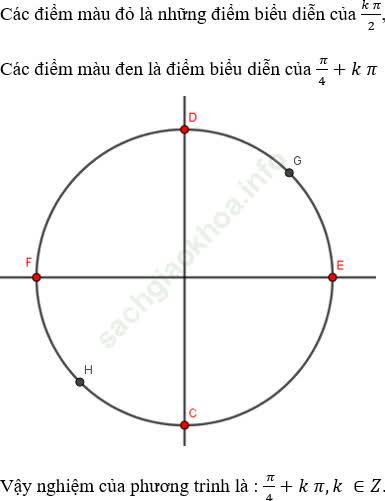
Bài 5: Giải phương trình:

Bài giải: