Cách xét tính đơn điệu của dãy số cực hay có lời giải - Chuyên đề Toán 11

A. Phương pháp giải

* Định nghĩa:

+ Dãy số (u_n) được gọi là dãy số tăng nếu với mọi n ta có u_n < u_{n + 1}

+ Dãy số (u_n) được gọi là dãy số giảm nếu với mọi n ta có: u_n > u_n+1

* Để xét tính tăng (giảm) của dãy số ta có 2 cách sau:

+ Cách 1: Xét hiệu: u_n+1 − u_n

Nếu u_n+1 − u_n > 0 thì dãy số tăng.

Nếu u_n+1 − u_n < 0 thì dãy số giảm

+ Cách 2. Nếu các số hạng của dãy u_n > 0 với mọi n: Xét thương

Nếu T > 1 thì dãy số tăng.

Nếu T < 1 thì dãy số giảm.

B. Ví dụ minh họa

Ví dụ 1: Cho dãy số (u_n) với u_n = a. 10ⁿ (với a hằng số).Khẳng định nào sau đây là sai?

A. Dãy số có u_n+1 = a. 10ⁿ⁺¹.

B. Hiệu số u_n+1 − u_u = 10a.

C. Với a > 0 thì dãy số tăng

D. Với a < 0 thì dãy số giảm.

Bài giải:

+Ta có: u_n+1 = a. 10^{n + 1}

+ Xét hiệu: u_n+1 − u_n = a. 10ⁿ⁺¹ − a. 10ⁿ = a. 10ⁿ (10 − 1) = 9a. 10ⁿ.

+ Nếu a > 0 thì u_{n + 1} − u_n > 0 nên dãy số tăng.

Và nếu a < 0 thì u_{n + 1} − u_n < 0 nên dãy số giảm.

=> B sai

Chọn B.

Ví dụ 2: Cho dãy số (u_n) với (a là hằng số). Khẳng định nào sau đây là đúng?

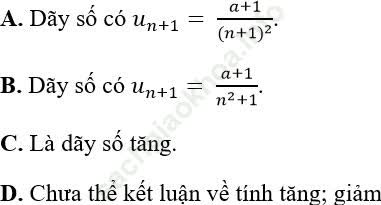
Bài giải:

+ Ta có:

+ Xét hiệu:

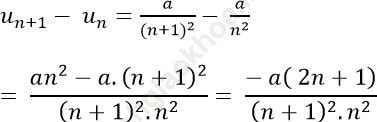
Nếu a > 0 thì u_{n + 1} − u_n < 0 => Dãy số giảm

Nếu a < 0 thì u_n+1 − u_n > 0 => dãy số tăng

Do chưa biết dấu của a nên ta chưa thể kết luận tính tăng; giảm của dãy số.

Khẳng định đúng là: D.

Ví dụ 3: Cho dãy số (u_n) với (k là hằng số). Khẳng định nào sau đây là sai?

Bài giải:

+ Số hạng thứ 4 của dãy số là

+ Số hạng thứ n + 1 của dãy số là

+ Xét hiệu:

=> Nếu k > 0 thì T < 0 nên dãy số giảm

Nếu k < 0 thì T > 0 nên dãy số tăng

=> B sai.

Khẳng định sai là: B.

Ví dụ 4: Cho dãy số (u_n) với . Khẳng định nào sau đây là sai?

Bài giải:

+ Số hạng thứ 9 của dãy số là:

+ Số hạng thứ 10 của dãy số là:

+ Số hạng thứ 5 của dãy số là:

+ Dãy u_n là một dãy đan dấu nên đây là dãy số không tăng; không giảm

=> C sai.

Khẳng định sai là: C.

Ví dụ 5: Cho dãy số (u_n) có u_n = − n² + n + 1. Khẳng định nào sau đây là đúng?

A. 5 số hạng đầu của dãy là − 1; 1; − 5; − 11; − 19.

B. Số hạng thứ n+1 là: u_n+1 = − n² + n + 2.

C. Số hạng thứ 10 của dãy số là: u₁₀ = 89

D. Là một dãy số giảm.

Bài giải:

Ta xét các phương án:

+ 5 số hạng đầu tiên của dãy số là: 1; − 1; − 5; − 11; − 19

+ Số hạng thứ n+ 1 của dãy số là u_{n + 1} = − (n+1)² + (n+1) + 1 = − n2 − n + 1

+ Số hạng thứ 10 của dãy số là: u₁₀ = − 89

+ Xét hiệu T = u_n+1 − u_n = (− n² − n + 1) − (− n² + n + 1)= − 2n < 0 với ∀ n ≥ 1

Do đó (u_n) là một dãy giảm.

Khẳng định đúng là: D.

Ví dụ 6: Cho dãy số (u_n) với . Khẳng định nào sau đây là sai?

Bài giải:

+ Ta có:

+ Xét hiệu:

=> u_n+1 > u_n và dãy số đã cho là dãy số tăng.

=> B sai.

Khẳng định sai là: B.

Ví dụ 7: Xét tính tăng; giảm của dãy số (u_n) biết

A. Dãy số giảm

B. Dãy số tăng

C. Dãy số không tăng; không giảm

D. Đáp án khác

Bài giải:

Số hạng thứ n+1 là

+ Xét hiệu:

∀ n ∈ N*

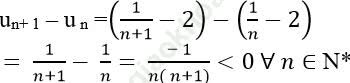
=> Dãy số (u_n) là dãy số giảm.

Đáp án đúng là: A.

Ví dụ 8: Chọn mệnh đề sai. Cho dãy số (u_n) xác định bởi

Bài giải:

Ta có:

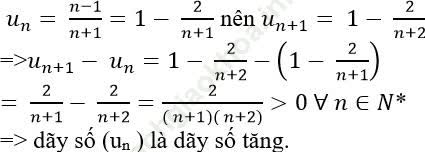
Khẳng định sai là: C.

Ví dụ 9: Cho dãy số (u_n) xác định bởi: u_n = (− 1)ⁿ. (2ⁿ + 1). Tìm mệnh đề sai.

A. u₁ = − 3

B. u₂ = 5

C. Dãy số giảm

D. Dãy số không tăng; không giảm

Bài giải:

Ta có: u₁ = − 3; u₂ = 5; u₃ = − 9

Từ đó suy ra dãy số (u_n) là dãy số không tăng; không giảm.

=> C sai.

Mệnh đề sai là: C.

C. Bài tập trắc nghiệm

Câu 1: Cho dãy số (u_n) xác định bởi . Tìm mệnh đề sai?

Hiển thị đáp án

Đáp án: C

+ Do n ∈ N* nên u_n > 0 với mọi n.

Xét tỉ số:

=> u_n < u_{n + 1}

=> Dãy số (u_n) là một dãy số tăng.

=> C sai

Câu 2: Cho dãy số (un) xác định bởi u_n = 2n − √ (4n² − 1). Tìm mệnh đề sai?

Hiển thị đáp án

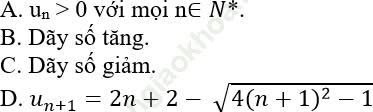
Đáp án: B

+ Ta có:

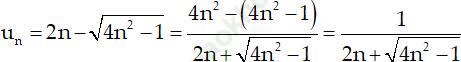
=> u_n > 0 với mọi n ∈ N*.

+ Lại có: u_n+1 = 2n+2 − √ (4 (n+1)² − 1)

+ Xét hiệu:

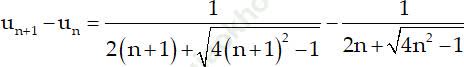
∀ n ∈ N*

Vì:

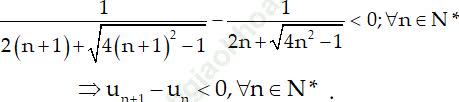
Vậy: dãy số (u_n) giảm.

=> B sai

Câu 3: Cho dãy số (u_n) xác định bởi:

. Chọn mệnh đề sai.

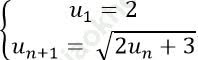
A. Dãy số tăng.

B. Dãy số giảm

C. Số hạng thứ 2 là u₂ = √ 7.

D. u_n > 1 với mọi n.

Hiển thị đáp án

Đáp án: B

+ Ta có: u₂ = √ (2u₁ + 3) = √ 7 > u₁

+ Ta dự đoán u_n+1 > u_n (*) với mọi n ≥ 1. Ta chứng minh (*) bằng phương pháp quy nạp.

Ta có (*) đúng với n = 1

Giả sử ta có: u_k > u_{k − 1} với k ≥ 2. Khi đó ta có:

u_k+1 = √ (2u_k + 3) > √ (2u_{k− 1} + 3) = u_k (do u_k > u_{k − 1})

Suy ra (*) đúng với mọi n ∈ N*.

Vậy (u_n) là dãy số tăng.

=> B sai.

Câu 4: Cho dãy số (u_n) xác định bởi: 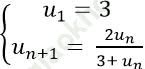. Chọn mệnh đề sai.

A. Số hạng thứ hai u₂ = 1.

B. Dãy số (u_n) giảm.

C. Dãy số (u_n) tăng.

D. Các số hạng của dãy luôn dương.

Hiển thị đáp án

Đáp án: C

* Từ hệ thức truy hồi đã cho; ta chứng minh u_n > 0 với mọi n.

Thật vậy; u₁ = 3 > 0

=> đúng với n = 1.

Giả sử đúng với n = k và k ∈ N*; tức là u_k > 0

Ta chứng minh u_k+1 > 0.

Thật vậy;

mà u_k > 0 nên u_{k + 1} > 0.

*Ta có:

Ta dự đoán u_{n + 1} < u_n (**) với mọi n ∈ N*.

Ta có (**) đúng khi n = 1. Giả sử có u_k < u_k-1

Khi đó

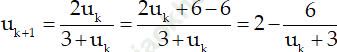
Vì u_k < u_{k− 1} nên

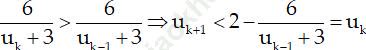
Suy ra (**) đúng với mọi n.

Vậy (u_n) là dãy số giảm.

=> C sai.

Câu 5: Cho a dãy số (u_n) xác định bởi: u_n = 2n³ − 5n + 1. Tìm mệnh đề đúng

A. Dãy số tăng.

B. Dãy số giảm.

C. Số hạng thứ n+1 là u_{n + 1} = 2 (n+1)³ − 5n + 1

D. Dãy số không tăng không giảm.

Hiển thị đáp án

Đáp án: A

Dãy số (u_n) với u_n = 2n³ − 5n + 1

Với mỗi n, ta có: u_n+1 − u_n = [2. (n+1)³ − 5 (n+1)+ 1] − (2n³ − 5n+1)

= 2n3 + 6n2 + 6n+ 2- 5n – 5+ 1 – 2n3 + 5n – 1

= 6n2 + 6n – 3= 6n2 + 3n+ (3n- 3)> 0 đúng do n≥1

Vì thế dãy số (un) là một dãy số tăng.

=> A đúng.

Chọn A.

Câu 6: Cho dãy số (u_n) xác định bởi u_n = 3ⁿ − n và dãy số (v_n) xác định bởi

. Tìm mệnh đề đúng?

A. Dãy số (u_n) và (v_n) là hai số tăng.

B. Dãy số (u_n) và (v_n) là hai dãy số giảm.

C. Dãy số (u_n) tăng và dãy số (v_n) là giảm

D. Dãy số (u_n) giảm và dãy số (v_n) là tăng.

Hiển thị đáp án

Đáp án: C

* Xét dãy số (u_n) với u_n = 3ⁿ − n.

Với mỗi n ∈ N*, ta có: u_n+1 − u_n = [3ⁿ⁺¹ − (n + 1)] − (3ⁿ − n)

= 3.3ⁿ − n − 1 − 3ⁿ + n= 2.3ⁿ − 1 > 0 vì n ∈ N*

=> Dãy số (u_n) là dãy số tăng.

* Xét dãy số (v_n) với

.

Với mỗi n ∈ N* ta có:

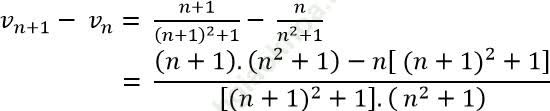
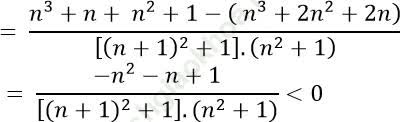
Vì (− n² − n + 1) < 0 với ∀ n ≥ 1, và [(n+1)² + 1]. (n² + 1) > 0

Kết luận: dãy số (v_n) là một dãy số giảm.

Câu 7: Cho dãy số (un) với

và dãy số (vn) với . Tìm mệnh đề đúng?

A. Dãy số (u_n) tăng; dãy số (v_n) giảm.

B. Dãy số (u_n)giảm; dãy số (v_n) tăng.

C. Dãy số (u_n) và (v_n) đều giảm.

D. Dãy số (u_n) và (v_n) đều tăng.

Hiển thị đáp án

Đáp án: B

* Xét dãy số (u_n) với

Dễ thấy un > 0 với mọi n. Xét tỉ số

Ta có:

Thật vậy:

(luôn đúng với n ≥ 1)

Kết luận: (u_n) là một dãy số giảm.

* Xét dãy số (v_n) với

Ta có:

Với mọi n ∈ N* ta có:

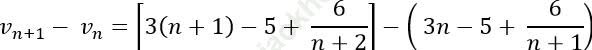
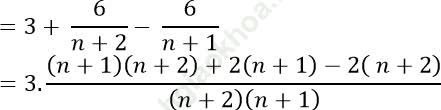
Kết luận (v_n) là dãy số tăng.

Câu 8: Dãy số (u_n) với u_n = n − √ (n² − 1) và dãy số

. Chọn mệnh đề đúng

A. Cả hai dãy số giảm.

B. Cả hai dãy số tăng.

C. Dãy số (u_n) tăng và (v_n) giảm.

D. Dãy số (u_n) giảm và (v_n) tăng.

Hiển thị đáp án

Đáp án: B

* Xét dãy số (u_n) với u_n = n − √ (n² − 1)

Ta có:

Dễ dàng ta có:

hay u_{n + 1} < u_n

Từ đó suy ra dãy số (u_n) là dãy số giảm.

* Xét dãy số (v_n) với

Ta có:

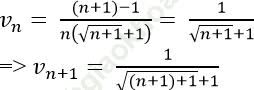
Dễ dàng ta có:

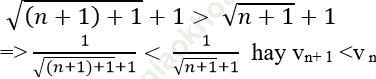
Vậy dãy số (v_n) là dãy số giảm.

Câu 9: Xét tính tăng giảm của các dãy số sau:

A. Dãy số tăng B. Dãy số giảm

C. Dãy số không tăng không giảm D. Cả A, B, C đều sai

Hiển thị đáp án

Đáp án: A

Ta có:

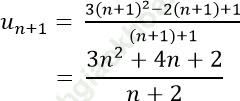
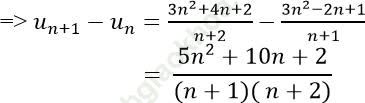
Với ∀ n ∈ N* ta có:

nên u_n+1 − u_n > 0

=> dãy (u_n) là dãy tăng.

Câu 10: Cho dãy số (u_n) với

. Tìm a để dãy số đã cho là dãy số tăng.

A. a < 2 B. a > − 2 C. a < 4 D. a < − 4

Hiển thị đáp án

Đáp án: D

Ta có dãy số (u_n) tăng khi và chỉ khi: u_n+1 − u_n > 0

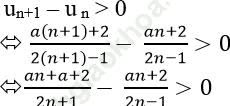
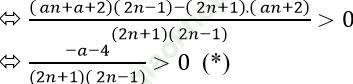
Với n ∈ N* thì (2n+1) > 0 và (2n − 1) < 0 nên (*) chỉ xảy ra khi và chỉ khi: − a − 4 > 0 ⇔ a < − 4

Câu 11: Cho dãy số (u_n) xác định bởi:

. Tìm a để dãy số (u_n) tăng.

Hiển thị đáp án

Đáp án: C

Ta có:

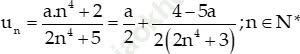
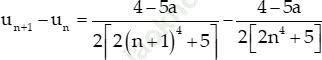
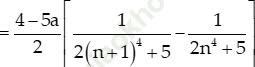
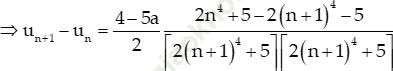
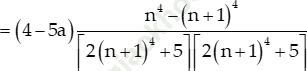
Mà:

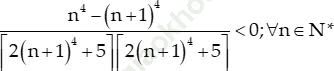
Nên (u_n) tăng ⇔ u_n+1 − u_n > 0 ⇔ 4 − 5a < 0

Bài trước: Cách tìm công thức của số hạng tổng quát cực hay có lời giải - Chuyên đề Toán 11 Bài tiếp: Cách xét tính bị chặn của dãy số cực hay có lời giải - Chuyên đề Toán 11