Dạng 5: Phương pháp giải bài tập Cấp số nhân - Chuyên đề Toán 11

A. Phương pháp giải & Ví dụ

Để xác định một cấp số nhân, ta cần xác định số hạng đầu và công bội. Do đó, ta thường biểu diễn giả thiết của bài toán qua u₁ và q.

Số hạng tổng quát của cấp số nhân: u_n = u₁.q^n-1, n ≥ 1.

Trong đó q: công bội của cấp số nhân.

Tính chất:

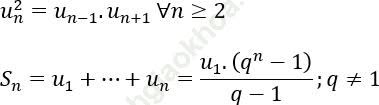
Ví dụ minh họa

Bài 1: Cho cấp số nhân (u_n) có các số hạng khác không, tìm u₁ biết:

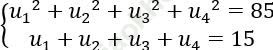
Bài giải:

Ta có:

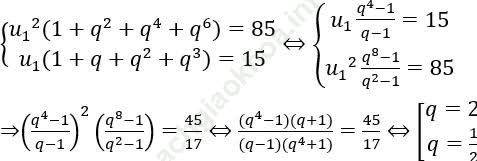
Từ đó ta tìm được u₁=1, u₁=8.

Bài 2: Cho cấp số nhân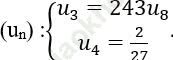

1. Viết 5 số hạng đầu của cấp số;

2. Tính tổng 10 số hạng đầu của cấp số;

3. Số 2/6561 là số hạng thứ bao nhiêu của cấp số?

Bài giải:

Gọi q là công bội của cấp số. Theo giả thiết ta có:

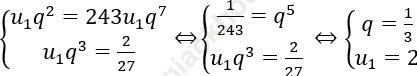
1. Năm số hạng đầu của cấp số là:

u₁ = 2, u₂ = 2/3, u₃ = 2/9, u₄ = 2/27, u₅ = 2/81.

2. Tổng 10 số hạng đầu của cấp số là:

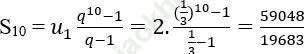
3. Ta có:

Vậy 2/6561 là số hạng thứ 9 của cấp số.

B. Bài tập vận dụng

Bài 1: Cho cấp số nhân (un) có các số hạng khác không, tìm u₁ biết:

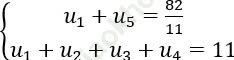
Bài giải:

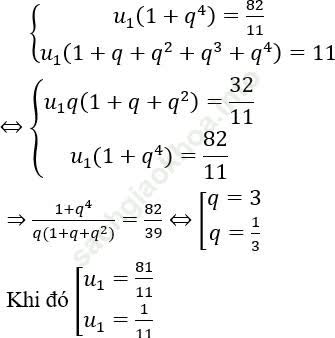
Bài 2: Tìm tổng 5 số hạng đầu tiên của cấp số nhân, biết:

Bài giải:

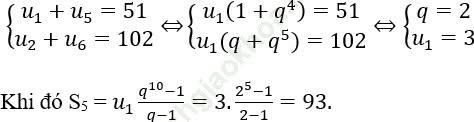
Bài 3: Một cấp số nhân dương có 4 số hạng, công bội q bằng 1/4 lần số hạng thứ nhất, tổng của hai số hạng đầu bằng 24. Tìm tích các số hạng cấp số nhân đó?

Bài giải:

Gọi 4 số lập thành cấp số cộng là u₁,u₂,u₃,u₄

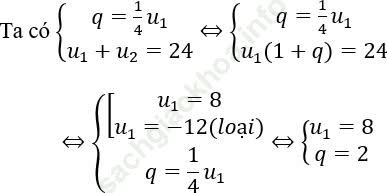
u₁ = 8, u₂ = 16, u₃ = 32, u₄ = 64. Khi đó tích cần tìm là: 8.6.32.64 = 98304.

Bài 4: Cho 4 số nguyên biết rằng 3 số hạng đầu lập thành một cấp số nhân, 3 số hạng sau lập thành một cấp số cộng. Tổng của 2 số hạng đầu và cuối bằng 14, còn tổng 2 số ở giữa bằng 12. Tổng của 4 số nguyên đó là bao nhiêu?

Bài giải:

Gọi 4 số cần tìm là a, b, c, d. Theo giả thiết ta có hệ:

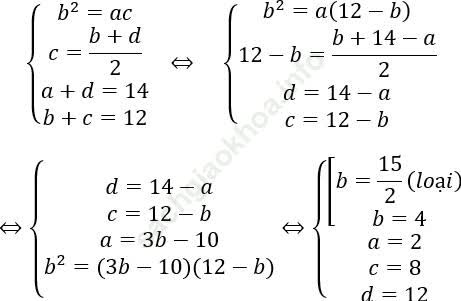
Vậy tổng 4 số nguyên đó là: 2 + 4 + 8 +12 = 26.

Bài 5: Cho cấp số nhân có 7 số hạng, số hạng thứ 4 bằng 6 và số hạng thứ 7 gấp 243 lần số hạng thứ 2. Hãy tìm số hạng còn lại của cấp số nhân đó.

Bài giải:

Từ giả thiết ta có

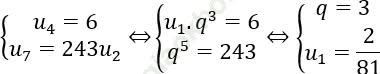
Vậy u₁ = 2/9, u₂ = 2/3, u₃ = 2, u₄ = 6, u₅ = 18, u₆ = 54, u₇ = 162.

Bài trước: Cách chứng minh đẳng thức dựa vào tính chất của cấp số cộng cực hay - Chuyên đề Toán 11