Chứng minh đường thẳng vuông góc với mặt phẳng - Chuyên đề Toán 11
A. Phương pháp giải
* Chứng minh đường thẳng vuông góc với mặt phẳng.
Muốn chứng minh đường thẳng d ⊥ (α) ta có thể dùng 1 trong 3 cách sau:
Cách 1: Chứng minh d vuông góc với hai đường thẳng a; b cắt nhau trong (α).
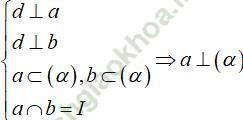
Cách 2: Chứng minh d vuông góc với đường thẳng a mà a vuông góc với (α).
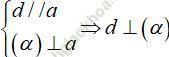
Cách 3: Chứng minh d vuông góc với (Q) và (Q) // (P).
* Chứng minh hai đường thẳng vuông góc
- Để chứng minh d ⊥ a, ta có thể chứng minh bởi 1 trong 3 cách sau:
Cách 1: Chứng minh d vuông góc với (P) và (P) chứa a.
Cách 2: Sử dụng định lí ba đường vuông góc.
Cách 3: Sử dụng các cách chứng minh đã biết ở phần trước.
B. Ví dụ minh họa
Ví dụ 1: Cho hình chóp S. ABC có SA ⊥ (ABC) và ∆ ABC vuông ở B, AH là đường cao của ∆ SAB. Khẳng định nào sau đây sai?
A. SA ⊥ BC
B. AH ⊥ BC
C. AH ⊥ AC
D. AH ⊥ SC
Bài giải:
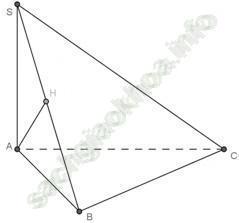
Khẳng định sai là: C
=> C sai.
Ví dụ 2: Cho tứ diện SABC có ABC là ∆ vuông tại B và SA ⊥ (ABC). Khẳng định nào sau đây là đúng nhất.
Bài giải:
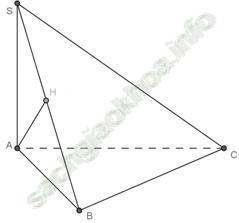
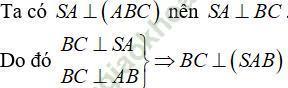
Khẳng định đúng là: A
Ví dụ 3: Cho tứ diện ABCD có AB = AC và DB = DC. Khẳng định nào sau đây đúng?
A. AB ⊥ (ABC)
B. AB ⊥ BD
C. AB ⊥ (ABD)
D. BC ⊥ AD
Bài giải:
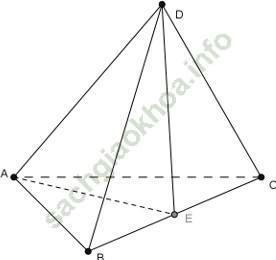
Khẳng định đúng là: D
Gọi E là trung điểm của BC.
∆ DCB cân tại D có DE là đường trung tuyến nên đồng thời là đường cao: DE ⊥ BC.
∆ ABC cân tại A có AE là đường trung tuyến nên đồng thời là đường cao: AE ⊥ BC
Khi đó ta có: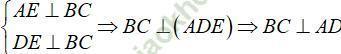 
Ví dụ 4: Cho hình chóp S. ABC có SA ⊥ (ABC) và AB ⊥ BC Số các mặt của tứ diện S. ABC là ∆ vuông là:
A. 1
B. 2
C. 3
D. 4
Bài giải:
Đáp án đúng là: D
Có AB ⊥ BC ⇒ Δ ABC là tam giác vuông tại B
Ta có: SA ⊥ (ABC) ⇒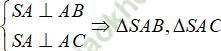 
là các tam giác vuông tại A.
Mặt khác:
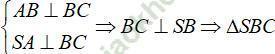là tam giác vuông tại B.
Vậy 4 mặt của tứ diện đều là tam giác vuông. => Đáp án D đúng.
Ví dụ 5: Cho hình chóp S. ABCD có đáy ABCD là hình thoi tâm O. Biết SA = SC và SB = SD. Khẳng định nào sau đây sai?
A. SO ⊥ (ABCD)
B. CD ⊥ (SBD)
C. AB ⊥ (SAC)
D. CD ⊥ AC
Bài giải:
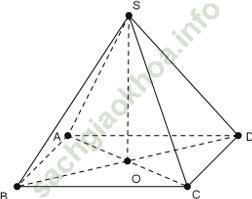
Đáp án đúng là: B
Tam giác SAC cân tại S có SO là trung tuyến nên SO cũng là đường cao ⇒ SO ⊥ AC.
Tam giác SBD cân tại S có SO là trung tuyến nên SO cũng là đường cao ⇒ SO ⊥ BD.
=> SO ⊥ (ABCD).
Do ABCD là hình thoi nên CD không vuông góc với BD. Do đó CD không vuông góc với (SBD)
Ví dụ 6: Cho hình chóp S. ABCD có đáy ABCD là hình chữ nhật, SA ⊥ (ABCD). Gọi AE, AF lần lượt là các đường cao của ∆ SAB và tam giác SAD. Chọn khẳng định đúng trong các khẳng định sau?
Bài giải:
Đáp án đúng là: D
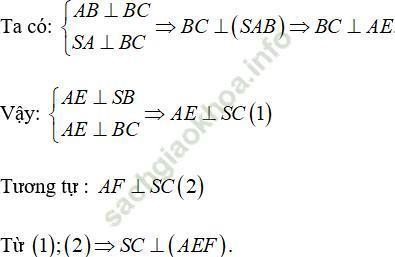
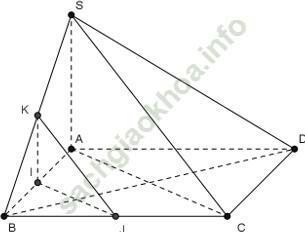
Ví dụ 7: Cho hình chóp S. ABC có cạnh SA ⊥ (ABC) và đáy ABC là ∆ cân ở C. Gọi H và K lần lượt là trung điểm của AB và SB. Khẳng định nào sau đây sai?
A. CH ⊥ SA
B. CH ⊥ SB
C. CH ⊥ AK
D. AK ⊥ SB
Bài giải:
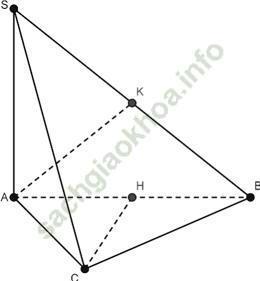
Đáp án đúng là: D
Do ∆ ABC cân tại C; có CH là đường trung tuyến nên đồng thời là đường cao nên CH ⊥ AB.
Lại có: CH ⊥ SA (vì SA vuông góc với mp (ABC)).
=> CH ⊥ (SAB). Vậy các câu A, B, C đúng nên D sai.
Ví dụ 8: Cho tứ diện ABCD. Vẽ AH ⊥ (BCD). Biết H là trực tâm ∆ BCD. Khẳng định nào sau đây đúng?
A. CD ⊥ BD
B. AC = BD
C. AB = CD.
D. AB ⊥ CD
Bài giải:
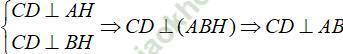
Đáp án đúng: D
Ví dụ 9: Cho tứ diện SABC thoả mãn SA= SB= SC. Gọi H là hình chiếu của S lên mặt phẳng (ABC). Đối với ∆ ABC ta có điểm H là:
A. Trực tâm.
B. Tâm đường tròn nội tiếp.
C. Trọng tâm.
D. Tâm đường tròn ngoại tiếp.
Bài giải:
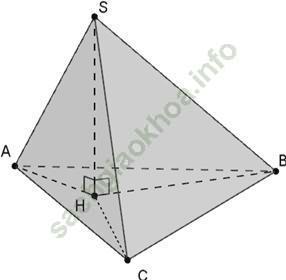
Ví dụ 10: Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau. Gọi H là hình chiếu của O trên mặt phẳng (ABC). Mệnh đề nào sai trong các mệnh đề sau:
A. H là trực tâm ∆ ABC
B. H là tâm đường tròn ngoại tiếp ∆ ABC
C.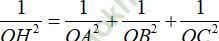 
D. CH là đường cao của ∆ ABC.
Bài giải:
Mệnh đề B sai
+ Ta có OA ⊥ (OBC) ⇒ OA ⊥ BC và OH ⊥ BC ⇒ BC ⊥ (OAH) ⇒ BC ⊥ AH. Tương tự, ta có AB ⊥ CH
Hai đường thẳng AH và CH cắt nhau tại H nên H là trực tâm ∆ ABC
=> Đáp án A, D đúng
+ Gọi I là giao điểm của AH và BC.
Ta có; OA ⊥ (OBC) nên OA ⊥ OI
Xét tam giác vuông OAI có đường cao OH
Ta có:
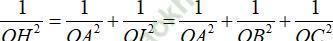
=> Đáp án C đúng.
Ví dụ 11: Cho hình chóp S. ABC có ∠ BSC = 120°, ∠ CSA = 60°, ∠ ASB = 90°, SA = SB = SC. Gọi I là hình chiếu vuông góc của S lên mp (ABC). Chọn khẳng định đúng trong các khẳng định sau
A. I là trung điểm AB
B. I là trọng tâm ∆ ABC
C. I là trung điểm AC
D. I là trung điểm BC
Bài giải:
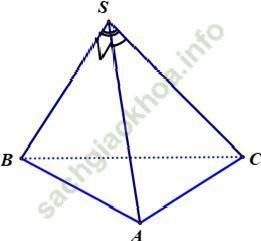
Khẳng định đúng là D
Gọi SA = SB = SC = a
+ Ta có: ∆ SAC đều nên AC = SA = a
∆ SAB vuông cân tại S ⇒ AB = a√ 2
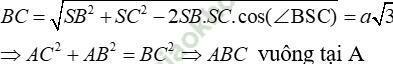
+ Gọi I là trung điểm của BC thì IA = IB = IC nên I là tâm đường tròn ngoại tiếp ∆ ABC.
Ta có: SA = SB = SC và IA = IB = IC
⇒ SI là trục đường tròn ngoại tiếp ∆ ABC
⇒ SI ⊥ (ABC)
Vậy nên I là hình chiếu vuông góc của S lên mặt phẳng (ABC)
C. Bài tập vận dụng
Câu 1: Cho tứ diện ABCD có AB ⊥ CD và AC ⊥ BD. Gọi H là hình chiếu vuông góc của A lên mp (BCD). Các khẳng định sau, khẳng định nào sai?
A. H là trực tâm ∆ BCD
B. CD ⊥ (ABH)
C. AD ⊥ BC
D. Các khẳng định trên đều sai.
Ta có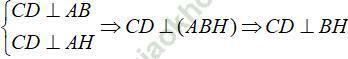 
Tương tự BD ⊥ CH
Suy ra H là trực tâm tam giác BCD. Suy ra loại đáp án A, B
Ta có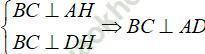 
suy ra loại C.
Chọn đáp án D
Câu 2: Cho hình chóp S. ABC có SA ⊥ (ABC). Gọi H, K lần lượt là trực tâm các ∆ SBC và ABC. Mệnh đề nào sai trong các mệnh đề sau?
A. BC ⊥ (SAH)
B. HK ⊥ (SBC)
C. BC ⊥ (SAB)
D. SH, AK và BC đồng quy
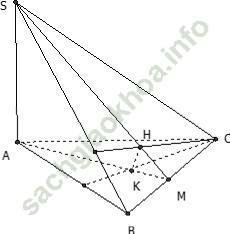
Ta có BC ⊥ SA, BC ⊥ SH ⇒ BC ⊥ (SAH)
Ta có CK ⊥ AB, CK ⊥ SA ⇒ CK ⊥ (SAB) hay CK ⊥ SB
Mặt khác có CH ⊥ SB nên suy ra SB ⊥ (CHK) hay SB ⊥ HK, tương tự SC ⊥ HK nên HK ⊥ (SBC)
Gọi M là giao điểm của SH và BC.
Do BC ⊥ (SAH) ⇒ BC ⊥ AM hay đường thẳng AM trùng với đường thẳng AK
⇒ SH, AK và BC đồng quy
Do dó BC ⊥ (SAB). Sai
Chọn đáp án C
Câu 3: Cho hình chóp S. ABCD có đáy ABCD là hình thoi tâm O. Biết SA = SC và SB = SD. Khẳng định nào sau đây là sai?.
A. SO ⊥ (ABCD)
B. SO ⊥ AC
C. SO ⊥ BD
D. Cả A, B, C đều sai
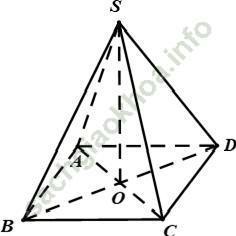
Ta có O là trung điểm của AC và SA = SC ⇒ SO ⊥ AC
Tương tự SO ⊥ BD
Vậy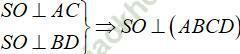 
Chọn D
Câu 4: Cho hình chóp S. ABCD có đáy ABCD là hình thoi tâm O, SA ⊥ (ABCD). Các khẳng định sau, khẳng định nào sai?
A. SA ⊥ BD
B. SC ⊥ BD
C. SO ⊥ BD
D. AD ⊥ SC
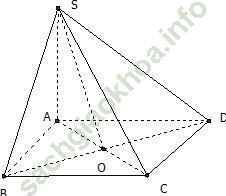
Ta có SA ⊥ (ABCD) ⇒ SA ⊥ BD
Do tứ giác ABCD là hình thoi nên BD ⊥ AC mà SA ⊥ BD nên BD ⊥ (SAC) hay BD ⊥ SC, BD ⊥ SO
Chọn đáp án D
Câu 5: Cho hình chóp S. ABCD có đáy ABCD là hình vuông và SA ⊥ (ABCD). Gọi I; J; K lần lượt là trung điểm của AB, BC và SB. Khẳng định nào sau đây sai?
A. (IJK) // (SAC)
B. BD ⊥ (IJK)
C. Góc giữa SC và BD có số đo 60°
D. BD ⊥ (SAC)
Chọn C.
+ Tam giác ABC có IJ Là đường trung bình của tam giác nên IJ // AC
Tam giác SAB có IK là đường trung bình của tam giác nên IK // SA
⇒ (IJK) // (SAC). Vậy A đúng
+ Do BD ⊥ AC và BD ⊥ SA nên BD ⊥ (SAC)
nên D đúng.
+ Do BD ⊥ (SAC) và (IJK) // (SAC) nên BD ⊥ (IJK) nên B đúng.
Vậy C sai
Câu 6: Cho hình chóp S. ABCD có đáy ABCD là hình vuông, Gọi H là trung điểm của AB và SH ⊥ (ABCD). Gọi K là trung điểm của cạnh AD. Khẳng định nào sau đây là sai?
A. AC ⊥ SH
B. AC ⊥ KH
C. AC ⊥ (SHK)
D. Cả A, B, C đều sai
+ Ta cos SH ⊥ (ABCD) ⇒ SH ⊥ AC
+ Tam giác ABD có H và K lần lượt là trung điểm của AB và AD nên HK là đường trung bình của tam giác ⇒ HK // BD
Lại có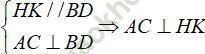 
⇒ AC ⊥ (SHK)
Chọn D
Câu 7: Cho tứ diện OABC có ba cạnh OA; OB; OC đôi một vuông góc. Gọi H là hình chiếu của O lên (ABC). Khẳng định nào sau đây sai?
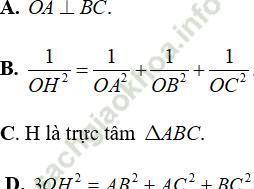
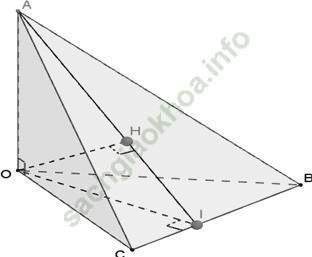
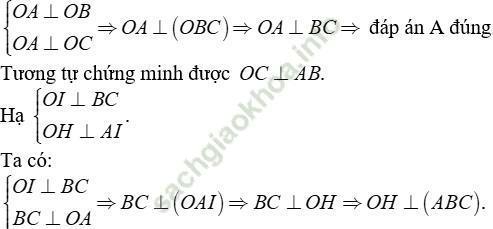
Xét tam giác AOI vuông tại O có OH đường cao:
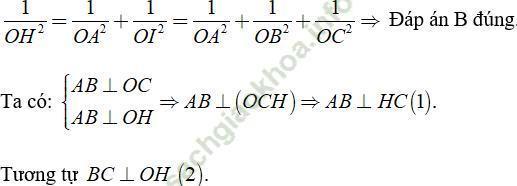
Từ (1) và (2) ⇒ H là trực tâm tam giác ABC ⇒ Đáp án C đúng.
Chọn đáp án D.
Câu 8: Cho hình tứ diện ABCD có AB, BC, CD đôi một vuông góc nhau. Hãy chỉ ra điểm O cách đều bốn điểm A, B; C; D.
A. O là tâm đường tròn ngoại tiếp ∆ ABC
B. O là trọng tâm tam giác ACD
C. O là trung điểm cạnh BD
D. O là trung điểm cạnh AD
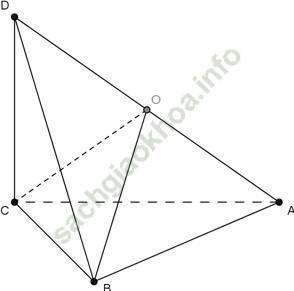
Chọn D
Câu 9: Cho tứ diện ABCD. Vẽ AH ⊥ (BCD). Biết H là trực tâm ∆ BCD. Khẳng định nào sau đây không sai?
A. AB = CD
B. AC = BD
C. AB ⊥ CD
D. CD ⊥ BB
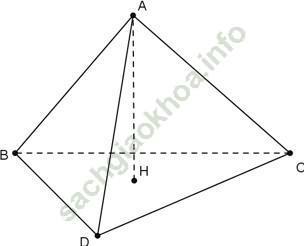
Chọn C
Do AH ⊥ (BCD) ⇒ AH ⊥ CD.
Mặt khác, H là trực tâm tam giác BCD nên BH ⊥ CD
Suy ra CD ⊥ (ABH) nên CD ⊥ AB.
Câu 10: Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh a, mặt bên SAB là ∆ đều và SC = a√ 2. Gọi H, K lần lượt là trung điểm của các cạnh AB và AD. Khẳng định nào sau đây là sai?.
A. SH ⊥ (ABCD)
B. SH ⊥ HC
C. A, B đều đúng
D. A, B là sai
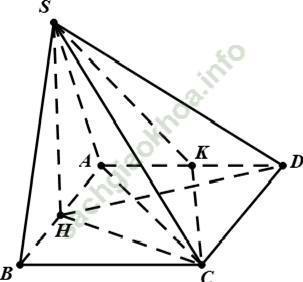
Vì H là trung điểm của AB và tam giác SAB đều nên SH ⊥ AB
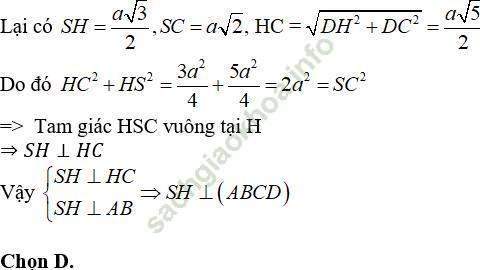
Câu 11: Cho hình lập phương ABCD. A'B'C'D'. Đường thẳng AC’ vuông góc với mặt phẳng nào sau đây?
A. ( A’BD)
B. ( A’DC’)
C. ( A’CD’)
D. ( A’B’CD)
Ta có
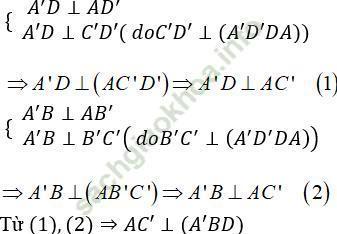
Vậy chọn đáp án A
Câu 12: Cho hình chóp S. ABCD có đáy ABCD là hình thoi, O là giao điểm của 2 đường chéo và SA = SC. Các khẳng định sau, khẳng định nào đúng?
A. SA ⊥ (ABCD)
B. BD ⊥ (SAC)
C. AC ⊥ (SBD)
D. AB ⊥ (SAC)
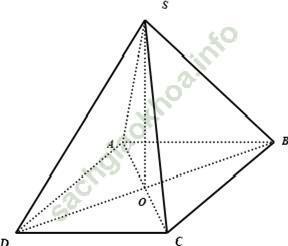
Ta có: SA = SC nên tam giác SAC là tam giác cân
Mặt khác: O là trung điểm của AC (tính chất hình thoi)
Khi đó ta có: AC ⊥ SO
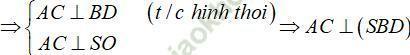
Vậy chọn đáp án C
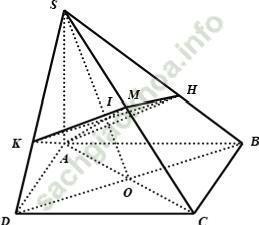
Câu 13: Cho hình chóp S. ABCD có đáy ABCD là hình vuông, SA ⊥ (ABCD). Mặt phẳng qua A và vuông góc với SC cắt SB, SC, SD theo thứ tự tại H, M, K. Chọn khẳng định sai trong các khẳng định sau?
A. AK ⊥ HK
B. HK ⊥ AM
C. BD // KH
D. AH ⊥ SB.
Câu 14: Cho hình chóp S. ABC có ∠ BSC = 120°, ∠ CSA = 60°, ∠ ASB = 90°, SA = SB = SC. Gọi I là hình chiếu vuông góc của S lên mp (ABC). Chọn khẳng định đúng trong các khẳng định sau
A. I là trung điểm AB
B. I là trọng tâm tam giác ABC
C. I là trung điểm AC
D. I là trung điểm BC
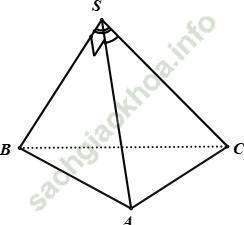
Gọi SA = SB = SC = a
Ta có: tam giác SAC cân có 1 góc bằng 60° nên tam giác SAC đều ⇒ AC = SA = a
+ tam giác SAB vuông cân tại S
⇒ AB = a√ 2
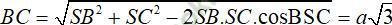
⇒ AC2 + AB2 = BC2 nên tam giác ABC vuông tại A
+ Gọi I là trung điểm của AC thì I là tâm đường tròn ngoại tiếp tam giác ABC. Gọi d là trục của tam giác ABC thì d đi qua I và d ⊥ (ABC)
Mặt khác: SA = SB = SC nên S ∈ d. Vậy SI ⊥ (ABC) nên I là hình chiếu vuông góc của S lên mặt phẳng (ABC)
Chọn C
Câu 15: Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau. Gọi H là hình chiếu của O trên mặt phẳng (ABC). Xét các mệnh đề sau:
I. Vì OC ⊥ OA, OC ⊥ OB nên OC ⊥ (OAB)
II. Do AB ⊂ (ABC) nên AB ⊥ OC (1)
III. Có OH ⊥ (ABC) và AB ⊂ (ABC) nên AB ⊥ OH (2)
IV. Từ (1) và (2) AB ⊥ (OCH)
Trong các mệnh đề trên mệnh đề nào đúng?
A. I, II, III, IV
B. I, II, III
C. II, III, IV
D. I, IV
Ta có:
Chọn đáp án A
Câu 16: Cho hình hộp ABCD. A’B’C’D’ Có đáy là hình thoi ∠ BAD = 60° và AA’ = A’B = A’D. Gọi O = AC ∩ BD. Hình chiếu của A’ trên (ABCD) là:
A. trung điểm của AO
B. trọng tâm tam giác ABD
C. giao của hai đoạn AC và BD
D. trọng tâm tam giác BCD.
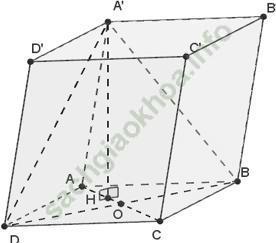
Vì A’A = A’B = A’D nên hình chiếu của A’ trên (ABCD) trùng với H là tâm đường tròn ngoại tiếp tam giác ABD (1).
Mà tứ giá ABCD là hình thoi và ∠ BAD = 60° nên tam giác BAD là tam giác đều (2)
Từ (1) và (2) suy ra H là trọng tâm tam giác ABD
Chọn đáp án B