Dạng 4: Bài toán xếp vị trí, phân công công việc - Chuyên đề Toán 11
A. Phương pháp giải & Ví dụ
Dựa vào hai quy tắc cộng, quy tắc nhân và các khái niệm hoán vị, chỉnh hợp, tổ hợp, đếm gián tiếp, đếm phần bù.
Một số dấu hiệu giúp chúng ta nhận biết được hoán vị, chỉnh hợp hay tổ hợp.
1) Hoán vị: Các dấu hiệu đặc trưng để giúp ta nhận dạng một hoán vị của n phần tử là:
♦ Tất cả n phần tử đều phải có mặt
♦ Mỗi phần tử xuất hiện một lần.
♦ Có thứ tự giữa các phần tử.
2) Chỉnh hợp: Ta sẽ sử dụng khái niệm chỉnh hợp khi
♦ Cần chọn k phần tử từ n phần tử, mỗi phần tử xuất hiện một lần
♦ k phần tử đã cho được sắp xếp thứ tự.
3) Tổ hợp: Ta sử dụng khái niệm tổ hợp khi
♦ Cần chọn k phần tử từ n phần tử, mỗi phần tử xuất hiện một lần
♦ Không quan tâm đến thứ tự k phần tử đã chọn.
Ví dụ minh họa
Bài 1: Đội tuyển học sinh giỏi của một trường gồm 18 em, trong đó có 7 học sinh khối 12,6 học sinh khối 11 và 5 học sinh khối10. Hỏi có bao nhiêu cách cử 8 học sinh đi dự đại hội sao cho mỗi khối có ít nhất 1 học sinh được chọn.
Bài giải:

Bài 2: Một nhóm có 5 nam và 3 nữ. Chọn ra 3 người sao cho trong đó có ít nhất 1 nữ. Hỏi có bao nhiêu cách chọn?
Bài giải:


Bài 3: Trong một môn học, Thầy giáo có 30 câu hỏi khác nhau gồm 5 câu hỏi khó, 10 câu trung bình và 15 câu dễ. Từ 30 câu hỏi đó có thể lập được bao nhiêu đề kiểm tra, mỗi đề gồm 5 câu hỏi khác nhau, sao cho trong mỗi đề nhất thiết phải có đủ cả 3 câu (khó, dễ, Trung bình) và số câu dễ không ít hơn 2?
Bài giải:
Ta có các trường hợp sau:

=> Có tất cả: 56875 đề kiểm tra.
B. Bài tập vận dụng
Bài 1: Hai nhóm người cần mua nền nhà, nhóm thứ nhất có 2 người và họ muốn mua 2 nền kề nhau, nhóm thứ hai có 3 người và họ muốn mua 3 nền kề nhau. Họ tìm được một lô đất chia thành 7 nền đang rao bán (các nền như nhau và chưa có người mua). Tính số cách chọn nền của mỗi người thỏa yêu cầu trên
Bài giải:
Xem lô đất có 4 vị trí gồm 2 vị trí 1 nền, 1 vị trí 2 nền và 1 vị trí 3 nền.
Bước 1: Nhóm thứ nhất chọn 1 vị trí cho 2 nền có 4 cách và mỗi cách có 2! = 2 cách chọn nền cho mỗi người. => Có 4.2 = 8 cách chọn nền.
Bước 2: Nhóm thứ hai chọn 1 trong 3 vị trí còn lại cho 3 nền có 3 cách và mỗi cách có 3! = 6 cách chọn nền cho mỗi người.
=> Có 3.6 = 18 cách chọn nền.
Vậy tất cả có 8.18 = 144 cách chọn nền cho mỗi người
Bài 2: Một nhóm công nhân gồm 15 nam và 5 nữ. Người ta muốn chọn từ nhóm ra 5 người để lập thành một tổ công tác sao cho phải có 1 tổ trưởng nam, 1 tổ phó nam và có ít nhất 1 nữ. Hỏi có bao nhiêu cách lập tổ công tác
Bài giải:
Chọn 3 tổ viên, trong đó có nữ.
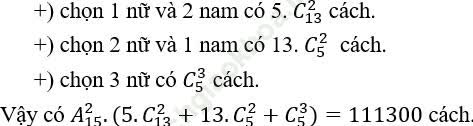
Bài 3: Một cuộc họp có 13 người, lúc ra về mỗi người đều bắt tay người khác một lần, riêng chủ tọa chỉ bắt tay ba người. Hỏi có bao nhiêu cái bắt tay?
Bài giải:
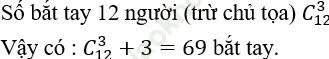
Bài 4: Một lớp có 33 học sinh, trong đó có 7 nữ. Cần chia lớp thành 3 tổ, tổ 1 có 10 học sinh, tổ 2 có 11 học sinh, tổ 3 có 12 học sinh sao cho trong mỗi tổ có ít nhất 2 học sinh nữ. Hỏi có bao nhiêu cách chia như vậy?
Bài giải:
TH1:

TH2:
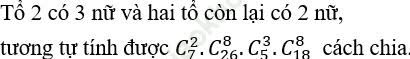
TH3:
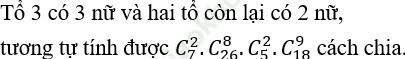
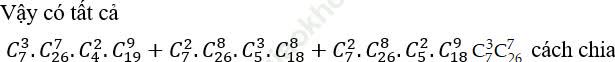
Bài 5: Từ 20 câu hỏi trắc nghiệm gồm 9 câu dễ, 7 câu trung bình và 4 câu khó người ta chọn ra 10 câu để làm đề kiểm tra sao cho phải có đủ cả 3 loại dễ, trung bình và khó. Hỏi có thể lập được bao nhiêu đề kiểm tra
Bài giải:
