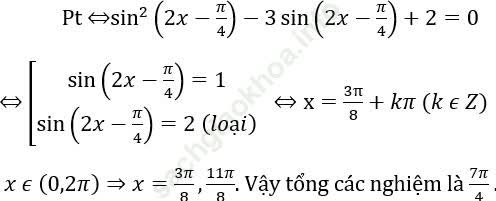Dạng 6: Cách giải các phương trình lượng giác đặc biệt - Chuyên đề Toán 11
A. Phương pháp giải & Ví dụ
Phương pháp giải
1. Sử dụng các công thức lượng giác và kết hợp với cách giải các phương trình lượng giác cơ bản.
2. Đánh giá, đặt ẩn phụ.
Ví dụ minh họa
Bài 1: Giải phương trình:
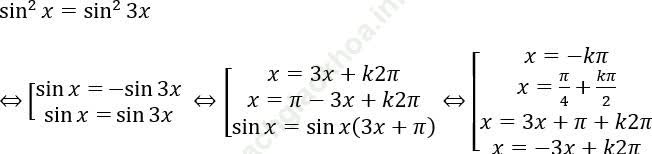

Bài 2: Giải phương trình: sin3xsin3x – cos3xcos3x = -2.5
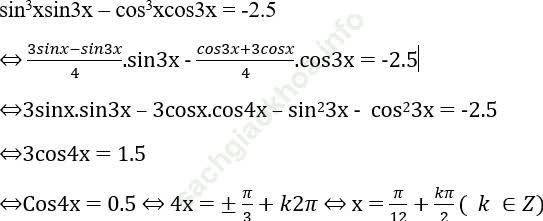
B. Bài tập vận dụng
Bài 1: Giải phương trình: sinx + sin2x + sin3x = cosx + cos2x +cos3x
Bài giải:
⇔ (sinx + sin3x) + sin2x = (cosx + cos3x) + cos2x
⇔ 2sin2xcosx + sin2x = 2cos2xcosx + cos2x.
⇔ sin2x (2cosx + 1) = cos2x (2cosx + 1)
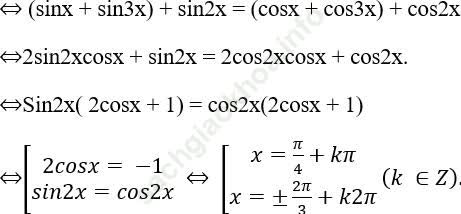
Bài 2: Giải phương trình: sinx + sin3x + sin5x = 0
Bài giải:
sinx + sin3x + sin5x = 0
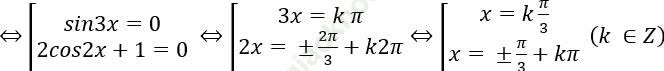
Bài 3: Giải phương trình: sin6x + cos6x = 0.25
Bài giải:
sin6x + cos6x = 0.25
⇔ (sin2x + cos2x)(cos4x + sin4x - sin2x cos2x) = 0.25
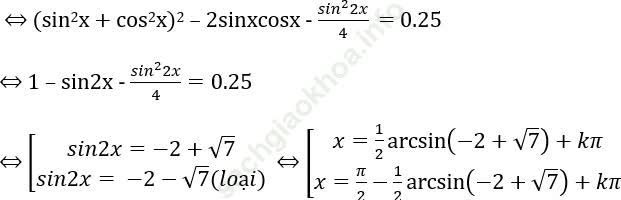
Bài 4: Tìm số nghiệm của phương trình: sin7x + cos22x = sin22x +sinx trong khoảng (0,5).
Bài giải:
sin7x + cos22x = sin22x+sinx

Bài 5: Tổng các nghiệm của phương trình:
sin2(2x - π /4) - 3cos (3 π /4 - 2x)+ 2 = 0 (1) trong khoảng (0; 2π)
Bài giải: