Cách chứng minh hai đường thẳng song song trong không gian - Chuyên đề Toán 11
A. Phương pháp giải
Để chứng ming hai đường thẳng song song trong không gian có thể sử dụng 1 trong 4 cách sau:
Cách 1: Chứng minh 2 đường thẳng đó đồng phẳng, rồi áp dụng phương pháp chứng minh song song trong hình học phẳng (như tính chất đường trung bình, định lí Talét đảo, …)
Cách 2: Chứng minh 2 đường thẳng đó cùng song song với đường thẳng thứ ba.
Cách 3: Nếu hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng song song thì giao tuyến của chúng (nếu có) cũng song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.
Cách 4: Áp dụng định lí về giao tuyến song song.
B. Ví dụ minh họa
Ví dụ 1: Cho tứ diện ABCD. Gọi I và J lần lượt là trọng tâm các tam giác ABC và ABD. Chọn mệnh đề đúng.
A. IJ // CD
B. IJ // AB
C. IJ và CD chéo nhau
D. IJ cắt AB
Bài giải:
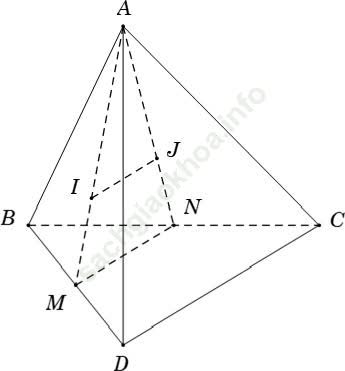
+ Gọi M và N lần lượt là trung điểm của BC và BD
⇒ MN là đường trung bình của tam giác BCD nên MN // CD (1)
+ Do I và J lần lượt là trọng tâm các tam giác ABC và ABD
⇒ AI/AM = AJ/AN = 2/3
⇒ IJ // MN (định lí Ta-let đảo) (2)
Từ (1) và (2) => IJ // CD
Mệnh đề đúng là: A
Ví dụ 2: Cho hình chóp S. ABCD có AD không song song với BC. Gọi M; N; P; Q; R; T lần lượt là trung điểm của AC; BD; BC; CD; SA và SD. Hai đường thẳng nào sau đây song song với nhau.
A. MP và RT
B. MQ và RT
C. MN và RT
D. PQ và RT
Bài giải:
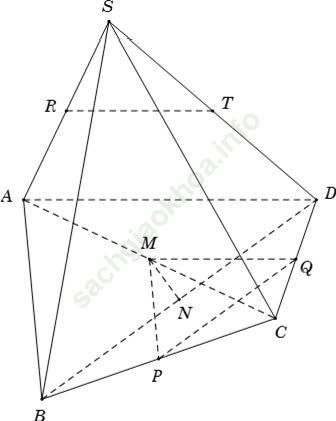
+ Ta có: M và Q lần lượt là trung điểm của AC; CD
⇒ MQ là đường trung bình của tam giác CAD nên MQ // AD (1)
+ Ta có: R và T lần lượt là trung điểm của SA; SD
⇒ RT là đường trung bình của tam giác SAD nên RT // AD (2)
+ Từ (1) và (2) suy ra: MQ // RT
Đáp án đúng là: B
Ví dụ 3: Cho hình chóp S. ABCD có đáy ABCD là hình bình hành. Gọi I; J; E và F lần lượt là trung điểm của SA; SB; SC và SD. Tìm đường thẳng không song song với IJ trong các đường thẳng sau:
A. EF
B. DC
C. AD
D. AB
Bài giải:
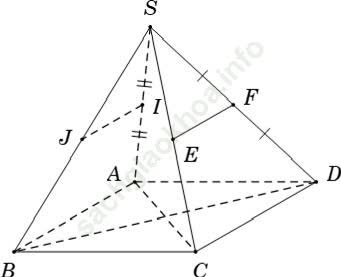
+ Xét tam giác SAB có IJ là đường trung bình
⇒ IJ // AB (tính chất đường trung bình trong tam giác) (1)
+ Xét tam giác SCD có EF là đường trung bình
⇒ EF // CD (2)
+ Mà ABCD là hình bình hành nên: AB// CD (3)
Từ (1); (2) và (3) => IJ // AB // CD // EF
Chọn đáp án: C
Ví dụ 4: Cho tứ diện ABCD. Gọi M; N là hai điểm phân biệt cùng thuộc đường thẳng AB. Hai điểm P và Q cùng thuộc đường thẳng CD. Xét vị trí tương đối của hai đường thẳng MP và NQ
A. MP // NQ
B. MP ≡ NQ
C. MP cắt NQ
D. MP và NQ chéo nhau
Bài giải:
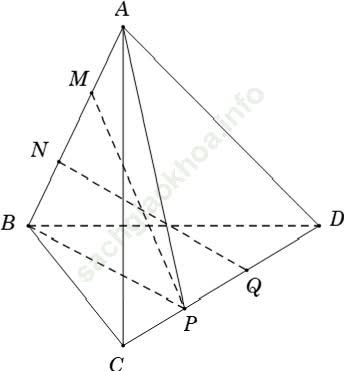
+ Xét mặt phẳng (ABP)
Ta có: M và N thuộc AB nên M và N thuộc mặt phẳng (ABP)
+ Mặt khác: CD ∩ (ABP) = P; và Q ∈ CD ⇒ Q không thuộc mặt phẳng (ABP).
⇒ 4 điểm M; N; P và Q không đồng phẳng.
Lưu ý 3 điểm A; M; N cùng thuộc mặt phẳng (ABP)
Chọn đáp án: D
Ví dụ 5: Cho hình chóp S. ABCD có đáy ABCD là hình bình hành. Gọi I; J lần lượt là trung điểm của các cạnh SA; SB. Tìm mệnh đề sai?
A. AB // IJ
B. CD // IJ
C. IJCD là hình thang
D. IJ và CD chéo nhau
Bài giải:
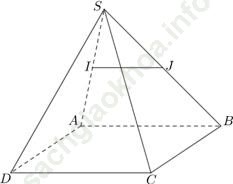
+ Vì I; J lần lượt là trung điểm của các cạnh SA; SB nên IJ là đường trung bình của tam giác SAB.
⇒ IJ // AB (1)
+ Lại có: AB // CD (2)
+ Từ (1) và (2) suy ra: IJ // CD
⇒ Tứ giác IJCD là hình thang.
Mệnh đề D là sai.
Ví dụ 6: Cho tứ diện ABCD. Gọi M; N lần lượt là các điểm thuộc các cạnh AB; AC sao cho: AM/AB = AN/AC; Gọi I và J lần lượt là trung điểm của BD; CD. Tìm mệnh đề sai?
A. MN // BC
B. IJ // BC
C. Điều kiện để tứ giác MNJI là hình bình hành là M; N là trung điểm của AB; AC
D. MN và IJ chéo nhau
Bài giải:
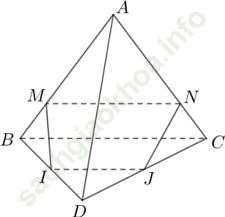
+ Ta có: AM/AB = AN/AC, từ đó => MN // BC (Định lý Ta-lét đảo)
+ Vì I và J lần lượt là trung điểm của BD và CD nên IJ là đường trung bình của tam giác BCD
⇒ IJ // BC (2)
+ Từ (1) và (2) suy ra MN // IJ. Vậy tứ giác MNJI là hình thang
+ Để MNJI là hình bình hành thì IJ = MN
Lại có: IJ = (1/2)BC (tính chất đường trung bình)
⇒ Để MNJI là hình bình hành thì MN = (1/2)BC
⇒ MN là đường trung bình của tam giác
⇒ M và N lần lượt là trung điểm của AB và AC
Mệnh đề sai là: D
Ví dụ 7: Cho hình chóp S. ABCD có đáy ABCD là hình bình hành và O là tâm của hình bình hành. Gọi M là trung điểm của SB. Qua M kẻ đường thẳng song song BC cắt SC tại N. Tìm mệnh đề sai.
A. MN // BC
B. MN // AD
C. NO // SA
D. NO // SD
Bài giải:
+ Xét mặt phẳng (SBC) có:
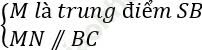
⇒ N là trung điểm của SC (định lí)
+ Ta có: M và N lần lượt là trung điểm của SB; SC nên MN là đường trung bình của tam giác SBC.
⇒ MN // BC // AD nên A và B đúng
+ Xét mặt phẳng (SAC) có N và O lần lượt là trung điểm của SC và AC nên NO là đường trung bình của tam giác SAC.
⇒ NO // SA nên C đúng
Vậy mệnh đề D sai.
Ví dụ 8: Cho hình chop S. ABCD có đáy ABCD là hình bình hành. Gọi N là điểm thuộc SB sao cho SN = (1/4)SB; gọi M là điểm trên cạnh SD sao cho SM = (1/3)MD. Tìm đường thẳng song song với BD?
A. MA
B. MN
C. NC
D. NS
Bài giải:
Trong mặt phẳng (SBD), ta có: SN = (1/4)SB nên SN/SB = 1/4
+ Do SM = (1/3)MD nên SM = (1/4)SD
⇒ SM/SD = SN/SB = 1/4
⇒ MN // BD (định lí ta-let đảo).
Chọn đáp án: B
C. Bài tập trắc nghiệm
Câu 1: Cho hình chóp S. ABCD đáy hình bình hành. Gọi A’; B’; C’; D’ lần lượt là trung điểm của các cạnh SA; SB; SC và SD. Trong các đường thẳng sau đây, đường thẳng nào không song song với A’B’?
A. AB
B. CD
C. C’D’
D. SC
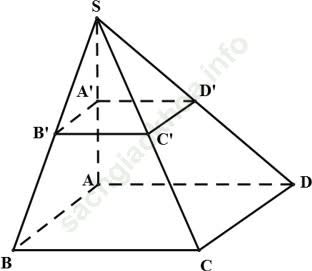
Chọn D
+ Do A’ và B’ là trung điểm của SA; SB
⇒ A’B’ là đường trung bình của tam giác SAB.
⇒ A’B’// AB (1).
+ Tương tự; C’D’ // CD (2)
+ Lại có: ABCD là hình bình hành nên AB // CD (3)
Từ (1); (2) và (3) suy ra: A’B’ // AB // CD // C’D’
⇒ D sai
Câu 2: Cho hình chóp S. ABCD có đáy ABCD là một hình thang với đáy lớn AB. Gọi M; N lần lượt là trung điểm của SA và SB. Gọi P là giao điểm của SC và (ADN), I là giao điểm của AN và DP. Khẳng định nào sau đây là đúng?
A. SI song song với CD
B. SI chéo với CD
C. SI cắt vớ CD
D. SI trùng với CD
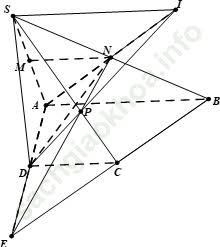
Chọn A
+ Trong (ABCD) gọi E = AD ∩ BC, trong (SCD) gọi P = SC ∩ EN
Ta có E ∈ AD ⊂ (ADN) ⇒ EN ⊂ (AND) ⇒ P ∈ (AND)
Vậy P = SC ∩ (ADN)
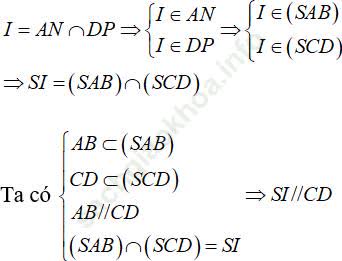
Câu 3: Cho hình chóp S. ABCD có đáy ABCD là một hình thang với đáy AD và BC. Biết AD = a và BC = b. Gọi I và J lần lượt là trọng tâm các tam giác SAD và SBC. Mặt phẳng (ADJ) cắt SB; SC lần lượt tại M; N. Mặt phẳng (BCI) cắt SA; SD tại P; Q. Khẳng định nào sau đây là đúng?
A. MN song song với PQ
B. MN chéo vớI PQ
C. MN cắt vớI PQ
D. MN trùng với PQ
Chọn A

Câu 4: Cho hình chóp S. ABCD có đáy ABCD là một hình thang với đáy AD và BC. Biết AD = a và BC = b. Gọi I và J lần lượt là trọng tâm các tam giác SAD và SBC. Mặt phẳng (ADJ) cắt SB; SC lần lượt tại M; N. Mặt phẳng (BCI) cắt SA; SD tại P; Q. Giả sử AM cắt BP tại E; CQ cắt DN tại F. Tính EF theo A; B.
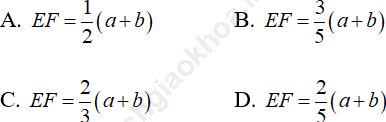
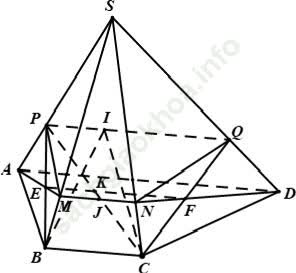
Chọn D
Trước tiên ta chứng minh EF song song với MN Và PQ
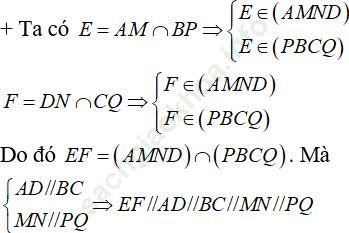

Câu 5: Cho tứ diện ABCD; M, N, P, Q lần lượt là trung điểm AC; BC; BD; AD. Tìm điều kiện để MNPQ là hình thoi.
A. AB = BC B. BC = AD C. AC = BD D. AB = CD
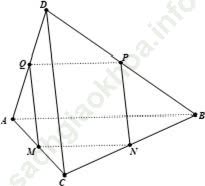
Chọn D
+ Ta có: M và N lần lượt là trung điểm của AC; CB
⇒ MN là đường trung bình của tam giác ACB
⇒ MN // AB
+ Tương tự; PQ // AB; MQ // CD và NP // CD
Suy ra: MN song song với PQ vì cùng song song với AB
MQ song song với PN vì cùng song song với CD
⇒ tứ giác MNPQ là hình bình hành.
+ Tứ giác MNPQ là hình thoi khi: MQ = PQ ⇔ AB = CD
Câu 6: Cho hình chóp A. BCD; gọi M, N lần lượt là trung điểm của BD, BC. Gọi G1, G2 lần lượt là trọng tâm tam giác ABD và ABC. Tìm mệnh đề đúng?
A. MN và G1G2 chéo nhau
B. G1G2 // MN
C. MN cắt G1G2
D. G2M và G1N chéo nhau
+ Xét tam giác AMN ta có:
⇒ MN // G1G2
Do đó; 2 đường thẳng MN và G1G2 đồng phẳng và 2 đường thẳng G2M, G1N sẽ cắt nhau.
Chọn B
Câu 7: Cho hình chóp S. ABCD đáy là tứ giác lồi. Gọi M là giao điểm của AC và BD. Gọi G1; G2 lần lượt là trọng tâm tam giác SOD và SOB. Tìm đường thẳng song song với G1G2?
A. SH B. Sk C. HK D. KC
+ Gọi H là trung điểm của OD và K là trung điểm của OB.
+ Do G1 là trọng tâm tam giác SOD nên: (SG1)/SH = 2/3
+ DO G2 là trọng tâm tam giác SOB nên: (SG2)/SK = 2/3
+ Trong mp (SG1G2) ta có: (SG1)/SH = (SG2)/SK = 2/3
⇒ G1G2 // HK (định lí Ta- let)
Chọn C
Câu 8: Cho tứ diện ABCD có M; N lần lượt thuộc AB; DB sao cho MN // AD. Gọi I là trung điểm BC. Gọi HK là giao tuyến của mp (CNM) và mp (AID). Tìm mệnh đề đúng?
A. HK // AD
B. HK // MI
C. K là trọng tâm tam giác ABC
D. Tất cả sai
+ Xét hai mp (CNM) và mp (AID) có:
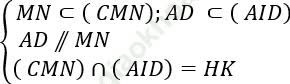
⇒ HK // AD // MN (hệ quả)
+ Do M là điểm bất kì trên cạnh AB nên chưa chắc K là trọng tâm tam giác ABC
⇒ A đúng
Chọn A