Tìm nghiệm của phương trình lượng giác cơ bản trên khoảng (đoạn) - Chuyên đề Toán 11

A. Phương pháp giải

+ Để giải phương trình trên khoảng (a; b) (hoặc trên đoạn) thì ta cần:

• Bước 1: Tìm họ nghiệm của phương trình đã cho.

• Bước 2: Giải bất phương trình:

⇒ Các giá trị nguyên của k=... ⇒ Các nghiệm của phương trình trong khoảng (đoạn) đã cho.

+ Để giải bất phương trình có chứa điều kiện ta cần:

• Bươc 1: Tìm điều kiện xác định của phương trình (nếu có).

• Bước 2: Biến đổi phương trình đưa về phương trình lượng giác cơ bản

• Bước 3: Giải phương trình lượng giác cơ bản

• Bước 4: Kết hợp với điều kiện xác định ⇒ nghiệm của phương trình.

B. Ví dụ minh họa

Ví dụ 1. Số nghiệm của phương trình tanx= tan3π/11 trên khoảng (π/4; 2π) là?

A. 1

B. 2

C. 3

D. 4

Bài giải:

Đáp án đúng là: B.

Hướng dẫn:

Ta có tanx = tan (3π/11)

⇔ x = 3π/11 + kπ k∈Z

Do x∈ (π/4; 2π) nên π/4 < 3π/11 + kπ < 2π

⇔ 1/4 < 3/11 + k < 2

⇔ (- 1)/44 < k < 19/11

Mà k nguyên nên k ∈ {0; 1}

Tương ứng với hai giá trị của k cho ta hai nghiệm của phương trình đã cho thỏa mãn điều kiện đề bài.

Ví dụ 2. Số nghiệm của phương trình: sin (x- π/4)= (- 1)/√ 2 với là:

A. 1

B. 2

C. 3

D. 4

Bài giải:

Đáp án đúng là: D

Hướng dẫn:

Ta có: sin (x - π/4) = (- 1)/√ 2

⇒ sin (x - π/4) = sin⁡ (- π/4)

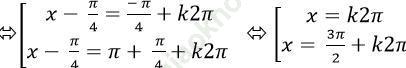
+ Xét họ nghiệm x = k2π với π ≤ x ≤ 5π

⇒ π ≤ k2π ≤ 5π

⇒ 1/2 ≤ x ≤ 5/2

Mà k nguyên nên k = 1 hoặc k = 2

⇒ Họ nghiệm này cho ta 2 nghiệm thỏa mãn điều kiện.

+ Xét họ nghiệm x = 3π/2 + k2π với π ≤ x ≤ 5π

⇒ π ≤ 3π/2 + k2π ≤ 5π

⇒ 1/2 ≤ x ≤ 5/2

Vì k nguyên nên k∈ {0; 1}.

⇒ Họ nghiệm này cho ta 2 nghiệm của x thỏa mãn điều kiện.

Vậy phương trình đã cho có bốn nghiệm thỏa mãn điều kiện => Chọn D

Ví dụ 3. Số nghiệm của phương trình: cos⁡ (x + π/3) = √ 2/2 với 0 ≤ x ≤ 2π là:

A. 0.

B. 2.

C. 1.

D. 3.

Bài giải:

Đáp án đúng là: D

Hướng dẫn:

Ta có: cos⁡ (x + π/3) = √ 2/2

⇒ cos⁡ (x + π/3) = cos π/4

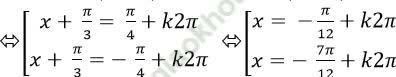
+ Xét họ nghiệm: x = -π/12 + k2π

Để 0 ≤ x ≤ 2π thì 0 ≤ -π/12 + k2π ≤ 2π

⇔ π/12 ≤ k2π ≤ 25π/12

⇔ 1/24 ≤ k ≤ 25/24

Mà k nguyên nên k = 1 khi đó x = 23π/12

+ Xét họ nghiệm x = -7π/12 + k2π

Để 0 ≤ x ≤ 2π thì 0 ≤ -7π/12 + k2π ≤ 2π

⇔ 7π/12 ≤ k2π ≤ 31π/12

⇔ 7/24 ≤ k ≤ 31/24

Mà k nguyên nên k = 1 khi đó x = 17π/12

Vậy phương trình có hai nghiệm 0 ≤ x ≤ 2π là: x = 23π/12 và x = 17π/12

Ví dụ 4. Tìm nghiệm của phương trình: tanx = 1 trên đoạn (0; 180⁰)

A. 45⁰; 135⁰

B. 135⁰

C. 45⁰

D. Đáp án khác

Bài giải:

Đáp án đúng là: C

Hướng dẫn:

Ta có; tanx = 1 ⇔ tanx = 45⁰

⇔ x= 45⁰+ k. 180⁰ với k∈ Z.

+Để 0⁰ < x < 180⁰ thì 0⁰ < 45⁰+ k. 180⁰ < 180⁰

⇔ - 45⁰ < k. 180⁰ < 135⁰

⇔ (- 45)/180 < k < 135/180

Mà k nguyên nên k = 1. Khi đó; x = 45⁰

Vậy phương trình tanx = 1 có một nghiệm thuộc khoảng (0⁰; 180⁰)

Ví dụ 5. Tìm tổng các nghiệm của phương trình cosx = sinx trên đoạn [0; π]

A. 3π/4

B. π/2

C. π/4

D. Đáp án khác

Bài giải:

Đáp án đúng là: C.

Hướng dẫn:

Ta có: cosx = sinx ⇒ cos x = cos (π/2-x)

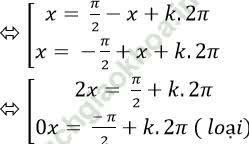
⇔ x = π/4 + kπ

Xét các nghiệm trên đoạn [0; π] ta có:

0 < π/4 + kπ < π

⇔ - π/4 < kπ < 3π/4

⇔ (- 1)/4 < k < 3/4

Mà k nguyên nên k= 0. Khi đó; x = π/4 => Chọn C

Ví dụ 6. Cho phương trình sin (x + π/6) = 1/2. Tìm tổng các nghiệm của phương trình trên đoạn [0; π]

A. π/6

B. π/3

C. x= 4π/3

D. x= 2π/3

Bài giải:

Đáp án đúng là: D.

Hướng dẫn:

Ta có: sin (x + π/6) = 1/2

⇒ sin (x + π/6) = sin π/6

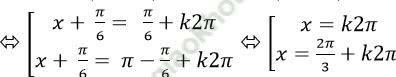
+ Xét họ nghiệm x = k2π. Ta có:

0 ≤ k2π ≤ π

⇒ 0 ≤ k ≤ 1/2

Mà k nguyên nên k = 0. Khi đó, nghiệm của phương trình là x= 0

+ Xét họ nghiệm x = 2π/3 + k2π. Ta có: 0 ≤ 2π/3+ k2π ≤ π ⇔ (- 2)/3 ≤ k ≤ 1/6

Mà k nguyên nên k = 0. Khi đó, x = 2π/3

Vậy trên đoạn [0; π] phương trình đã cho có 2 nghiệm là x = 0 và x = 2π/3

⇒ Tổng hai nghiệm là 2π/3

Ví dụ 7. Cho phương trình tan (x + 45⁰) = √ 3. Tìm các nghiệm của phương trình trên khoảng (90⁰; 360⁰)

A. 175⁰

B. 195⁰

C. 215⁰

D. Đáp án khác

Bài giải:

Đáp án đúng là: B.

Hướng dẫn:

Ta có: tan (x + 45⁰) = √ 3

⇔ tan (x + 45⁰) = tan 60⁰

⇔ x + 45⁰ = 60⁰ + k. 180⁰

⇔ x= 15⁰ +k. 180⁰

Các nghiệm của phương trình trên khoảng (90⁰; 360⁰) thỏa mãn:

90⁰ < 15⁰ + k. 180⁰ < 360⁰

< 75⁰ < k. 180⁰ < 345⁰

< 75/180 < k < 345/180

Mà k nguyên nên k= 1

Với k = 1 ta có x= 195⁰

Ví dụ 8. Cho phương trình sinx = 0. Biết số nghiệm của phương trình trên khoảng (0⁰; a⁰) là 3. Tìm điều kiện của a.

A. a > 540

B. a > 360

C. a > 270

D. a > 630

Bài giải:

Ta có: sinx = 0 ⇒ x = k. 180⁰ với k nguyên

Ta xét số nghiệm cua phương trình trên khoảng (0⁰; a⁰)

0⁰ < k. 180⁰ < a⁰

⇒ 0 < k < a/180 (1)

Do phương trình đã cho có đúng 3 nghiệm trên khoảng (0⁰;a⁰) nên k∈ {1; 2; 3} (2)

Từ (1) và (2) suy ra: a/180 > 3 ⇔ a > 540

Vậy điều kiện của a là a > 540.

Đáp án đúng là: A.

Ví dụ 9. Cho phương trình tan (x + π/3) = √ 3. Tìm số nghiệm của phương trình đã cho trên khoảng (0; 6π).

A. 3

B. 4

C. 5

D. 6

Bài giải:

Đáp án đúng là: C.

Hướng dẫn:

Ta có: tan (x + π/3) = √ 3

⇔ tan (x + π/3) = tan π/3

⇒ x + π/3 = π/3 + kπ

⇒ x = kπ với k nguyên

Xét các nghiệm của phương trình trên khoảng (0; 6π) thỏa mãn:

0 < kπ < 6π

⇒ 0 < k < 6

Do k nguyên nên k∈ {1; 2; 3; 4; 5}

Vậy số nghiệm của phương trình đã cho trên (0; 6π) là 5.

Ví dụ 10. Cho phương trình cos (x + 30⁰) = cos (x + 90⁰). Tính số nghiệm của phương trình trên đoạn [180⁰; 630⁰]

A. 3

B. 2

C. 4

D. 5

Bài giải:

Đáp án đúng là: A.

Hướng dẫn:

Ta có: cos (x+ 30⁰) = cos (x+ 90⁰)

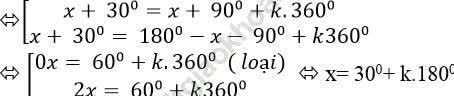
Các nghiệm của phương trình trên đoạn [180⁰; 630⁰] thỏa mãn:

⇔ 180⁰ ≤ 30⁰ + k180⁰ ≤ 630⁰

⇔ 150⁰ ≤ k180⁰ ≤ 600⁰

⇔ 5/6 ≤ k ≤ 10/3

Mà k nguyên nên k∈ {1; 2; 3}

Vậy số nghiệm của phương trình đã cho trên [180⁰; 630⁰] là 3

Ví dụ 11. Cho phương trình cot (x - 30⁰) = tanx. Tìm số nghiệm của phương trình đã cho trên khoảng (- 270⁰; 0⁰)

A. 4

B. 3

C. 5

D. 2

Bài giải:

Đáp án đúng là: D.

Hướng dẫn:

Ta có: cot (x - 30⁰) = tanx

⇔ cot (x - 30⁰) = cot (90⁰- x)

⇔ x - 30⁰ = 90⁰ – x + k. 180⁰

⇔ 2x = 120⁰ + k. 180⁰ ⇔ x = 60⁰ + k. 180⁰

Các nghiệm của phương trình đã cho trên khoảng (-270⁰; 0⁰) thỏa mãn:

- 270⁰ < 60⁰ + k. 180⁰ < 0⁰

⇔ -330⁰ < k. 180⁰ < - 60⁰

⇔ (- 33)/18 < k < (-1)/3

Mà k nguyên nên k∈ {-2; -1}

Vậy có hai nghiệm của phương trình đã cho trên khoảng (-270⁰; 0⁰)

Ví dụ 12. Cho phương trình: √ 3cos⁡x + m - 1 = 0. Với giá trị nào của m thì phương trình có nghiệm:

A. m < 1 - √ 3.

B. m > 1 + √ 3.

C. 1 - √ 3 ≤ m ≤ 1 + √ 3.

D. -√ 3 ≤ m ≤ √ 3.

Bài giải:

Đáp án đúng là: C.

Hướng dẫn:

Ta có: 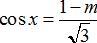có nghiệm khi và chỉ khi:

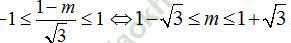
C. Bài tập vận dụng

Câu 1: Cho phương trình √ 6 sinx - (3√ 2)/2 = 0. Tìm số nghiệm của phương trình trên khoảng (0; 4π)?

A. 4

B. 5

C. 6

D. 7

Hiển thị lời giải

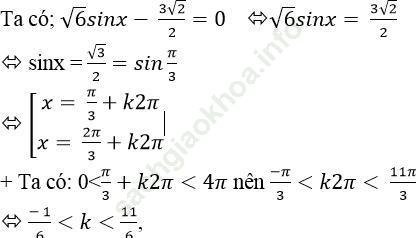
mà k nguyên nên k =0 hoặc 1.

+ Tương tự; có 0 < 2π/3+k2π < 4π nên (-2π)/3 < k2π < 10π/3

⇒ (- 2)/6 < k < 10/6, mà k nguyên nên k =0 hoặc 1.

⇒ Phương trình đã cho có tất cả bốn nghiệm trên khoảng (0; 4π)

Chọn A.

Câu 2:Cho phương trình sin (x+ 10⁰) = cos (x- 20⁰). Tìm số nghiêm của phương trình trên khoảng (90⁰; 360⁰)?

A. 0

B. 1

C. 2

D. 4

Hiển thị lời giải

Ta có: sin (x+10⁰) = cos (x-20⁰)

⇔ sin (x+10⁰) = sin (90⁰- x+ 20⁰)

⇔ sin (x+10⁰) = sin (110⁰- x)

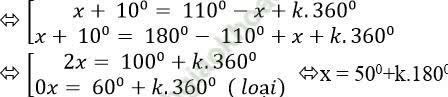
Ta có: 90⁰ < 50⁰+ k. 180⁰ < 360⁰

⇔ 40⁰ < k. 180⁰ < 310⁰ ⇒ 4/18 < k < 31/18

Mà k nguyên nên k= 1.

⇒ Trên khoảng (90⁰;360⁰) phương trình đã cho có đúng một nghiệm.

Chọn B.

Câu 3:Tìm số nghiệm của phương trình sinx= cos (2x- 30⁰) trên khoảng (60⁰; 360⁰)

A. 0

B. 2

C. 3

D. 1

Hiển thị lời giải

Lời giải

Ta có: sinx= cos (2x- 30⁰)

⇔ cos (90⁰- x) =cos (2x- 30⁰)

+ khi đó: 60⁰ < 40⁰ – k. 360⁰ < 360⁰

⇔ 20⁰ < - k. 360⁰ < 320⁰

⇔ (-32)/36 < k < (- 1)/18

Mà k nguyên nên không có giá trị nguyên nào của k thỏa mãn.

+ Tương tự; 60⁰ < -60⁰ + k. 360⁰ < 360⁰

⇔ 120⁰ < k. 360⁰ < 420⁰

⇔ 1/3 < k < 7/6

Mà k nguyên nên k= 1.

⇒ Phương trình đã cho có đúng một nghiệm thuộc khoảng (60⁰;360⁰)

Chọn D.

Câu 4: Cho phương trình: √ 6 cot⁡ (π/2-x)+ √ 2=0. Tìm số nghiệm của phương trình trên khoảng (π; 4π)?

A. 2

B. 3

C. 4

D. 5

Hiển thị lời giải

Ta có: √ 6 cot⁡ (π/2-x)+ √ 2=0

⇔ √ 6. tanx+ √ 2=0

⇔ tanx= (- 1)/√ 3 = tan (-π)/6

⇔ x= (-π)/6+kπ

+ khi đó; π < (-π)/6+kπ < 4π

⇔ 7π/6 < kπ < 25π/6 ⇔ 7/6 < k < 25/6

Mà k nguyên nên k∈ {2; 3; 4}.

⇒ phương trình đã cho có 3 nghiệm thuộc khoảng (π; 4π).

Chọn B.

Câu 5:Phương trình cosx= m+ 1 có nghiệm khi m là

A. -1≤ m≤ 1.

B. m≤ 0.

C. m≥ -2.

D. -2≤ m≤ 0.

Hiển thị lời giải

Chọn D.

Áp dụng điều kiện nghiệm của phương trình cosx=a

+ Phương trình có nghiệm khi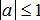

+ Phương trình có nghiệm khi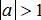

Ta có phương trình cosx = m+ 1 có nghiệm khi và chỉ khi:

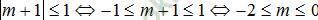
Câu 6: Nghiệm âm lớn nhất và nghiệm dương nhỏ của phương trình sin4x + cos5x=0 theo thứ tự là:

A.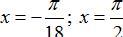

B.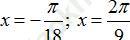

C.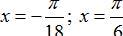

D.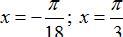

Hiển thị lời giải

Chọn C.

sin4x + cos5x=0 ⇒ cos5x=-sin4x

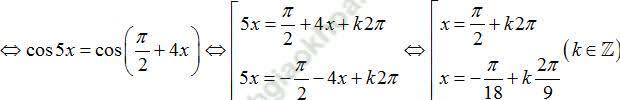
Với nghiệm x=π/2+k2π ta có nghiệm âm lớn nhất và nhỏ nhất là -3π/2 và π/2

Với nghiệm x=-π/18 + k2π/9 ta có nghiệm âm lớn nhất và nhỏ nhất là -π/18 và π/6

Vậy hai nghiệm theo yêu cầu đề bài là -π/18 và π/6

Câu 7:Tìm tổng các nghiệm của phương trình trên

A. 7π/18

B. 4π/18

C. 47π/8

D. 47π/18

Hiển thị lời giải

Ta có: sin (5x+ π/3)=cos⁡ (2x- π/3)

Suy ra các nghiệm: x=11π/18

Vậy tổng các nghiệm là: 47π/18.

Chọn D.

Câu 8:Trong nửa khoảng, phương trình cos2x+ sinx=0 có tập nghiệm là

A.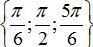

B.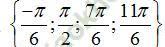

C.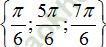

D.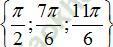

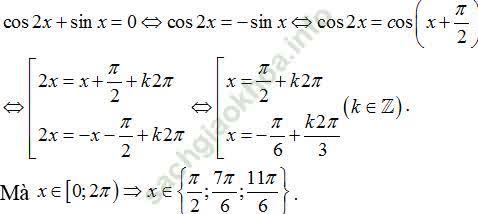
Hiển thị lời giải

Chọn D.

Câu 9:Cho phương trình sinx + √ 3. sin π/6=0. Tìm số nghiệm của phương trình trên khoảng (4π; 10π)?

A. 5

B. 6

C. 7

D. 4 Lời giải

Hiển thị lời giải

Ta có: sinx + √ 3. sin π/6=0 ⇒ sinx + √ 3.1/2=0

⇔ sin x= (- √ 3)/2=sin (-π)/3

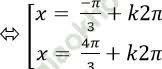
+ Ta có: 4π < (-π)/3+k2π < 10π

⇔ 13π/3 < k2π < 31π/3 ⇔ 13/6 < k < 31/6

Mà k nguyên nên k∈ {3; 4; 5}

+ Tương tự; ta có: 4π < 4π/3+k2π < 10π

⇔ 8π/3 < k2π < 26π/3 ⇔ 4/3 < k < 13/3

Mà k nguyên nên k∈ {2; 3; 4}

Kết hợp cả hai trường hợp; suy ra phương trình đã cho có tất cả 6 nghiệm trên khoảng (4π; 10π).

Chọn B.

Bài trước: Giải phương trình lượng giác cơ bản - Chuyên đề Toán 11 Bài tiếp: Phương trình quy về phương trình lượng giác cơ bản - Chuyên đề Toán 11