Dạng 1: Tìm vi phân của hàm số - Chuyên đề Toán 11
A. Phương pháp giải & Ví dụ
Cho hàm có y = f (x) xác định trên (a; b) và có đạo hàm tại x ∈ (a; b). Giả sử Δ x là số gia của x sao cho x + Δ x ∈ (a; b)
Tích f ' (x)Δ x (hay y 'Δ x) được gọi là vi phân của hàm số f (x) tại x, ứng với số gia Δ x, kí hiệu là df (x) hay dy
Lưu ý: Vì dx = Δ x nên: dy = df (x) = f ' (x)dx
Ứng dụng vi phân vào phép tính gần đúng
Với |Δ x| đủ nhỏ, ta có: 
hay Δ y = f (x0 + Δ x) - f (x0) = f ' (x0)Δ x
=> f (x0 + Δ x) ≈ f (x0) + f ' (x0)Δ x ≈ f (x0) + df (x0)
Ví dụ minh họa
Bài 1: Cho hàm số y = sinx – 3cosx. Tính vi phân của hàm số.
Bài giải:
Ta có: dy = (sinx – 3cosx)’dx = (cosx + 3sinx)dx
Bài 2: Cho hàm số: 
. Tính vi phân của hàm số đó.
Bài giải:
Ta có:
Bài 3: Xét hàm số y = 
Tính vi phân của hàm số đó.
Bài giải:
Ta có:
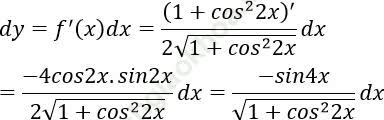
Bài 4: Cho hàm số y = x3 - 5x + 6. Tính vi phân của hàm số đó.
Bài giải:
Ta có: dy = (x3-5x+6)'dx = (3x2-5)dx
Bài 5: Cho hàm số y = 1/ (3x3). Tính vi phân của hàm số đó
Bài giải:
Ta có: 
Bài 6: Cho hàm số 
.Tính vi phân của hàm số đó.
Bài giải:
Ta có: 
Bài 7: Cho hàm số: 
. Tính vi phân của hàm số đó
Bài giải:
Ta có:
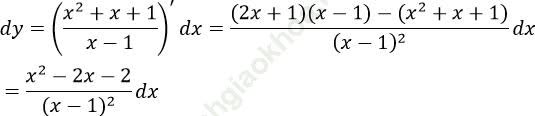
B. Bài tập vận dụng
Bài 1: Tìm vi phân của hàm số y = xsinx + cosx.
A. dy = xcosxdx
B. dy = xcosx
C. dy = (2sinx + xcosx)dx
D. dy = (sinx+cosx)dx
Đáp án: A
Ta có:
y’ = sinx + xcosx – sinx = xcosx
=> dy = xcosxdx
Bài 2: Tìm vi phân của hàm số: 
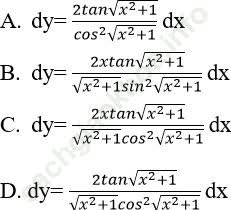
Đáp án: C
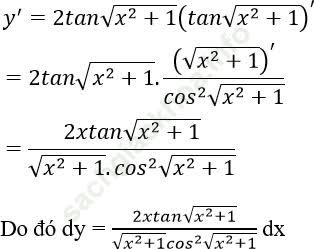
Chọn đáp án C
Bài 3: Cho hàm số f (x) = x2 - x + 2. Tính Δ f (1) và df (1)nếu Δ x = 0,1
A. Δ f (1) = 0,11; df (1) = 0,2
B. Δ f (1) = 0,11; df (1) = 0,1
C. Δ f (1) = 0,2; df (1) = 0,11
D. Δ f (1) = 0,2; df (1) = 0,1
Đáp án: B
Ta có: Δ f (1) = f (1+ 0.1) - f (1) = 0.11 và df (1) = f ' (1).Δ x = 0.1
Đáp án B
Bài 4: Tìm vi phân của hàm số y = (2x+1)5
A. dy = 10 (2x+1)4
B. dy = 5 (2x+1)4 dx
C. dy = (2x+1)4 dx
D. dy = 10 (2x+1)4 dx
Đáp án: A
Ta có: dy = f ' (x)dx = 5 (2x+1)4.2dx = 10 (2x+1)4dx
Đáp án A
Bài 5: Tìm vi phân của hàm số y = cos3(1-x)
A. dy = -sin2(1-x)dx
B. dy = 3cos2(1-x).sin (1-x)dx
C. dy = -3cos2(1-x)sin (1-x)dx
D. dy = 3cos2(1-x)dx
Đáp án: A
Ta có: dy = f ' (x)dx = 3cos2 (1-x)(cos (1-x))' dx
= -3cos2 (1-x)sin (1-x) (1-x)' dx
= 3cos2 (1-x)sin (1-x)dx
Đáp án A
Bài 6: Tìm vi phân của hàm số: 
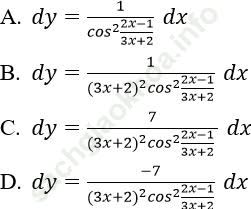
Đáp án: C
Ta có:
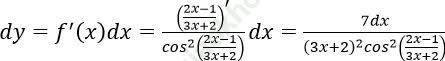
Bài 7: Tính vi phân của hàm số y = sin3(2x+1)
A. dy = 3sin2(2x+1)cos (2x+1)dx
B. dy = -6sin2(2x+1)cos (2x+1)dx
C. dy = 6sin2(2x+1)cos (2x+1)dx
D. dy = 3sin2(2x+1)cos (2x+1)dx
Đáp án: C
Đáp án C
Ta có: dy = f ' (x)dx = 6sin2(2x+1)cos (2x+1)dx
Bài 8: Cho hàm số y = f (x) = (x-1)2. Biểu thức nào sau đây chỉ vi phân của hàm số f (x)?
A. dy = 2 (x – 1)dx
B. dy = (x-1)2 dx
C. dy = 2 (x – 1)
D. dy = (2x – 1)dx
Đáp án: A
Chọn A.
Ta có dy = f ' (x)dx = 2 (x-1)dx
Bài 9: Tìm vi phân của các hàm số: y = x3 + 2x2
A. dy = (3x2-4x)dx
B. dy = (3x2+x)dx
C. dy = (3x2+2x)dx
D. dy = (3x2+4x)dx
Đáp án: D
Chọn D
dy = (3x2 + 4x)dx
Bài 10: Tìm vi phân của các hàm số: 
Đáp án: D
Chọn D
Bài 11: Cho hàm số y = x3 - 9x2 + 12x - 5. Vi phân của hàm số là:
A. dy = (3x2-18x+12)dx
B. dy = (-3x2-18x+12)dx
C. dy = - (3x2-18x+12)dx
D. dy = (-3x2+18x-12)dx
Đáp án: A
Chọn A
Ta có
dy = (x3-9x2+12x-5)'dx = (3x2-18x+12)dx
Bài 12: Tìm vi phân của các hàm số y = (3x+1)10
A. dy = 10 (3x+1)9 dx
B. dy = 30 (3x+1)10 dx
C. dy = 9 (3x+1)10 dx
D. dy = 30 (3x+1)9 dx
Đáp án: D
Chọn D
dy = 30 (3x+1)9dx
Bài 13: Tìm vi phân của các hàm số y = sin2x + sin3x
A. dy = (cos2x + 3 sin2x cosx)dx
B. dy = (2cos2x + 3 sin2x cosx)dx
C. dy = (2cos2x + sin2x cosx)dx
D. dy = (cos2x + sin2x cosx)dx
Đáp án: B
Chọn B
dy = (2cos2x+ 3sin2xcosx)dx
Bài 14: Tìm vi phân của các hàm số y = tan2x.
A. dy = (1 + tan22x)dx
B. dy = (1 - tan22x)dx
C. dy = 2 (1 - tan22x)dx
D. dy = 2 (1 + tan22x)dx
Đáp án: D
Chọn D
dy = 2 (1+tan22x)dx
Bài 15: Tìm vi phân của các hàm số
Đáp án: D
Chọn D
