Cách tính tổng n số hạng đầu tiên của cấp số cộng cực hay có lời giải - Chuyên đề Toán 11
A. Phương pháp giải
Cho cấp số cộng (un) có số hạng đầu là u1; công sai là d. Tổng n số hạng đầu tiên của cấp số cộng là:
+ Ngoài ra, ta có 1 cách tính khác đó là: ![]()
+ Lưu ý: Cho dãy số (un) là cấp số cộng có công sai d. Cho x và y là hai số hạng của cấp số cộng. Khi đó từ x đến y có số số hạng là: ![]()
B. Ví dụ minh họa
Ví dụ 1: Cho cấp số cộng (un) có u5 = − 10 và u15 = 60. Tổng của 20 số hạng đầu tiên của cấp số cộng là:
A. S20 = 560
B. S20 = 480
C. S20 = 570
D. S20 = 475
Bài giải:
Ta có: 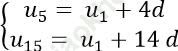
Theo giả thiết ta có: 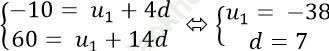
Tổng 20 số hạng đầu tiên của cấp số cộng là:
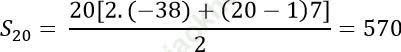
Đáp án đúng là: C.
Ví dụ 2: Cho cấp số cộng (un) thỏa mãn: ![]() . Tính tổng
S = u5 + u6 +.. + u30
. Tính tổng
S = u5 + u6 +.. + u30
A. – 1243
B. -1235
C. – 1345
D. - 1450
Bài giải:
* Từ giả thiết bài toán, ta có:
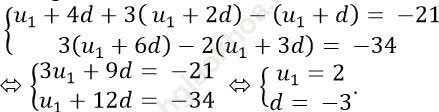
* Ta có: u5; u6;... ; u30 là cấp số cộng có 26 số hạng;
+) Số hạng đầu: u5 = 2 + 4. (-3) = -10; công sai d = -3
=> Tổng ![]()
Đáp án đúng là: B.
Ví dụ 3: Cho dãy số (un) có d = –2; S8 = 72. Tính u1?
A. u1 = 16
B. u1 =- 16
C. u1 = 8
D. u1 = - 4
Bài giải:
* Ta có: ![]()
* Lại có: u8 = u1 + 7d => u8 – u1 = 7d = -14 (2)
Từ (1) và (2) ta có hệ phương trình:
Đáp án đúng là: A.
Ví dụ 4: Cho dãy số (un) là một cấp số cộng có u1 = -1; d = 2 và Sn= 483. Tính số các số hạng của cấp số cộng?
A. n = 20
B. n= 21
C. n= 22
D. n= 23.
Bài giải:
Tổng của n số hạng đầu tiên của cấp số cộng là:
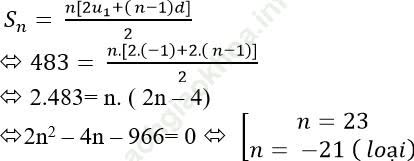
Đáp án đúng là: D.
Ví dụ 5: Cho (un) là cấp số cộng thỏa mãn: 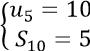 . Tính tổng của số hạng đầu và công sai của cấp số cộng.
. Tính tổng của số hạng đầu và công sai của cấp số cộng.
A. 63
B. 67
C. 75
D. 81
Bài giải:
Theo giả thiết ta có:
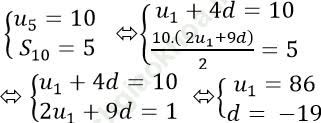
=> Tổng của số hạng đầu và công sai của cấp số cộng là: 86 + (− 19) = 67
Đáp án đúng là: B.
Ví dụ 6: Cho một cấp số cộng (un) có u1 = 1 và tổng 100 số hạng đầu bằng 24850. Tính
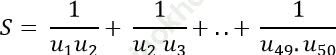

Hướng dẫn giải:
Gọi d là công sai của cấp số đã cho.
Ta có:
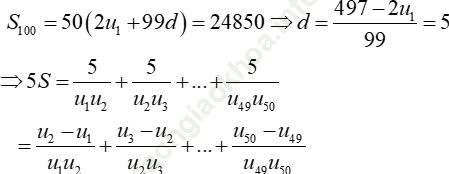
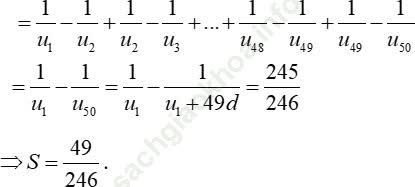
Đáp án đúng là: D.
Ví dụ 7: Cho cấp số cộng (un) thỏa mãn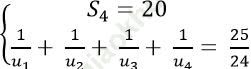 . Tìm số hạng đầu tiên của cấp số cộng.
. Tìm số hạng đầu tiên của cấp số cộng.
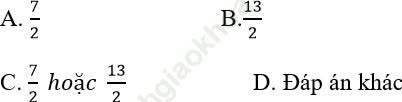
Bài giải:
Theo giả thiết ta có:
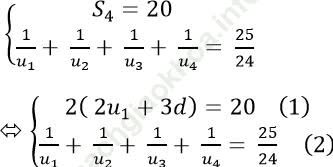
Từ (1) suy ra:
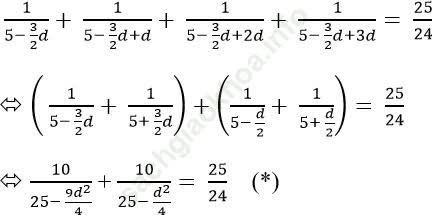
Đặt: ![]() khi đó phương trình (*) trở thành:
khi đó phương trình (*) trở thành:
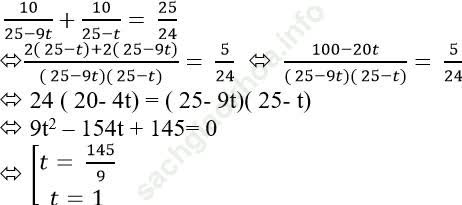
* Với ![]() thì
thì ![]()
Với ![]()
Với ![]()
* Với t = 1 => d2 = 1 ⇔ d= ± 1
Với ![]()
Với ![]()
Vậy ứng với 4 trường hơp sẽ có 4 giá trị của u1 thỏa mãn.
Đáp án đúng là: D.
Ví dụ 8: Cho cấp số cộng (un) thỏa mãn: u4 + u8 + u11 + u17 = 100. Tính S19
A. 475
B. 500
C. 1000
D. 750
Bài giải:
* Theo giả thiết ta có:
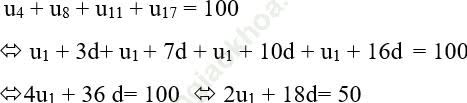
* Do đó: ![]()
Đáp án đúng là: A.
Ví dụ 9: Cho (un) là cấp số cộng thỏa mãn: u2 + u3 + u7 + u10 + u12 + u17 = 300.
Tính u9 + u8
A. 50
B. 150
C. 75
D. 100
Bài giải:
*Theo giả thiết ta có:
u2 + u3 + u7 + u10 + u12 + u17 = 300
⇔ u1 + d + u1 + 2d + u1 + 6d + u1 + 9d + u1 +11d+ u1 + 16d = 300
⇔ 6u1 + 45d = 300 ⇔ 2u1 + 15d = 100
* Do đó: ![]()
Đáp án đúng là: D.
Ví dụ 10: Cho (un) là cấp số cộng và Sm = Sn với m ≠ n. Tính Sm+n
A. 0
B. Sm − Sn
C. Sn − Sm
D. Sn + Sm
Bài giải:
* Ta có:
Do Sm = Sn với m ≠ n nên ta có:
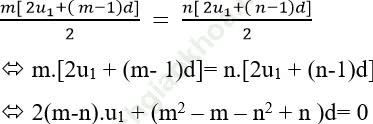
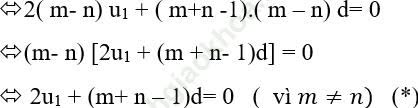
* Ta có:
Đáp án đúng là: A.
Ví dụ 11: Tính tổng sau: S = 2 + 4 + 6 +... + (2n − 2) + 2n
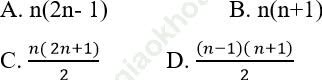
Bài giải:
Ta có dãy số 2,4,6,.. , 2n − 2,2n là cấp số cộng với công sai d = 2 và u1 = 2, số hạng tổng quát un= 2 + 2 (n-1) = 2n. Dãy số này có n số hạng.
Đáp án đúng là: B.
Ví dụ 12: Gọi ![]() Khi đó S20 có giá trị là
Khi đó S20 có giá trị là
A. 34
B. 30,5
C. 325
D. 32,5
Bài giải:
Ta có:
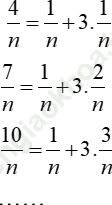
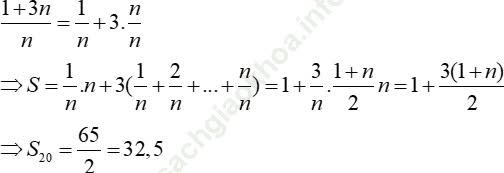
Đáp án đúng là: D
Ví dụ 13: Cho cấp số cộng (un) có công sai d = 1 và u22 − 2u32 − u42 đạt giá trị lớn nhất. Tính tổng S20 của 20 số hạng đầu tiên của cấp số cộng đó.
A. 120
B. 125
C. 130
D. 135
Bài giải:
Đặt a = u1 thì: 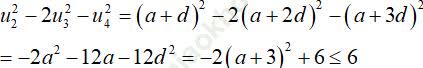 với mọi a.
với mọi a.
Dấu "=" xảy ra khi a + 3 = 0 ⇔ a = − 3.
Suy ra u1 = − 3.
Ta có: 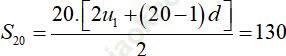 .
.
Đáp án đúng là: C.
C. Bài tập trắc nghiệm
Câu 1: Cho cấp số cộng: − 4; − 8; − 12; − 16... Tìm công sai của cấp số cộng và tổng của 10 số hạng đầu tiên?
A. 110
B. -220
C. 220
D. -110
Đáp án: B
Ta có: − 16 − (− 12) = − 12 − (− 8) = − 8 − (− 4) = − 4
Nên công sai d = − 4
Áp dụng công thức
Câu 2: Cho dãy số (un) có d = 1; S5 = 65. Tính u2?
A. 12
B. 13
C. 14
D. 10
Đáp án: A
Ta có:
=> u1 + u5 = 26 (1)
Lại có: u5 = u1 + 4d = u1 + 4
=> u5 − u1 = 4 (2)
Từ (1) và (2) ta có hệ phương trình:
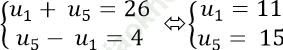
Số hạng thứ hai của dãy số là: u2 = u1 + d = 11 + 1 = 12
Câu 3: Cho cấp số cộng (un) thỏa mãn ![]() . Tính S = u1 + u4 + u7 +.. + u2011.
. Tính S = u1 + u4 + u7 +.. + u2011.
A. S = 2023 736
B. S = 2534134
C. S = 673044
D. S = 2198 650
Đáp án: A
* Gọi d là công sai của cấp số cộng, theo giả thiết ta có:
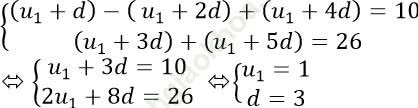
Ta có công sai d = 3 và số hạng đầu u1 = 1.
* Ta có các số hạng u1; u4; u7;... ; u2011 lập thành một cấp số cộng gồm:
nên ta có:
Câu 4: Cho cấp số cộng (un) thỏa mãn: ![]() . Tính tổng 20 số hạng đầu của cấp số cộng là:
. Tính tổng 20 số hạng đầu của cấp số cộng là:
A. − 565
B. − 530
C. − 652
D. − 285
Đáp án: B
* Từ giả thiết bài toán, ta có:
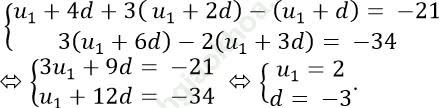
Tổng của 20 số hạng đầu:
Câu 5: Cho cấp số cộng (un) thỏa mãn![]() . Tính tổng
S= u5 + u7 +.. + u2011
. Tính tổng
S= u5 + u7 +.. + u2011
A. S = 3028760
B. S = 3420198
C. S = 3034088
D. S = 3298701
Đáp án: C
* Theo giả thiết ta có:
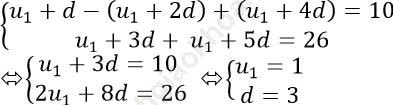
=> Số hạng thứ 5 là: u5 = u1 + 4d = 1 + 4.3 = 13
* Ta có u5; u7.. ,u2011 lập thành cấp số cộng với công sai d' = 2d = 6 và có
Câu 6: Cho cấp số cộng (un) thỏa mãn: 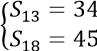 . Tìm số hạng đầu của cấp số cộng.
. Tìm số hạng đầu của cấp số cộng.

Đáp án: A
Theo giả thiết ta có:
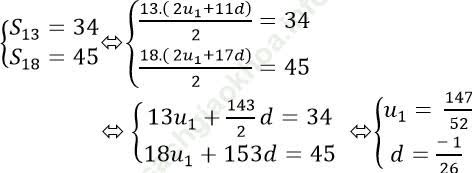
Vậy số hạng đầu tiên của cấp số cộng là:
Câu 7: Cho (un) là cấp số cộng thỏa mãn: ![]() . Tìm số hạng thứ 5 của cấp số cộng.
. Tìm số hạng thứ 5 của cấp số cộng.
A. 10
B. 5
C. 8
D. 0
Đáp án: D
Theo giả thiết ta có:
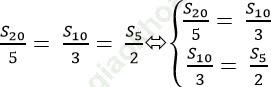
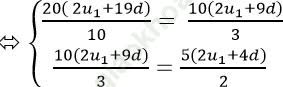
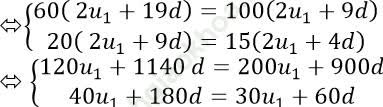
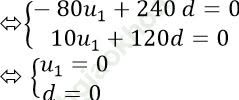
=> Số hạng thứ 5 của cấp số cộng là: u5 = u1 + 4d = 0
Câu 8: Cho (un) là cấp số cộng thỏa mãn: u2 + u22 = 20. Tính S23?
A. 120
B. 230
C. 150
D. 200
Đáp án: B
Theo giả thiết thì u2 + u22 = 20
⇔ u1 + d + u1 + 21d = 20
⇔ 2u1 + 22d = 20
Lại có:
Câu 9: Cho (un) là cấp số cộng thỏa mãn: u21 + u59 = 30. Tính u20 + u59 + u158 + 3u1
A. 90
B. 120
C. 150
D. 180
Đáp án: A
* Theo giả thiết ta có: u1 + u59 = 30
⇔ u1 + 20d+ u1 + 58d = 30
⇔ 2u1 + 78d = 30
* Do đó; u20 + u59 + u158 + 3u1
= u1 + 19d + u1 + 58d + u1 + 157d + 3u1
= 6u1 + 234 = 3. (2u1 + 78d) = 3.30 = 90.
Câu 10: Cho (un) là cấp số cộng. Đặt Sn = m; Sn = m với (m ≠ n). Tính Sm+n
A. – m- n
B. n+ m
C. 2n+2m
D. n. m
Đáp án: A
Ta có Sm = n nên
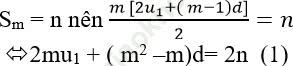
Tương tự do Sn = m nên: 2nu1 + (n2 − n)d = 2m
Từ (1) và (2) vế trừ vế ta được:
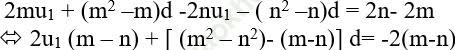
Do m ≠ n nên:
Mặt khác ta có:
Thay kết quả (*) vào biểu thức của Sm+n ta được:
Câu 11: Tính tổng sau: S = 1002 − 992 + 982 − 972 +.. + 22 − 12
A. 5000
B. 5050
C. 5100
D. 5150
Đáp án: B
Ta có:
S = 1002 – 992 + 982 – 972 +... + 22 - 12
⇔ S = (100 - 99). (100+ 99)+ (98- 97). (98+ 97)+... + (2-1)(2+ 1)
⇔ S = 199 + 195 + 191+... + 3
Ta có dãy số 199,195,191,.. , 3 là cấp số cộng với công sai d = -4, số hạng đầu tiên u1 = 199 và có
Vậy tổng
Câu 12: Cho cấp số cộng có tổng của n số hạng đầu tiên được tính bởi công thức Sn = 4n − n2. Gọi M là tổng của số hạng đầu tiên và công sai của cấp số cộng đó. Khi đó:
A. M = 7
B. M= 4
C. M=- 1
D. M= 1
Đáp án: D
Ta có:
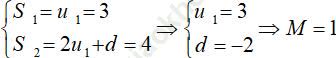
Câu 13: Người ta trồng 3003 cây theo hình một tam giác như sau: hàng thứ nhất có 1 cây; hàng thứ 2 có 2 cây; hàng thứ 3 có 3 cây... hỏi có bao nhiêu hàng?
A. 76
B. 77
C. 78
D. 79
Đáp án: B
Gọi số hàng cây là n.
Gọi số cây lần lượt trên các hàng là 1; 2; 3.. ;n.
Đây là một cấp số cộng với số hạng đầu u1 = 1; d = 1.
Ta có:
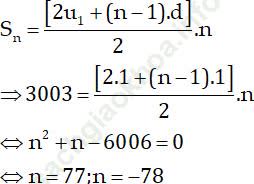
Vậy số hàng cần tìm là 77.