Dạng 3: Tính đơn điệu, tính bị chặn của dãy số - Chuyên đề Toán 11

A. Phương pháp giải & Ví dụ

1. Dãy số tăng, dãy số giảm

♦ Dãy số (u_n) gọi là dãy tăng nếu: u_n < u_n+1 ∀ n ∈ ¥

♦ Dãy số (u_n) gọi là dãy giảm nếu: u_n > u_n+1 ∀ n ∈ ¥

2. Dãy số bị chặn

♦ Dãy số (u_n) gọi là dãy bị chặn trên nếu tồn tại một số thực sao cho u_n < M ∀ n ∈ ¥.

♦ Dãy số (u_n) gọi là dãy bị chặn dưới nếu có một số thực sao cho u_n > m∀ n ∈ ¥..

♦ Dãy số vừa bị chặn trên vừa bị chặn dưới gọi là dãy bị chặn, tức là tồn tại số thực dương M sao cho |u_n | < M ∀ n ∈ ¥..

♦ Để xét tính đơn điệu của dãy số (u_n) ta xét: k_n = (u_n+1 - u_n)

* Nếu k_n > 0∀ n ∈ ¥ ⇒ dãy (u_n) tăng

* Nếu k_n < 0∀ n ∈ ¥ ⇒ dãy (u_n) giảm.

Khi u_n > 0 ∀ n ∈ ¥ ta có thể xét:

* Nếu t_n > 1 ⇒ dãy số (u_n) tăng

* Nếu t_n < 1 ⇒ dãy số (u_n) giảm

♦ Để xét tính bị chặn của dãy số ta có thể dự đoán rồi chứng minh bằng quy nạp.

Ví dụ minh họa

Bài 1: Cho dãy số (u_n). Chứng minh rằng dãy u_n là dãy giảm và bị chặn.

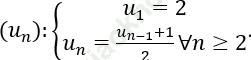
Bài giải:

Để chứng minh dãy (u_n) giảm ta chứng minh u_n > 1, ∀ n ≥ 1

Thật vậy:

Với n = 1 ⇒ u₁ = 2 > 1

Theo nguyên lí quy nạp ta có u_n > 1 ∀ n ≥ 1

Suy ra u_n - u_n-1 < 0

⇔ u_n < u_n-1 ∀ n ≥ 2 hay dãy (u_n) giảm

Theo chứng minh trên, ta có: 1 < u_n < u₁ = 2∀ n ≥ 1

=> Dãy (u_n) là dãy bị chặn.

Bài 2: Cho dãy số (u_n). Chứng minh rằng dãy (u_n) là dãy tăng và bị chặn

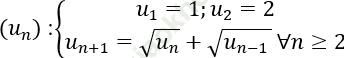
Bài giải:

Ta chứng minh dãy (u_n) là dãy tăng bằng phương pháp quy nạp

* Ta thấy: u₁ < u₂ < u₃.

* Giả sử u_k-1 < u_k ∀ k ≥ 2, ta chứng minh u_k+1 > u_k.

Vậy (u_n) là dãy tăng.

Cũng bằng quy nạp ta chứng minh được u_n < 4 ∀ n, hơn nữa u_n > 0

=> Dãy (u_n) là dãy bị chặn.

B. Bài tập vận dụng

Bài 1: Xét tính tăng giảm của các dãy số sau

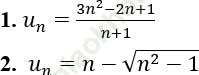
Bài giải:

1. Ta có: nên dãy (u_n) là dãy tăng

2. Ta có: => Dãy (u_n) giảm.

Bài 2: Xét tính tăng, giảm và bị chặn của dãy số (u_n), biết:

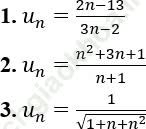
Bài giải:

1. Ta có:

với mọi n ≥ 1.

Suy ra u_(n+1) > u_n ∀ n ≥ 1 ⇒ dãy (u_n) là dãy tăng.

Mặt khác:

Vậy dãy (u_n) là dãy bị chặn.

2. Ta có:

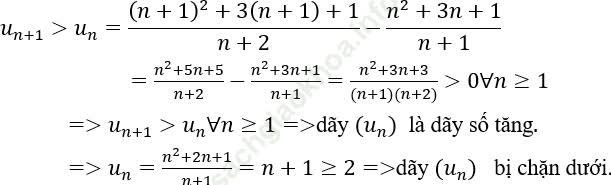
3. Ta có: u_n > 0 ∀ n ≥ 1

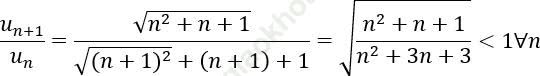
⇒ u_(n+1) < u_n ∀ n ≥ 1 ⇒ dãy (u_n) là dãy số giảm.

Mặt khác: 0 < u_n < 1 ⇒ dãy (u_n) là dãy bị chặn.

Bài 3: Cho dãy số (u_n):

a) Khi a = 4, hãy tìm 5 số hạng đầu của dãy

b) Tìm a để dãy số đã cho là dãy số tăng.

Bài giải:

a) Với a = 4 ta có:

Ta có: 5 số hạng đầu của dãy là u₁=6; u₂=10/3; u₃=14/5; u₄=18/7; u₅=22/9.

b) Ta có dãy số u_n tăng khi và chỉ khi

⇒ - a - 4 > 0 ⇒ a < - 4

Bài 4: Cho dãy số

a) Viết 6 số hạng đầu của dãy

b) Chứng minh: u_n = 3^{(n - 1)} + 1; n = 1,2…

Bài giải:

a) Ta có: u₁ = 2; u₂ = 4; u₃ = 10; u₄ = 28; u₅ = 82; u₆ = 244.

b) Chứng minh bài toán bằng phương pháp quy nạp hoặc chứng minh bằng cách sau:

Ta có: u_n - 1 = 3 (u_{(n - 1)} - 1) = 3² (u_{(n - 2)} - 1) = ⋯ = 3^{(n - 1)} (u₁ - 1)

Suy ra: u_n - 1 = 3^{(n - 1)} ⇒ u_n = 1 + 3^{(n - 1)}.

Bài 5: Cho dãy số u_n = -5^{(n - 1)} + 3ⁿ + n + 2; n = 1,2…

a) Viết 5 số hạng đầu của dãy

b) Chứng minh rằng: u_n = 2u_{(n - 1)} + 3^{(n - 1)} - n.

Bài giải:

Với mọi n =

Suy ra u_n < u₀ - n + 1 = 2012 - n

Do đó: 2011 – n < u_n < 2012 - n

⇒ [u_n] = 2011 - n với n =

Ta có: u₀ = 2011 và

Nên [u₀] = 2011 - 0, [u₁] = 2011 - 1

Vậy [u_n] = 2011 - n, n =