Đạo hàm và bài toán giải phương trình, bất phương trình lượng giác - Chuyên đề Toán 11
A. Phương pháp giải
+ Bước 1: Tính đạo hàm của hàm số.
+ Bước 2: Thiết lập phương trình; bất phương trình.
+ Bước 3: Áp dụng cách giải phương trình; bất phương trình lượng giác đã được học.
B. Ví dụ minh họa
Ví dụ 1. Cho f (x) = sin 2x. Giải phương trình f' (x)=0?

Bài giải:
+ Ta có đạo hàm: f' (x) = 2cos2x
+ Để f' (x) = 0
⇔ 2. cos2x = 0 hay cos2x = 0

Ví dụ 2. Cho hàm số: y = tan (x + π/3). Giải bất phương trình y’ > 0.
A. x ≠ π/6 + kπ
B. x ≠ π/6 + k2π
C. x ≠ π/3 + kπ
D. Tất cả sai
Bài giải:
+ Điều kiện: x + π/3 ≠ π/2 + kπ hay x ≠ π/6 + kπ
+ Với mọi x thỏa mãn điều kiện xác định ta có đạo hàm:
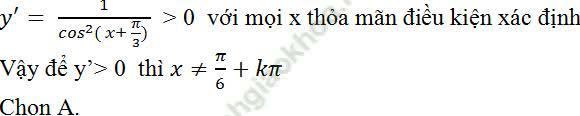
Ví dụ 3. Cho hàm số: y = sinx + cosx. Tìm nghiệm của phương trình y' = 0

Bài giải:
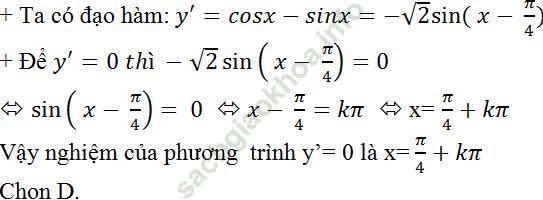
Ví du 4. Cho hàm số: y = tanx + cot x. Giải phương trình y' = 0

Bài giải:
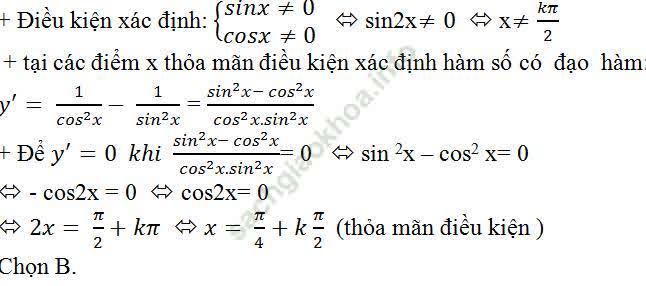
Ví du 5. Cho hàm số: y = 2 cos (2x - π/3). Giải phương trình y' = 4

Bài giải:
Đạo hàm của hàm số đã cho:
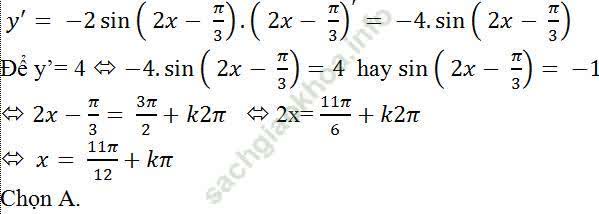
Ví dụ 6 Cho hàm số y = x + sin 2x. Giải phương trình y' = 0

Bài giải:
Đạo hàm của hàm số là: y' = 1 + 2cos2x
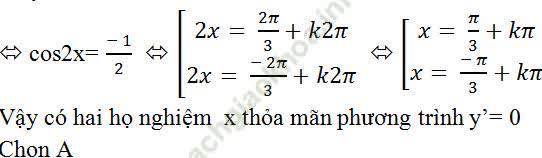
Ví dụ 7.Cho hàm số y = 3x + 1 – cos2x. Tập nghiệm của bất phương trình y' > 0

Bài giải:
Hàm số đã cho xác định với mọi x.
Ta có đạo hàm: y' = 3 + 2sin2x
Với mọi x ta luôn có: - 1 ≤ sin2x ≤ 1 ⇔ - 2 ≤ 2sin2x ≤ 2
⇔ ≤ 3 + 2sin2x ≤ 5
⇒ Với mọi x ta luôn có: y'> 0
Vậy tập nghiệm của bất phương trình là R.
Chọn D.
Ví dụ 8. Cho hàm số y=x3+ 3x+ sin3 x. Giải bất phương trình y' ≥ 0

Bài giải:
Ta có đạo hàm: y' = 3x2 + 3 + 3sin2x. cosx
Với mọi x ta có; cosx ≥ - 1 ⇒ 3sin2 x. cosx ≥ - 3. sin2 x
⇒ 3 + 3sin2x. cosx ≥ 3 - 3. sin2 x
⇔ 3 + 3sin2x. cosx ≥ 3. cos2x (1)
Lại có: 3x2 ≥ 0 ∀ x (2)
Từ (1) và (2) vế cộng vế ta có:
y' = 3x2 + 3 + 3sin2x. cosx ≥ 3x2 + 3cos2 x ≥ 0 với mọi x.
Vậy với mọi x ta luôn có: y' ≥ 0
Đáp án đúng là: C.
Ví dụ 9. Cho hàm số y = cos (2π/3 + 2x). Khi đó phương trình y' = 0 có nghiệm là:

Bài giải:
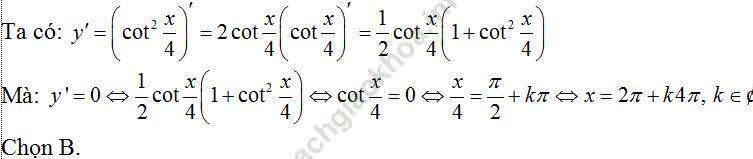
Ví dụ 10. Cho hàm số y = cot2 π/4. Khi đó nghiệm của phương trình y' = 0 là:
Bài giải:
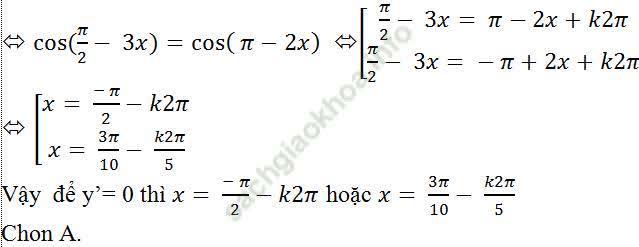
Ví dụ 11.Cho hàm số: y = 2cos3x- 3sin2x. Giải phương trình y' = 0
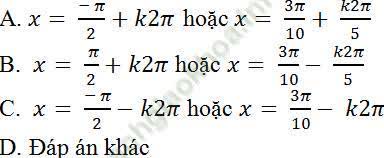
Bài giải:
Ta có: y' = -6 sin3x - 6cos2x
Để y' = 0 thì – 6 sin 3x - 6 cos2x = 0
⇔ sin3x + cos2x = 0
⇔ sin3x = - cos2x
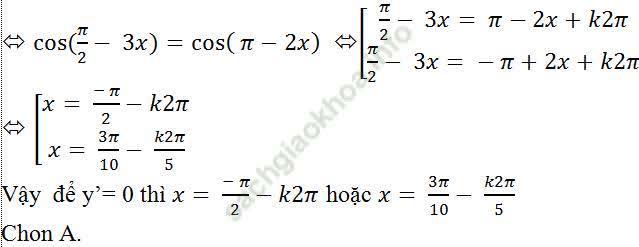
C. Bài tập vận dụng
Câu 1: Cho f (x) = sin (π/2 - 3x). Giải phương trình f' (x) = 0?

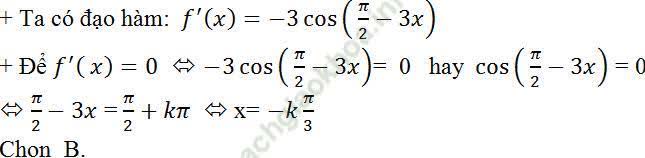
Câu 2: Cho hàm số y = tan (2x + 2π/3). Giải bất phương trình y’ > 0
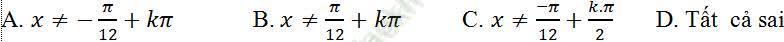
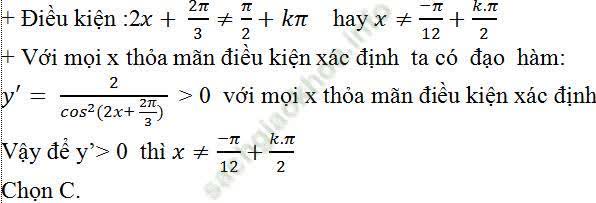
Câu 3: Cho hàm số: y = 2sinx - 2cosx + 10. Tìm nghiệm của phương trình y'=0
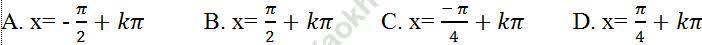
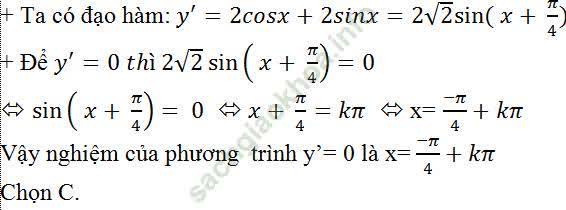
Câu 4: Cho hàm số: y = 2tan3x + 3cot 2x + 90. Giải phương trình y' = 0


Câu 5: Cho hàm số: y= (- 1)/2 cos (4x - π/6). Giải phương trình y' = 1
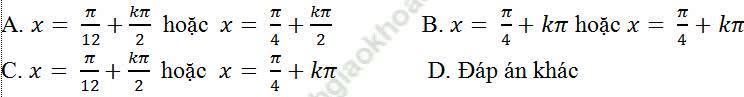
Đạo hàm của hàm số đã cho:
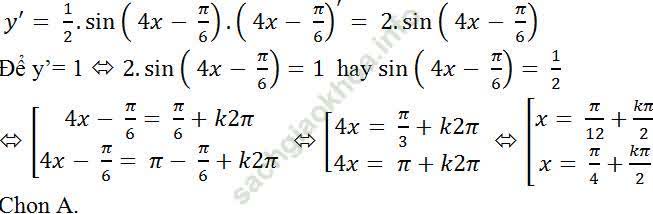
Câu 6: Cho hàm số y = 2x + 1 + cos2x. Giải phương trình y' = 2
A. x = π/3 + kπ
B. x = π/6 + kπ
C. x = kπ/2
D. x = kπ
Đạo hàm của hàm số là: y'=2-2sin2x
Để y^'=2 khi và chỉ khi: 2- 2sin 2x = 2
⇔ sin2x= 0 ⇔ 2x= kπ ⇔ x= kπ/2
Chọn C.
Câu 7: Cho hàm số y = x3 + 3x + sin3x. Tập nghiệm của bất phương trình y^' ≤ 0

Hàm số đã cho xác định với mọi x.
Ta có đạo hàm: y'=3x2+3+3cos3x
Với mọi x ta luôn có: cos3x ≥ -1 nên 3cos3x ≥ -3
⇒ 3+ 3cos3x ≥ 0 (1)
Mà 3x2 ≥ 0 với mọi x. ( 2)
Từ (1) và (2) suy ra; y'=3x2+3+3cos3x ≥ 0
⇒ Để y'≤ 0 khi và chỉ khi 3x2+3+3cos3x=0
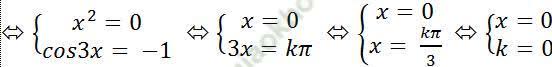
Vậy nghiệm của bất phương trình y'≤ 0 là x= 0
Chọn B. .
Câu 8: Cho hàm số y= x + √x+ sin2 x. Giải bất phương trình y'≥ 0

Điều kiện: x ≥ 0
Taị các điểm x > 0 hàm số đã cho có đạo hàm:
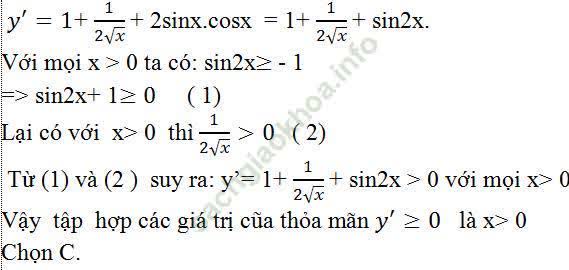
Câu 9: Cho hàm số: y = cos (2x - π/3). sin (2x - π/4). Giải phương trình y’ = 2

Đạo hàm của hàm số đã cho là;
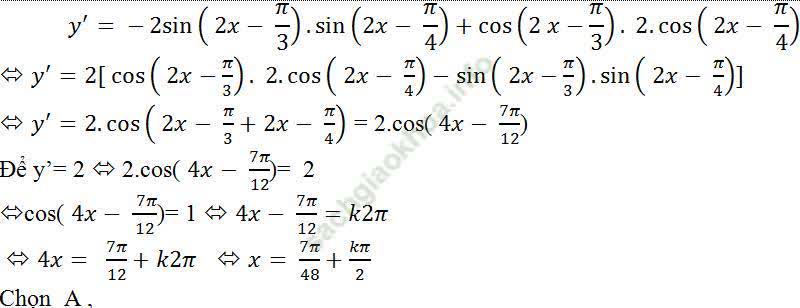
Câu 10: Cho hàm số y = tan (x3 + 3x2+ 3x + 9). Giải phương trình y' = 0?
A. x = 0 B. x = 2 C. x = -1 D. Đáp án khác
+ Điều kiện cos (x3+3x2+3x+9)≠0
+ Tại các điểm x thỏa mãn điều kiện xác định; hàm số có đạo hàm:
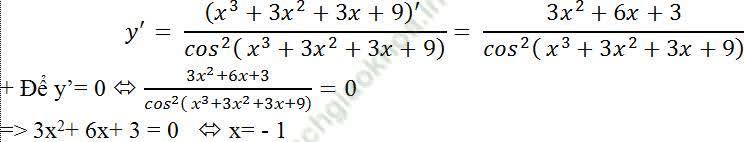
+ Với x= -1 ta có: cos (x3+3x2+3x+9)=cos8≠0 (thỏa mãn điều kiện xác định)
Vậy nghiệm của phương trình y’= 0 là x= - 1