Dạng 1: Phương pháp quy nạp toán học - Chuyên đề Toán 11

A. Phương pháp giải & Ví dụ

Giả sử cần chứng minh đẳng thức: P (n) = Q (n) (hoặc P (n) > Q (n)) đúng với n ≥ n₀, n₀ ∈ ¥ ta thực hiện các bước sau:

Bước 1: Tính P (n₀), Q (n₀) rồi chứng minh P (n₀) = Q (n₀)

Bước 2: Giả sử P (k) = Q (k); k ≥ n₀, k ∈ ¥, ta cần chứng minh P (k+1) = Q (k+1).

Ví dụ minh họa

Bài 1: Chứng minh với mọi số tự nhiên n ≥ 1 ta luôn có: 1 + 2 + 3 +... + n = (n (n + 1))/2

Đặt P (n) = 1 + 2 + 3 +... + n: tổng n số tự nhiên đầu tiên

Ta cần chứng minh: P (n) = Q (n) n ≥ 1, n ∈ ¥.

Bước 1: Với n = 1 ta có P (1) = 1, Q (1) = 1

⇒ P (1) = Q (1) = 1 đúng với n = 1.

Bước 2: Giả sử P (k0 = Q (k) với k ≥ 1, k ∈ ¥. tức là:

Ta cần chứng minh: P (k+1) = Q (k+1), tức là:

Thật vậy:

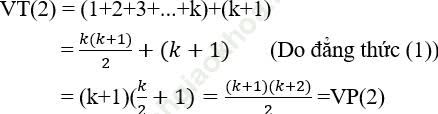
Vậy đẳng thức cho đúng với mọi n ≥ 1.

Bài 2: Chứng minh với mọi số tự nhiên n ≥ 1 ta luôn có: 1 + 3 + 5 + ⋯ + 2n - 1 = n²

♦ Với n = 1 ta có VT = VP = 1

Suy ra đẳng thức cho đúng với n = 1.

♦ Giả sử đẳng thức cho đúng với n = k với k ≥ 1, k ∈ ¥. tức là:

1 + 3 + 5 +⋯+ 2k - 1 = k² (1)

Ta cần chứng minh đẳng thức cho đúng với n = k + 1, tức là:

1 + 3 + 5 +⋯+ (2k - 1) + (2k + 1) = (k + 1)² (2)

Thật vậy: VT (2) = 1 + 3 + 5 +⋯+ (2k - 1) + (2k + 1) = k² + (2k + 1) = (k + 1)² = VP (2)

Vậy đẳng thức cho đúng với mọi n = 1.

Bài 3: Chứng minh rằng vớí ∀ n ≥ 1, ta có bất đẳng thức:

♦ Với n = 1 ta có đẳng thức cho trở thành: 1/2 < 1/√ 3 ⇒ 2 > √ 3 đúng.

⇒ Đẳng thức cho đúng với n = 1.

♦ Giả sử đẳng thức cho đúng với n = k ≥ 1, tức là:

Ta phải chứng minh đẳng thức cho đúng với n = k+1, tức là:

Thật vậy, ta có:

Ta chứng minh:

⇔ (2k+1)(2k+3) < (2k+2)²

⇒ 3 > 1 (luôn đúng)

Vậy đẳng thức cho đúng với mọi số tự nhiên n ≥ 1.

Lưu ý: Phương pháp quy nạp toán học còn được ứng dụng nhiều trong số học và hình học.

B. Bài tập vận dụng

Bài 1: Chứng minh rằng với mọi số tự nhiên n ≥ 1, ta luôn có:

Bài giải:

Bước 1: Với n = 1 ta có: VT = 1; VP = 1 ⇒ VT=VP

⇒ Đẳng thức cho đúng với n = 1.

Bước 2: Giả sử đẳng thức cho đúng với n = k ≥ 1, tức là:

Ta sẽ chứng minh đẳng thức cho đúng với n = k + 1, tức là cần chứng minh

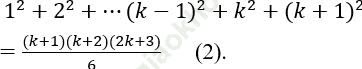
Thật vậy:

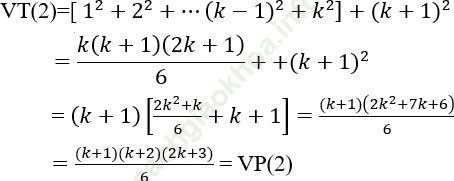
⇒ (1) đúng đẳng thức cho đúng với mọi n ≥ 1.

Bài 2: Chứng minh các đẳng thức sau:

Bài giải:

Bài 3: Chứng minh rằng với mọi n ≥ 1 ta có bất đẳng thức: |sinnx| ≤ k|sinx| ∀ x ∈ I

Bài giải:

Làm tương tự câu 1. Với n = 1 đẳng thức cho đúng

Hướng dẫn:

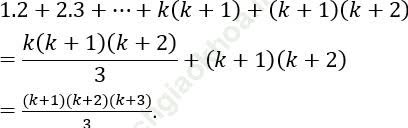
* Với n = 1 ta có: VT = |sin1. α | = 1. |sinα | = VP nên đẳng thức cho đúng.

* Giả sử đẳng thức cho đúng với n = k + 1, tức là: |sinkα | ≤ k|sinα | (1)

Ta phải chứng minh đẳng thức cho đúng với n = k + 1, tức là:

|sin⁡ (k+1)α | ≤ (k+1)|sinα | (2)

Thật vậy:

|sin⁡ (k + 1)α | = |sinkα. cosα + coskα. sinα | ≤ |sinkα ||cosα | + |coskα ||sinα | ≤ |sinkα |+|sinα | ≤ k|sinα |+|sinα | ≤ (k+1)|sinα |

Vậy đẳng thức cho đúng với n = k + 1, nên đẳng thức cho cũng đúng với mọi số nguyên dương n.

Bài 4: Chứng minh rằng với mọi số tự nhiên n ≥ 1 thì A (n) = 7ⁿ + 3n - 1 luôn chia hết cho 9.

Bài giải:

* Với n = 1 ⇒ A (1) = 7¹ + 3.1 - 1 = 9 ⇒ A (1)chia hết cho 9

* Giả sử A (k)chia hết cho 9 ∀ k ≥ 1, ta chứng minh A (k + 1) chia hết cho 9

Thật vậy: A (k + 1) = 7^k+1 + 3 (k+1)1 = 7.7^k + 21k - 7 - 18k + 9

⇒ A (k + 1) = 7A (k) - 9 (2k - 1)

Vì A (k) chia hết cho 9 và 9 (2k - 1) chia hết cho 9 nên A (2k + 1) chia hết cho 9

Vậy A (n) chia hết cho 9 với mọi số tự nhiên n ≥ 1.

Bài 5: Chứng minh rằng tổng các trong một n – giác lồi (n ≥ 1) bằng (n - 2)180º.

Bài giải:

* Với n = 3 ta có tổng ba góc trong tam giác bằng 180º

* Giả sử công thức đúng cho tất cả k-giác, với k < n, ta phải chứng minh mệnh đề cũng đúng cho n-giác. Ta có thể chia n-giác bằng một đường chéo thành ra hai đa giác. Nếu số cạnh của một đa giác là k+1, thì số cạnh của đa giác kia là n – k + 1, hơn nữa cả hai số này đều nhỏ hơn n. Theo giả thiết quy nạp tổng các góc của hai đa giác này lần lượt là. (k-1)180º và (n-k-1)180º

Tổng các góc của n-giác bằng tổng các góc của hai đa giác trên, nghĩa là:

(k - 1 + n - k - 1)180º = (n - 2)180º.

Suy ra mệnh đề đúng với mọi n ≥ 3..