Phương trình thuần nhất bậc 2 đối với sinx và cosx - Chuyên đề Toán 11
A. Phương pháp giải
+ Phương trình thuần nhất bậc hai đối với sinx và cosx là phương trình có dạng:
a. sin2 x+ b. sinx. cosx + c. cos2 x= 0 (1)
Trong đó a; b và c là các số đã cho với a ≠ 0 hoặc b ≠ 0 hoặc c ≠ 0
+ Có hai cách để giải phương trình thuần nhất bậc hai đối với sinx và cosx:
* Cách 1:
Bước 1: Kiểm tra cosx = 0 có nghiệm của phương trình.
Lưu ý: cosx = 0 ⇒ sin2 x = 1
Bước 2. Nếu cosx ≠ 0 chia cả hai vế của phương trình cho cos2x. Khi đó phương trình đã cho có dạng: a. tan2 x+ b. tanx+ c= 0
Đây là phương trình bậc hai ẩn tanx. Giải phương trình ta tính được tanx
⇒ x=....
Lưu ý:
* Cách 2: Áp dụng công thức hạ bậc; công thức nhân đôi ta có:
a. sin2 x+ b. sinx. cosx+ c. cos2 x= 0
⇒ b. sin2x+ (c-a) cos2x = - a- c
Đây là phương trình bậc nhất đối với sinx và cosx
B. Ví dụ minh họa
Ví dụ 1. Giải phương trình: ![]()
A. ![]()
B. ![]()
C. ![]()
D. Vô nghiệm
Bài giải:
Đáp án đúng là: D.
Hướng dẫn:
+ Trường hợp 1.
Thay cosx = 0 vào phương trình đã cho ta thấy không thỏa mãn.
+ Trường hợp 2. Với cosx ≠ 0
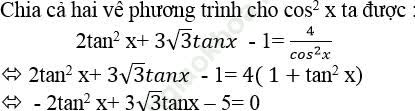
Phương trình này vô nghiệm
⇒ Phương trình đã cho vô nghiệm.
Ví dụ 2: Phương trình: ![]() có các nghiệm là:
có các nghiệm là:
A. 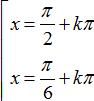
B. 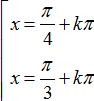
C. 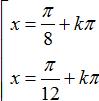
D. 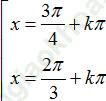
Bài giải:
Đáp án đúng là: A
Hướng dẫn:
Trường hợp 1.
- Nếu cosx = 0 ⇒ sin2x = 1 thay vào phương trình đã cho ta được:
6.1 + 0 – 0 = 6 (luôn đúng)
⇒ Phương trình có nghiệm x = π/2 + kπ
Trường hợp 2.
- Nếu cos x ≠ 0 chia cả hai vế cho cos2 x ta được
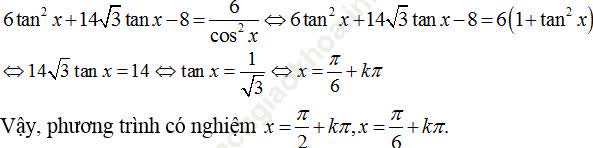
Ví dụ 3. Cho phương trình 2sin2 x – 5sinx. cosx +3cos2 x= 0. Tìm một họ nghiệm của phương trình:
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Bài giải:
Đáp án đúng là: C
Hướng dẫn:
Trường hợp 1:
- Nếu cosx = 0 ⇒ sin2 x = 1 thay vào phương trình đã cho ta thấy không thỏa mãn.
Trường hợp 2:
- Nếu cosx ≠ 0. Chia cả hai vế của phương trình cho cos2 x ta được:
2tan2 x – 5tanx + 3= 0
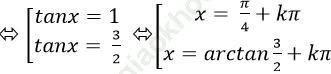
Ví dụ 4. Giải phương trình: 4sin2 x+4sinx. cosx+ cos2x= 0.
A. ![]()
B. x= arctan (-2)+kπ
C. ![]()
D. x= arctan2+kπ
Bài giải:
Đáp án đúng là: C.
Hướng dẫn:
- Trường hợp 1.
Nếu cosx = 0 ⇒ sin2 x = 1 thay vào phương trình đã cho ta thấy không thỏa mãn.
- Trường hợp 2:
Nếu cosx ≠ 0. Chia cả hai vế phương trình cho cos2 x ta được:
4tan2 x + 4tanx + 1 = 0
⇒ (2tanx + 1)2 = 0
⇒ 2tanx + 1 = 0
⇒ tan x = (-1)/2
⇒ x = arctan (- 1)/2 + kπ
Ví dụ 5. Phương trình:
![]() có các nghiệm là:
có các nghiệm là:
A. 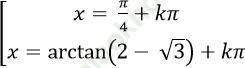
B. 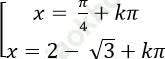
C. 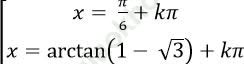
D. Tất cả sai
Bài giải:
Đáp án đúng là: A.
Hướng dẫn:
+ Trường hợp 1: Nếu cosx= 0 ⇒ sin2x = 1 thay vào phương trình đã cho ta thấy không thỏa mãn
+ Trường hợp 2: Nếu cosx ≠ 0 ta chia cả hai vế của phương trình cho cos2 ta được:
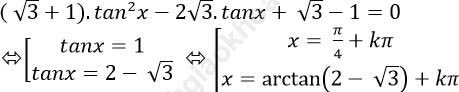
Ví dụ 6: Giải phương trình - 3sin2x – 2sinx. cosx + 4cos2 x= - 3
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Bài giải:
Đáp án đúng là: A.
Hướng dẫn:
- Trường hợp 1. Nếu cosx = 0 ⇒ sin2 x = 1 thay vào phương trình đã cho ta thấy không thỏa mãn.
- Trường hợp 2. Nếu cosx ≠ 0. Chia hai vế phương trình cho os2 x ta được:
- 3tan2 x - 2tanx + 4= (- 3)/ (cos2 x)
⇒ - 3tan2 x – 2tanx + 4 = - 3 (1 + tan2 x)
⇒ - 2tanx = -7
⇒ tanx = 7/2
⇒ x = arctan 7/2 + kπ
Ví dụ 7: Phương trình 2sin2 x + sinx. cosx – cos2 x = 0 có nghiệm là:
A. 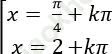
B. 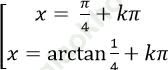
C. 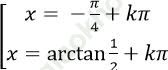
D. 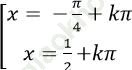
Bài giải:
Đáp án đúng là: C.
- Trường hợp 1. Nếu cosx = 0 ⇒ sin2 x = 1 thay vào phương trình ta thấy không thỏa mãn.
- Trường hợp 2. Nếu cosx ≠ 0; chia cả hai vế của phương trình cho cos2 x ta được:
2tan2 x+ tanx – 1 = 0
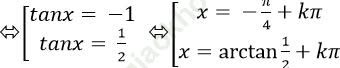
Ví dụ 8: Một họ nghiệm của phương trình: 2sin2x - 5sinx. cosx – cos2 x = - 2 là:
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Bài giải:
Đáp án đúng là: B.
Hướng dẫn:
- Trường hợp 1: Nếu cosx = 0 ⇒ sin2 x = 1 thay vào phương trình đã cho ta thấy không thỏa mãn.
- Trường hợp 2. Nếu cosx ≠ 0 chia cả hai vế cho cos2 x ta được:
2 tan2x – 5 tanx - 1 = (- 2)/ (cos2 x)
⇒ 2tan2 x – 5tanx – 1 = - 2 (1 + tan2x)
⇒ 2tan2x – 5tanx - 1 = - 2 – 2tan2 x
⇒ 4tan2 x – 5tanx + 1 = 0
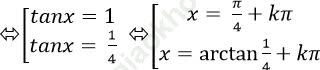
Ví dụ 9. Cho phương trình: 2sin2 x - 4sinx. cosx + 4 cos2x = m. Tìm điều kiện của m để phương trình đã cho có nghiệm
A. 1 < m hoặc m < - 1
B. m > √ 3 hoặc m < - √ 5
C. 2- √ 5 ≤ m ≤ 2+ √ 5
D. Đáp án khác
Bài giải:
Đáp án đúng là: C.
Hướng dẫn:
Áp dụng công thức hạ bậc và công thức nhân đôi ta có:
2sin2 x - 4sinx. cosx + 4cos2 x = m
⇒ (1 - cos2x) - 2sin2x + 2cos2x + 1 = m
⇒ cos2x – 2sin2x = m - 2
Đây là phương trình bậc nhất đối với sin2x và cos2x nên điều kiện để phương trình có nghiệm là: 12 + (-2)2 ≥ (m-2)2
⇒ 5 ≥ m2 - 4m+ 4 ⇒ m2 – 4m - 1 ≤ 0
⇒ 2- √ 5 ≤ m ≤ 2+ √ 5
Ví dụ 10: Giải phương trình 4sin3 x + 3cos3x - 3sinx – sin2x. cosx = 0
A. 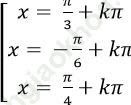
B. 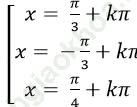
C. 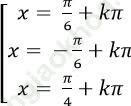
D. Đáp án khác
Bài giải:
Đáp án đúng là: B.
Hướng dẫn:
- Trường hợp 1. Nếu cosx = 0 ⇒ sin2 x= 1 thay vào phương trình đã cho ta thấy không thỏa mãn.
- Trường hợp 2. Nếu cosx ≠ 0. Chia cả hai vế cho cos3 x ta được:
⇒ 4. tan3 x+ 3- 3tanx. (1+ tan2 x) – tan2x = 0
⇒ 4. tan3 x + 3- 3tanx – 3tan3x – tan2 x = 0
⇒ tan3 x – tan2 x - 3tanx + 3= 0
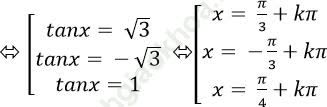
Ví dụ 11: Giải phương trình 2cos3x = sin3x
A. 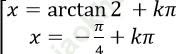
B. 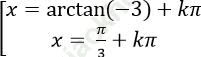
C. 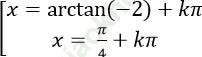
D. 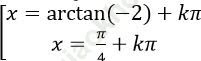
Bài giải:
Đáp án đúng là: C.
Hướng dẫn:
Ta có: 2cos3x = sin3x
⇒ 2cos3 x = 3sinx - 4sin3x
Ta thấy cosx = 0 không là nghiệm của phương trình đã cho. Chia cả hai vế phương trình cho cos3 x ta được:
⇒ 2 = 3. tanx (1 + tan2 x) – 4tan3 x
⇒ 2 = 3tanx + 3tan3x – 4tan3x
⇒ tan3x – 3tanx + 2 = 0
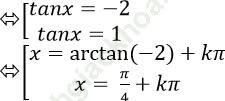
Ví dụ 12: Giải phương trình: ![]()
A. 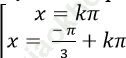
B. 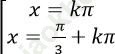
C. 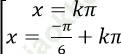
D. Đáp án khác
Bài giải:
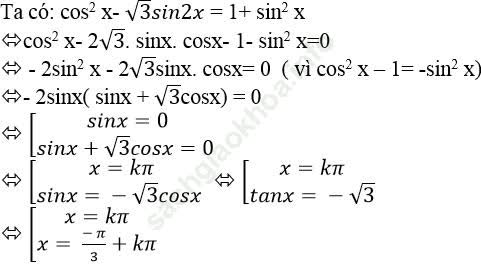
C. Bài tập vận dụng
Câu 1: Giải phương trình 4sin2x + 5sinx. cosx – 9cos2 x = 0
A. 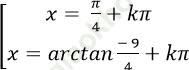
B. 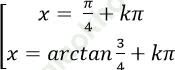
C. 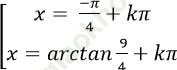
D. 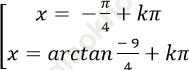
+ Trường hợp 1. Nếu cos x = 0 ⇒ sin2 x= 1
Thay vào phương trình đã cho ta thấy không thỏa mãn
+ Trường hợp 2. Nếu cosx ≠ 0.
Chia cả hai vế cho cos2 x ta được:
4tan2 x + 5tanx – 9=0
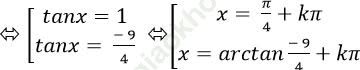
Chọn A.
Câu 2: Giải phương trình – sin2 x – 2sin2x - 4cos2 x = 0
A. x = arctan (-3) + kπ
B. x = arctan 3 + kπ
C. x = arctan 2 + kπ
D. x = arctan (-2) + kπ
+ Trường hợp 1. Nếu cosx = 0 ⇒ sin2 x= 1
Thay vào phương trình đã cho ta thây không thỏa mãn.
+ Trường hợp 2. Nếu cosx ≠ 0.
Ta có: - sin2 x – 2sin2x – 4cos2 x = 0
⇒ -sin2 x – 4sinx. cosx – 4cos2 x= 0
Chia cả hai vế của phương trình cho cos2 x ta được:
- tan2 x – 4tanx – 4= 0
⇒ - (tanx + 2)2 = 0
⇒ tanx +2= 0 ⇒ tanx = - 2
⇒ x = arctan (-2)+ kπ
Chọn D
Câu 3: Giải phương trình: ![]()
A. 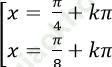
B. 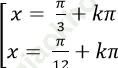
C. 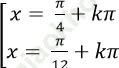
D. 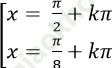
Áp dụng công thức hạ bậc và công thức nhân đôi ta có:
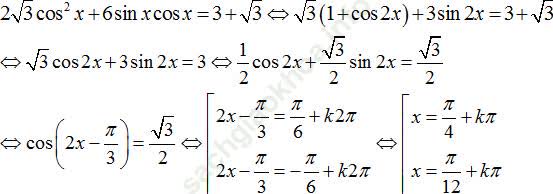
Chọn C.
Câu 4: Một họ nghiệm của phương trình: sin2 x – 3sinx. cosx = 2 là:
A. 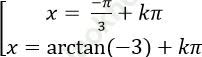
B. 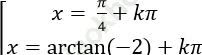
C.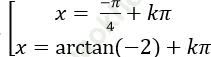
D. Đáp án khác
+ Trường hợp 1. Nếu cosx= 0 ⇒ sin2x= 1 thay vào phương trình đã cho thấy không thỏa mãn.
+ Trường hợp 2. Nếu cosx ≠ 0; chia cả hai vế phương trình cho cos2 x ta được:
tan2 x – 3tanx = 2/ (cos2 x)
⇒ tan2 x -3tanx= 2 (1+tan2 x)
⇒ tan2 x – 3tanx = 2+ 2 tan2 x
⇒ - tan2 x – 3tanx – 2 = 0
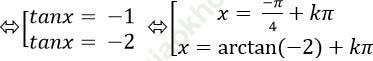
Chọn C.
Câu 5: Giải phương trình 3sin2 x – 4sinx. cosx + 5cos2 x = 2.
A. 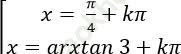
B. 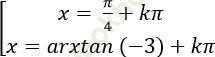
C. 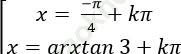
D. 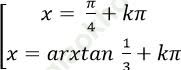
+ trường hợp 1. Nếu cosx=0 ⇒ sin2x= 1 thay vào phương trình đã cho ta thấy không thỏa mãn.
+ Trường hợp 2. Nếu cosx ≠ 0.
Chia cả hai vế của phương trình cho cos2 x ta được:
3tan2 x – 4tan x+ 5= 2/ (cos2 x)
⇒ 3. tan2 x – 4tanx + 5= 2 (1+ tan2 x)
⇒ tan2 x - 4tanx + 3= 0
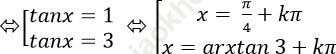
Chọn A
Câu 6: Phương trình: ![]() có nghiệm là
có nghiệm là
A. 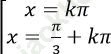
B. 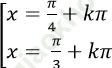
C. 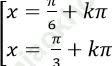
D. 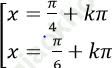
+ Trương hợp 1.
Nếu cosx = 0 ⇒ sin2 x= 1
Thay vào phương trình đã cho ta thấy không thỏa mãn.
+ Trường hợp 2.
Nếu cosx ≠ 0. Chia cả hai vế phương trình cho cos2x ta được:

Chọn B.
Câu 7: Phương trình: ![]() có nghiệm là
có nghiệm là
A. ![]()
B. ![]()
C. ![]()
D. ![]()
+ Trường hợp 1. Nếu cos2x = 0 ⇒ sin2 2x= 1
Thay vào phương trình đã cho ta thấy không thỏa mãn.
+ Trường hợp 2. Nếu cos2x ≠ 0. Chia cả hai vế phương trình cho cos2 2x ta được:
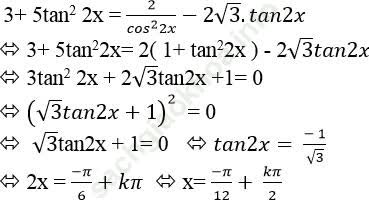
Chọn D
Câu 8:Phương trình: ![]() có một họ nghiệm là
có một họ nghiệm là
A. ![]()
B. ![]()
C. ![]()
D. ![]()
+ Trường hợp 1. Nếu cosx = 0 ⇒ sin2 x= 1
Thay vào phương trình đã cho ta thấy thỏa mãn.
⇒ x= π/2+kπ là nghiệm của phương trình đã cho
+ Trường hợp 2. Nếu cosx ≠ 0

Chọn D.
Câu 9: Giải phương trình sin2x + 3tanx = cosx. ( 4sinx – cosx)
A. ![]()
B. ![]()
C. ![]()
D. Đáp án khác
Điều kiện: cosx ≠ 0
Ta có: sin2 x+ 3tanx =cosx. (4sinx-cosx)
⇒ sin2 x+ 3tanx= 4sinx. cosx- cos2x
Chia cả hai vế cho cos2 x ta được:
⇒ tan2 x+ 3tanx (1+ tan2 x)- 4tanx + 1= 0
⇒ tan2 x + 3tanx + 3tan3 x – 4tanx + 1 = 0
⇒ 3tan3 x + tan2 x – tanx +1= 0
⇒ tanx= - 1
⇒ x= (- π)/4+kπ
Chọn A.
Câu 10: Giải phương trình: sin2 x. ( tanx+ 1) = 3sinx. (cosx – sinx) + 3
A. 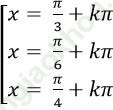
B. 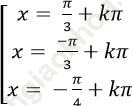
C. 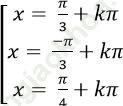
D. Đáp án khác
Điều kiện: cosx ≠ 0.
Ta có: sin2 x. (tanx+ 1) = 3sinx. ( cosx- sinx) + 3
⇒ sin2 x. (tanx+ 1) = 3sinx. cosx – 3sin2 x+ 3
⇒ sin2 x. (tanx+ 1) = 3sinx. cosx + 3cos2 x (vì 3-3sin2 x= 3cos2 x)
Chia cả hai vế phương trình cho cos2 x ≠ 0 ta được:
tan2x. ( tanx+ 1) = 3tanx + 3
⇒ tan2 x. ( tanx+ 1) – (3tanx+ 3)= 0
⇒ tan2 x. (tanx +1)- 3 (tanx+ 1) = 0
⇒ (tan2 x- 3)( tanx+ 1) = 0

Chọn B.