Cách chứng minh bằng phương pháp quy nạp cực hay có lời giải - Chuyên đề Toán 11

A. Phương pháp giải

Để chứng minh một mệnh đề P (n) phụ thuộc vào số tự nhiên n đúng với mọi n ≥ m (m là số tự nhiên cho trước), ta thực hiện theo hai bước sau:

Bước 1: CMR: P (n) đúng khi n = m.

Bước 2: Với k là một số tự nhiên tùy và k ≥ m. Giả sử P (n) đúng khi n = k, ta sẽ chứng minh P (n) cũng đúng khi n = k + 1.

Theo nguyên lý quy nạp toán học, ta đưa ra kết luận rằng P (n) đúng với mọi số tự nhiên n ≥ m.

B. Ví dụ minh họa

Ví dụ 1: Chứng minh rằng với mọi số nguyên dương n, ta có: 1.4 + 2.7 +... + n (3n + 1) = n (n + 1)² (1)

Bài giải:

+ Với n = 1 ta có:

Vế trái = 1.4= 4.

Vế phải = 1. (1+ 1)² = 4.

=> Vế trái = Vế phải. => (1) đúng với n = 1.

+ Giả sử (1) đúng với n= k; k ∈ N*; tức là ta có:

1.4 + 2.7 + ⋅⋅⋅ + k (3k + 1) = k (k + 1)² (2)

Ta chứng minh nó cũng đúng với n = k + 1.

Có nghĩa ta phải chứng minh: 1.4 + 2.7 +⋅⋅⋅+ k (3k + 1) + (k + 1)(3k + 4) = (k + 1)(k + 2)²

+ Thật vậy do 1.4 + 2.7 +... + k. ( 3k + 1) = k (k + 1)² nên

1.4 + 2.7 +⋯+ k (3k + 1) + (k + 1). (3k + 4) = k (k + 1)² + (k + 1)(3k + 4)

= k (k² + 2k + 1) + 3k² + 4k + 3k + 4

= k³ + 2k² + k + 3k² + 7k + 4 = k³ + 5k² + 8k + 4 = (k + 1). (k + 2)²

Do đó (1) đúng với mọi số nguyên dương n.

Ví dụ 2: Chứng ming rằng với mọi số nguyên dương n ta có:

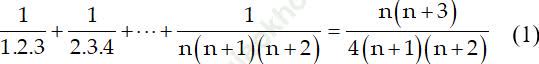
Bài giải:

+ Với n = 1: Vế trái

Vế phải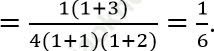

=> Vế trái = Vế phải. => (1) đúng với n = 1.

+ Giả sử (1) đúng với n = k; k ∈ N*. Có nghĩa là ta có:

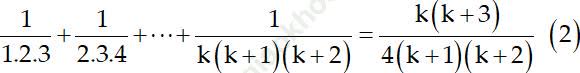
* Ta phải chứng minh (1) đúng với n = k+ 1. Có nghĩa ta phải chứng minh:

* Thật vậy:

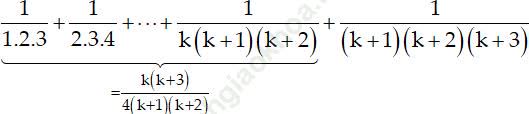
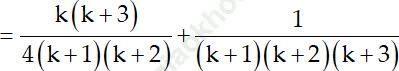
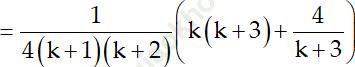
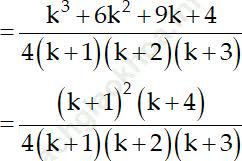
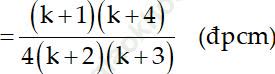
Vậy (1) đúng khi n = k + 1. Do đó (1) đúng với mọi số nguyên dương n.

Ví dụ 3: Với mỗi số nguyên dương n, gọi u_n = 9ⁿ − 1. Chứng minh rằng với mọi số nguyên dương n thì u_n luôn chia hết cho 8.

Bài giải:

+ Với n = 1 ta có u₁ = 9¹ − 1 = 8 chia hết cho 8 (đúng).

+ Giả sử u_k = 9^k − 1 chia hết cho 8 với k ∈ N*

Ta cần chứng minh: u_{k + 1} = 9^k + 1 − 1 chia hết cho 8.

* Thật vậy, ta có u_k+1 = 9^k+1 − 1 = 9.9^k − 1 = 9 (9^k − 1) + 8 = 9u_k + 8.

Vì 9u_k và 8 đều chia hết cho 8

=> u_{k+ 1} = 9^k + 8 ⋮ 8.

Vậy với mọi số nguyên dương n thì u_n chia hết cho 8.

Ví dụ 4: Chứng minh rằng với mọi số tự nhiên n ≥ 2, ta luôn có: 2n + 1 > 2n+ 3 (*)

Bài giải:

+ Với n = 2 ta có: 2^{2 + 1} = 8 và 2.2 + 3 = 7

=> 8 > 7 nên (*) đúng khi n = 2

+ Giả sử với n = k; k ≥ 2 thì (*) đúng, có nghĩa ta có: 2^{k+ 1} > 2k + 3 (1).

Ta phải chứng minh (*) đúng với n = k + 1, có nghĩa ta phải chứng minh:

2^k+2 > 2 (k+1) + 3

* Thật vậy, nhân hai vế của (1) với 2 ta được:

2.2^k+1 > 2 (2k + 3)

⇔ 2^k+2 > 4k + 6 > 2 (k + 1) + 3

Vậy 2^k+2 > 2 (k + 1) + 3 (đúng).

Do đó theo nguyên lí quy nạp, (*) đúng với mọi số nguyên dương n ≥ 2

Ví dụ 5: Chứng minh rằng với mọi số nguyên dương n ta có:

Bài giải:

* Với n = 1:

Vế trái của (1) = 1 và vế phải của (1)

Vậy (1) đúng với n = 1.

* Giả sử (1) đúng với n= k; k ∈ N*. Có nghĩa là ta có:

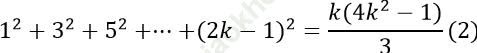
Ta chứng minh (1) đúng với n= k+ 1. Có nghĩa ta phải chứng minh:

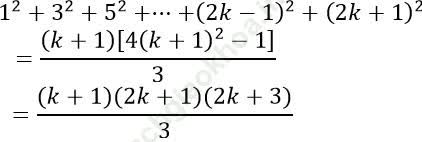
* Thật vậy 1²+3²+5²+⋅⋅⋅+ (2k − 1)²+ (2k+1)² =

+ (2k+1)² (thế (2) vào).

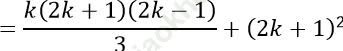
Vậy (1) đúng khi n= k+ 1. Do đó theo nguyên lí quy nạp, (1) đúng với mọi số nguyên dương n.

Ví dụ 6: Chứng minh với mọi số nguyên dương n và n ≥ 5 thì 2ⁿ > n² (*)

Bài giải:

* Với n = 5 ta có: 2⁵ > 5² (vì 32 > 25) (đúng).

Vậy (*) đúng với n = 5.

* Giả sử với n= k; k ≥ 5 thì (*) đúng, có nghĩa ta có: 2^k > k² (1).

Ta phải chứng minh (*) đúng với n = k + 1, có nghĩa ta phải chứng minh: 2^k+1 > (k+1)²

* Thật vậy, nhân hai vế của (1) với 2 ta được:

2.2^k > 2. k² ⇔ 2^k+1 > k² + k²

⇔ 2^k+1 > k² + 2k + 1= (k+1)² (vì k² > 2k+ 1 với mọi k ≥ 5).

Vậy (*) đúng với mọi số nguyên dương n≥5.

Ví dụ 7: Chứng minh với mọi số nguyên n ta có:

Bài giải:

* Với n = 1:

Vế trái của (1) = 1.2= 2,

vế phải của (1)

VT=VP=> (1) Đúng với n= 1.

* Giả sử (1) đúng với n = k; k∈N*. Có nghĩa là ta có:

1.2+2.3+3.4+⋅⋅⋅+k (k+1)=

(2)

* Ta phải chứng minh (1) đúng với n = k + 1. Có nghĩa ta phải chứng minh:

1.2 + 2.3 + 3.4 +⋅⋅⋅+ k (k + 1) + (k + 1)(k + 2) =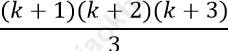

Thật vậy:

1.2 + 2.3 + 3.4 +⋅⋅⋅+ k (k + 1) + (k + 1)(k + 2)

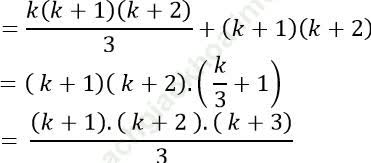
Vậy (1) đúng khi n = k + 1. Do đó theo nguyên lí quy nạp, (1) đúng với mọi số nguyên dương n.

Ví dụ 8: Chứng minh rằng với mọi số nguyên dương n ta có:

1.2 + 2.5 + 3.8 +.. + n (3n − 1) = n²(n + 1) (1)

Bài giải:

* Với n = 1:

Vế trái của (1) = 2, vế phải của (1) = 12. ( 1 + 1) = 2.

Suy ra (1) đúng với n = 1.

* Giả sử (1) đúng với n= k; k ∈ N*. Có nghĩa là ta có:

1.2 + 2.5 + 3.8 +⋅⋅⋅+ k (3k − 1) = k²(k + 1) (2)

Ta phải chứng minh (1) đúng với n = k +1. Có nghĩa ta phải chứng minh:

1.2 + 2.5 + 3.8 +⋅⋅⋅+ k (3k − 1) + (k + 1)(3k + 2) = (k + 1)²(k + 2)

Thật vậy:

1.2 + 2.5 + 3.8 +⋅⋅⋅+ k (3k − 1) + (k + 1)(3k + 2) = k²(k + 1) + (k + 1)(3k + 2)

= (k + 1)(k² + 3k + 2) = (k + 1)(k + 1)(k + 2) = (k + 1)²(k + 2) (đpcm).

Vậy (1) đúng khi n = k + 1. Do đó theo nguyên lí quy nạp, (1) đúng với mọi số nguyên dương n.

Ví dụ 9: Chứng minh với mọi số nguyên dương n ta có: n³ − n chia hết cho 3

Bài giải:

Đặt u_n = n³ − n

* Ta có u₁ = 1³ − 1 = 0 chia hết cho 3

=> Đúng với n = 1.

* Giả sử u_k = k³ − k chia hết cho 3.

Ta cần chứng minh u_k+1 = (k + 1)³ − (k + 1) chia hết cho 3.

* Thật vậy, u_k+1 = k³+ 3k² + 3k + 1 − k − 1 = k³ + 3k² + 2k

⇔ u_{k + 1} = (k³ − k) + (3k² + 3k) = u_k + 3 (k² + k)

Vì u_k và 3 (k² + k) đều chia hết cho 3, nên u_k+1 cũng chia hết cho 3.

Vậy với mọi số nguyên dương n thì u_n chia hết cho 3.

Ví dụ 10: Chứng minh rằng với mọi số nguyên dương n ta có: 2n³ − 3n² + n chia hết cho 6.

Bài giải:

* Đặt u_n = 2n³ − 3n² + n

*Ta có: u₁ = 2.1³ − 3.1² + 1 = 0 chia hết cho 6

=> Đúng với n = 1.

* Giả sử u_k = 2k³ − 3k²+ k chia hết cho 6.

Ta cần chứng minh: u_{k + 1} = 2. (k+1)³ − 3. (k+1)² + k+1 chia hết cho 6.

* Thật vậy ta có: u_k+1 = 2. k³+ 6k² + 6k + 2 − 3k² − 6k − 3 + k + 1

⇔ u_{k + 1} = 2k³ + 3k² + k = 2k³ − 3k² + k + 6k² = u_k + 6k²

Vì u_k và 6k² đều chia hết cho 6, nên u_{k + 1} cũng chia hết cho 6.

Vậy với mọi số nguyên dương n thì u_n chia hết cho 6.

Ví dụ 11: Chứng minh với mọi số nguyên dương n ta có: 13ⁿ − 1 chia hết cho 6.

Bài giải:

* Đặt u_n = 13ⁿ − 1

* Với n = 1, ta có u₁ = 13¹ − 1 = 12 chia hết cho 6

=> Đúng với n = 1.

* Giả sử u_k = 13^k − 1 chia hết cho 6 (với k ∈ N*).

Ta cần chứng minh: u_k+1= 13^k+1 − 1 ⋮ 6.

* Thật vậy ta có: u_k+1 = 13.13^k − 1 = 13 (13^k − 1) + 12 = 13. u_k + 12

Vì 13u_k và 12 đều chia hết cho 6, nên u_{k + 1} cũng chia hết cho 6.

Vậy với mọi số nguyên dương n thì u_n chia hết cho 6.

Ví dụ 12: Chứng minh với mọi số nguyên n và n ≥ 3 thì 3ⁿ > n² + 4n + 5 (*)

Bài giải:

* Với n = 3 ta có 3³ > 3² + 4.3 + 5 ⇔ 27 > 26 (đúng).

Vậy (*) đúng với n = 3.

* Giả sử với n = k; k ≥ 3 thì (*) đúng, có nghĩa ta có: 3^k > k² + 4k + 5 (1).

Ta phải chứng minh (*) đúng với n = k+ 1, có nghĩa ta phải chứng minh:

3^{k + 1} > (k + 1)² + 4 (k + 1) + 5

* Thật vậy, nhân hai vế của (1) với 3 ta được: 3.3^k > 3. k² + 12k + 15

⇔ 3^{k + 1} > (k² + 2k + 1) + 4 (k + 1) + 5 + (2k² + 6k + 5) (2)

Vì (2k² + 6k + 5) > 0 với mọi k ≥ 3 (3)

Từ (2) và (3) suy ra: 3^k+1 > (k² + 2k + 1) + 4 (k + 1) + 5

Hay 3^k+1 > (k + 1)² + 4 (k + 1) + 5

Vậy (*) đúng với mọi số nguyên dương n ≥ 3.

C. Bài tập trắc nghiệm

Câu 1: Chứng minh với mọi số nguyên dương n ta có:

1.2.3 + 2.3.4 + 3.4.5 +.. + n (n+1). (n+2) = (1)

Hiển thị đáp án

*Với n = 1:

Vế trái của (1) = 1.2.3= 6, vế phải của

Suy ra (1) đúng với n = 1.

* Giả sử (1) đúng với n = k; k ∈ N*. Có nghĩa là ta có:

1.2.3+2.3.4+3.4.5+⋅⋅⋅+k (k+1)(k+2) =

(2)

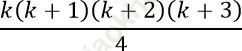
Ta phải chứng minh (1) đúng với n = k+1. Có nghĩa ta phải chứng minh:

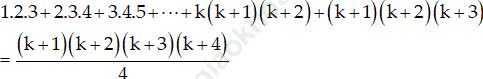
Thật vậy:

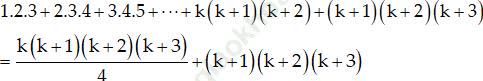
Vậy (1) đúng khi n = k + 1. Do đó theo nguyên lí quy nạp, (1) đúng với mọi số nguyên dương n.

Câu 2: Chứng minh với mọi số nguyên dương n ≥ 2 ta có:

Hiển thị đáp án

*Với n = 2:

Vế trái của

, vế phải của

Suy ra (1) đúng với n = 2.

* Giả sử (1) đúng với n= k.

Có nghĩa là ta có:

Ta chứng minh (1) đúng với n= k + 1. Có nghĩa ta phải chứng minh:

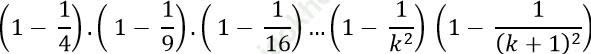
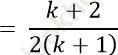
Thật vậy ta có:

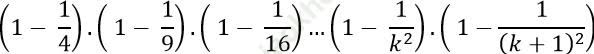
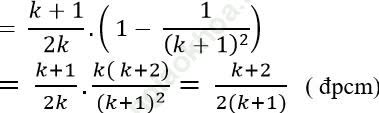
Vậy (1) đúng khi n = k + 1. Do đó theo nguyên lí quy nạp, (1) đúng với mọi số nguyên dương n ≥ 2.

Câu 3: Chứng minh với mọi số nguyên dương n ta có:

Hiển thị đáp án

* Với n = 1:

Vế trái của (1) = 1, vế phải của (1)= 2√ 1 = 2.

Suy ra (1) đúng với n = 1.

* Giả sử (1) đúng với n = k; k ≥ 1

Có nghĩa là ta có:

Ta phải chứng minh (1) đúng với n= k+ 1. Có nghĩa ta phải chứng minh:

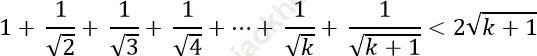
*Thật vậy:

Vì:

⇔ 2√ (k (k+1)) + 1 < 2 (k+1)

⇔ 2√ (k² + k) < 2k+1 ⇔ 4 (k² + k) < (2k + 1)²

⇔ 4k² + 4k < 4k² + 4k + 1 (luôn đúng) do đó (3) luôn đúng với mọi số nguyên dương k.

Vậy (1) đúng khi n = k+ 1. Do đó theo nguyên lí quy nạp, (1) đúng với mọi số nguyên dương n.

Câu 4: Chứng minh với mọi số nguyên dương n ta có:

Hiển thị đáp án

*Với n = 1: Vế trái của

, vế phải của

Suy ra (1) đúng với n = 1.

*Giả sử (1) đúng với n = k. Có nghĩa là ta có:

Ta phải chứng minh (1) đúng với n= k+ 1. Có nghĩa ta phải chứng minh:

Thật vậy:

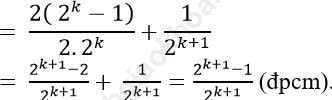
Vậy (1) đúng khi n = k+ 1. Do đó theo nguyên lí quy nạp, (1) đúng với mọi số nguyên dương n.

Câu 4: Chứng minh với mọi số nguyên dương n ta có:

Hiển thị đáp án

* Với n = 1: Vế trái của

, vế phải của

.

Suy ra (1) đúng với n = 1.

* Giả sử (1) đúng với k; k ∈ N*. Có nghĩa là ta có:

Ta phải chứng minh (1) đúng với n = k+ 1. Ta phải chứng minh:

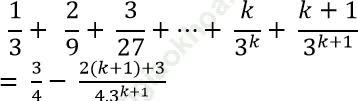
* Thật vậy:

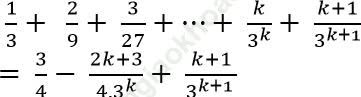
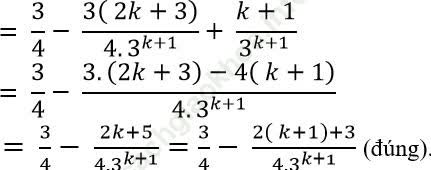
Vậy (1) đúng khi n= k+ 1. Do đó theo nguyên lí quy nạp, (1) đúng với mọi số nguyên dương n.

Câu 5: Chứng minh với mọi số nguyên n thì n³ + 11n chia hết cho 6.

Hiển thị đáp án

+ Với n = 1 ta có 1³ + 11.1 = 12 chia hết cho 6 đúng.

+Giả sử với n = k (k ∈ N*) thì k³ + 11k chia hết cho 6.

Ta phải chứng minh với n = k + 1 thì (k+1)³ + 11 (k+1) chia hết cho 6.

+ Thật vậy ta có:

(k+1)³ + 11 (k + 1) = k³ + 3k² + 3k + 1+ 11k + 11 = (k³ + 11k) + 3k (k + 1)+ 12 (*)

+ Do k³ + 11k chia hết cho 6 theo bước 2.

k (k + 1)⋮ nên 3k (k+1) ⋮ 6

và 12 ⋮ 6

=> (k³ + 11k) + 3k (k + 1) + 12 ⋮ 6

Từ đó suy ra (k + 1)³ + 11 (k + 1) ⋮ 6 (đpcm).

Câu 6: Chứng minh với mọi số nguyên dương n ta có: n³ + 3n² + 5n chia hết cho 3.

Hiển thị đáp án

* Đặt u_n = n³ + 3n² + 5n

* Ta có u₁ = 1³ + 3.1² + 5.1 = 9 ⋮ 3.

=> đúng với n = 1

* Giả sử u_k = k³ + 3k² + 5k ⋮ 3.

Ta cần chứng minh u_k+1 = (k+1)³ + 3. (k+1)² + 5 (k + 1) ⋮ 3

* Thật vậy, u_{k + 1} = k³ + 3k² +3k + 1 + 3k² + 6k + 3+ 5k + 5

⇔ u_k+1 = (k³ + 3k² + 5k) + (3k² + 9k + 9) = u_k + 3 (k² + 3k + 3)

Vì u_k ⋮ 3 và 3 (k² + 3k + 3) ⋮ 3 nên u_k+1 ⋮ 3

Vậy với mọi số nguyên dương n thì u_n chia hết cho 3.

Câu 7: Chứng minh với mọi số nguyên dương n ta có: 4ⁿ + 15n − 1 chia hết cho 9

Hiển thị đáp án

*Đặt u_n = 4ⁿ + 15n − 1

*Với n = 1, ta có u₁ = 4¹ + 15.1 − 1 = 18 chia hết cho 9

=> đúng với n = 1.

* Giả sử u_k = 4^k +15k − 1 chia hết cho 9.

Ta cần chứng minh u_{k + 1} = 4^{k + 1} + 15 (k + 1) − 1 chia hết cho 9.

*Thật vậy ta có: u_k+1 = 4.4^k + 15k+ 14 = 4 (4^k + 15k − 1) − 45k + 18 = 4. u_k + 9 (2 − 5k)

Vì 4u_k và 9 (2 − 5k) đều chia hết cho 9, nên u_k+1 cũng chia hết cho 9.

Vậy với mọi số nguyên dương n thì u_n chia hết cho 9.

Câu 8: Chứng minh với mọi số nguyên dương n thì 4ⁿ + 6n + 8 chia hết cho 9

Hiển thị đáp án

* Đặt u_n = 4ⁿ + 6n+ 8

* Với n = 1, ta có u₁ = 4¹ + 6.1 + 8 = 18 chia hết cho 9

=> đúng với n = 1.

* Giả sử u_k = 4^k + 6k + 8 chia hết cho 9.

Ta cần chứng minh u_{k + 1} = 4^{k + 1} + 6 (k+ 1)+ 8 chia hết cho 9.

Thật vậy ta có u_k+1 = 4.4^k + 6k + 14 = 4. (4^k + 6k + 8) − 18k + 18 = 4. u_k + 18 (1 − k)

Vì 4u_k và 18 (1 − k) đều chia hết cho 9, nên u_k+1 cũng chia hết cho 9.

Vậy với mọi số nguyên dương n thì u_n chia hết cho 9

Câu 9: Chứng minh với mọi số nguyên dương n ta có: 7.2^{2n − 2} + 3^{2n − 1} chia hết cho 5?

Hiển thị đáp án

* Đặt u_n = 7.2^{2n − 2} +3^{2n − 1}

* Với n = 1, ta có u₁ = 7.2^{2.1 − 2} + 3^{2.1 − 1} = 10 chia hết cho 5

=> đúng với n= 1.

* Giả sử u_k = 7.2^{2k − 2} +3^{2k − 1} chia hết cho 5.

Ta cần chứng minh u_k+1 = 7.2^2k + 3^{2k + 1} chia hết cho 5.

Thật vậy ta có u_k+1 = 4. (7.2^{2k− 2} + 3^{2k − 1}) − 4.3^{2k − 1} + 3^2k+1 = 4u_k + 5.3^{2k− 1}

Vì 4. u_k và 5.3^{2k− 1} đều chia hết cho 5, nên u_k+1 cũng chia hết cho 5.

Vậy với mọi số nguyên dương n thì un chia hết cho 5.

Câu 10: Chứng minh với mọi n nguyên và n ≥ 4 ta có: 3^{n − 1} > n (n+ 2) (1)

Hiển thị đáp án

* Với n = 4, VT = 3^{4 − 1} = 27 và VP = 4. (4 + 2)= 24

=> 27 > 24 nên (1) đúng với n = 4

* Giả sử với k ≥ 4; k ∈ N ta có: 3^{k− 1} > k (k+2).

Ta cần chứng minh: 3^k > (k + 1)(k + 3)

Thật vậy, ta có: 3^k = 3.3^{k− 1} > 3k. (k+ 2).

Lại có:

3k (k+ 2) > (k+1)(k+ 3) ⇔ 2k² +2k − 4 > 0 bất đẳng thức này đúng với mọi k ≥ k.

Suy ra 3^k > (k + 1)(k+3) (đúng).

Do đó theo nguyên lí quy nạp, (*) đúng với mọi số nguyên dương n ≥ 4.

Câu 11: Chứng minh với mọi số nguyên n và n ≥ 2 ta có:

Hiển thị đáp án

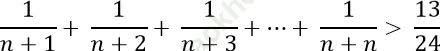
* Đặt

* Với n= 2 ta có

=> đúng với n= 2.

*Giả sử với n = k ≥ 2; k ∈ N thì (*) đúng, có nghĩa ta có:

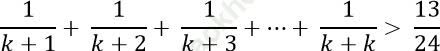
*Ta phải chứng minh (*) đúng với n=k+ 1, có nghĩa ta phải chứng minh:

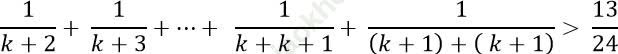
*Thật vậy ta có:

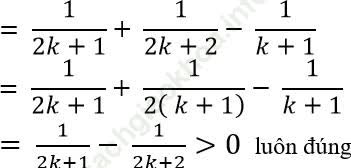
*Vậy u_k+1 > u_k >

(đúng). Vậy (*) đúng với n = k + 1.

*Suy ra (*) đúng với mọi số nguyên dương n ≥ 2.

Câu 12: Chứng minh với mọi số nguyên dương n ta có: nⁿ ≥ (n+1)^{n − 1} (1)

Hiển thị đáp án

* Với n = 1 ta có 1¹ ≥ (1+1)⁰ hay 1 ≥ 1 (đúng).

Vậy (1) đúng với n = 1.

* Giả sử với n = k; k ∈ N* thì (1) đúng, có nghĩa ta có: k^k ≥ (k+1)^{k − 1} (2).

Ta phải chứng minh (1) đúng với n= k+ 1, có nghĩa ta phải chứng minh:

(k+1)^k+1 ≥ (k+2)^k

Thật vậy, nhân hai vế của (2) với (k+1)^k+1 ta được:

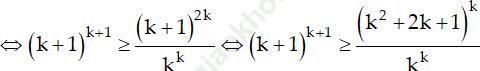
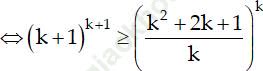
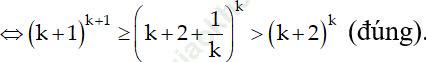
Vậy (*) đúng với n = k + 1. Do đó (*) đúng với mọi số nguyên dương n.

Bài tiếp: Dạng 2: Xác định số hạng của dãy số - Chuyên đề Toán 11