Phương trình lượng giác không mẫu mực - Chuyên đề Toán 11

A. Phương pháp giải

Để giải các phương trình lượng giác không mẫu mực ta cần sử dụng:

• Các công thức lượng giác: Công thức cộng; công thức nhân đôi; công thức biến đổi tích thành tổng; tổng thành tích...

• Sử dụng các hằng đẳng thức đáng nhớ...

• Đánh giá: a2 ≥ 0; vế trái ≤ a; vế phải ≥ a. Từ đó; suy ra: Vế trái = vế phải= a.

• Đánh giá: Vế trái > a; vế phải < 0 nên phương trình vô nghiệm.....

B. Ví dụ minh họa

Ví dụ 1. Giải phương trình:

A.

B.

C.

D. Cả A và C đúng

Bài giải:

Ví dụ 2. Giải phương trình:

A.

B.

C.

D. Đáp án khác

Bài giải:

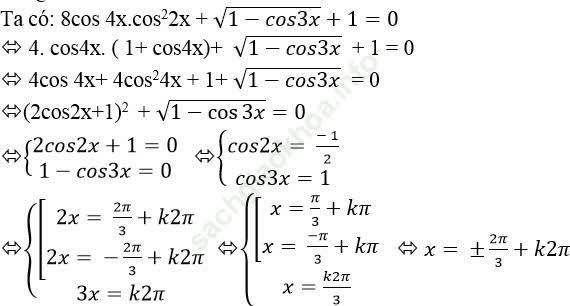
Ví dụ 3. Giải phương trình:

A.

B.

C. x = kπ

D.

Bài giải:

Đáp án đúng là: D.

Hướng dẫn:

Ta có: sin4x- cos4x = 1+ 4√ 2 sin⁡ (x- π/4)

⇒ sin 4x – (1+ cos4x) = 4 (sinx – cosx)

⇒ 2. sin2x. cos2 x- 2cos²2x = 4 (sinx- cosx)

⇒ 2cos 2x. ( sin2x – cos 2x) – 4 (sinx- cosx)= 0

⇒ 2 (cos² x- sin² x). (sin2x- cos2x) – 4. (sinx- cosx) = 0

⇒ 2. ( cosx- sinx). (cosx+ sinx). (sin2x- cos2x) + 4 (cosx + sinx) = 0

⇒ 2. ( cosx – sinx). [(cosx+ sinx) (sin2x- cos2x) + 2] = 0

Ví dụ 4. Giải phương trình sin3x. ( cosx - 2sin3x) + cos 3x. (1+ sinx - 2cos 3x) = 0

A. π/8 + kπ/2

B. k2π/3

C. kπ/4

D. Vô nghiệm

Bài giải:

Đáp án đúng là: D

Hướng dẫn

Ta có:

sin3x. ( cosx - 2sin3x) + cos 3x. (1 + sinx - 2cos 3x) = 0

⇒ sin3x. cosx – 2sin²3x + cos 3x + cos3x. sinx – 2cos²3x = 0

⇒ (sin3x. cosx + cos3x. sinx) – 2 (sin² 3x + cos² 3x) + cos3x = 0

⇒ sin4x –2 + cos3x = 0

⇒ sin4x + cos3x = 2 (*)

Với mọi x ta có: - 1 ≤ sin4x ≤ 1 và-1 ≤ cos3x ≤ 1

⇒ - 2 ≤ sin4x + cos3x ≤ 2

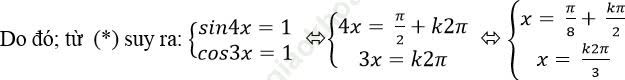
⇒ Không có giá trị nào của x thỏa mãn.

Vậy phương trình đã cho vô nghiệm

Ví dụ 5. Giải phương trình:

A.

B.

C.

D. Vô nghiệm

Bài giải:

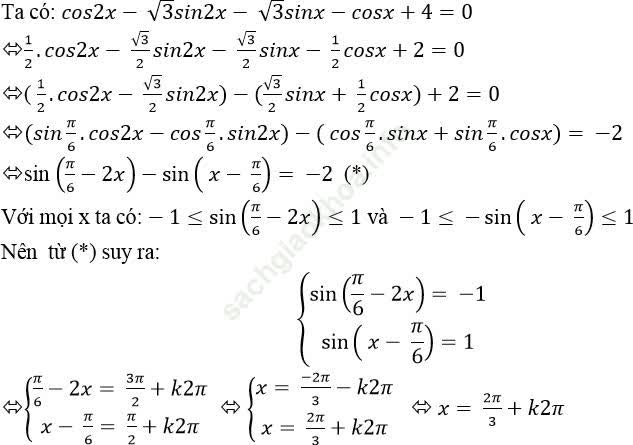
Ví dụ 6. Giải phương trình sin²⁰x + cos²⁰ x = 1

A. x = kπ

B. x = kπ/2

C. x = π/2 + kπ

D. x = kπ/4

Bài giải:

Đáp án đúng là: B.

Hướng dẫn:

Ta có: sin²⁰ x + cos²⁰ x = 1

⇒ sin²⁰ x + cos²⁰ x = sin² x + cos² x

⇒ sin²⁰ x - sin² x = cos² x - cos²⁰ x

⇒ sin² x (sin¹⁸ x – 1) = cos² x (1 - cos¹⁸ x)

+ Với mọi x ta luôn có: - 1 ≤ sinx ≤ 1 ⇒ 0 ≤ sin² x ≤ 1

⇒ sin¹⁸x - 1 < 0

⇒ vế trái ≤ 0 (1)

+ Tương tự có: 1 - cos¹⁸x ≥ 0

⇒ Vế phải ≥ 0 (2)

Từ (1) và (2) suy ra: Vế trái = Vế phải = 0

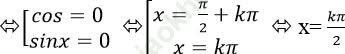
Vậy nghiệm phương trình đã cho là x= kπ/2

Ví dụ 7. Giải phương trình:

A. x = π/4 + kπ

B. kπ

C. Vô nghiệm

D. Cả A và B đúng

Bài giải:

Ví dụ 8. Giải phương trình:

A.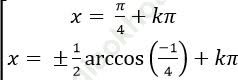

B.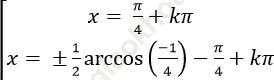

C.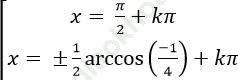

D. Phương trình vô nghiệm

Bài giải:

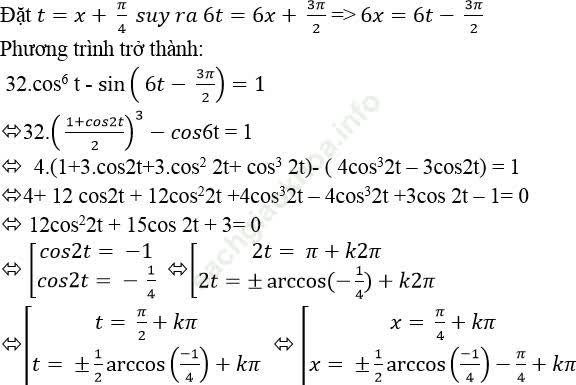
Ví dụ 9. Giải phương trình:

A.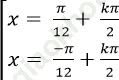

B.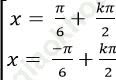

C.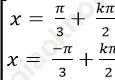

D. Đáp án khác

Bài giải:

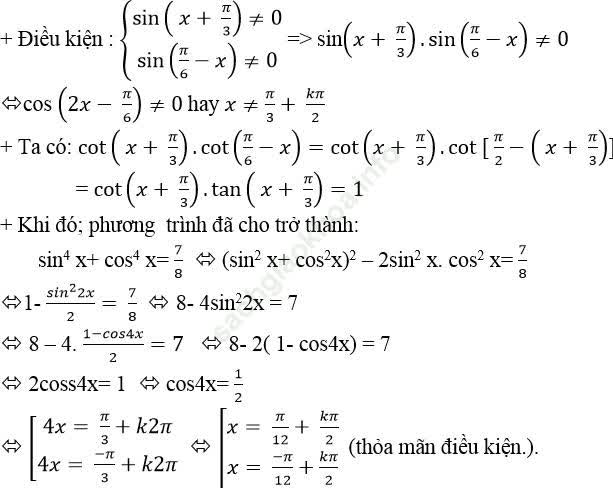
Ví dụ 10. Giải phương trình:

A.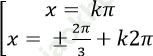

B.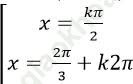

C.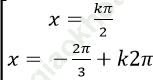

D.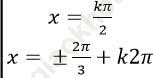

Bài giải:

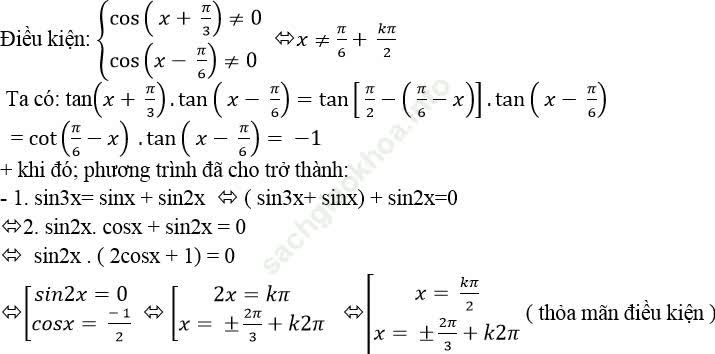
Ví dụ 11. Cho phương trình:

Nghiệm dương nhỏ nhất của phương trình có dạng πa/b với a; b là các số nguyên và nguyên tố cùng nhau. Tính S = b - a

A. 2

B. 3

C. 4

D. 1

Bài giải:

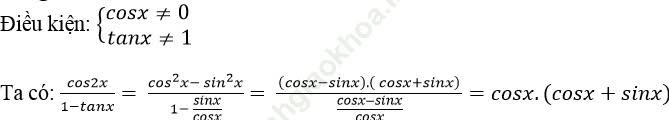
=> phương trình đã cho trở thành:

2²⁰¹⁷. (sin²⁰¹⁸x + cos²⁰¹⁸x). (sinx + cosx). cosx = cosx (sinx + cosx)

⇒ 2²⁰¹⁷. (sin²⁰¹⁸x + cos²⁰¹⁸x). (sinx + cosx). cosx - cosx (sinx + cosx) = 0

⇒ cosx. ( cosx+ sinx). [2²⁰¹⁷. (sin²⁰¹⁸x + cos²⁰¹⁸x) - 1] = 0

Ví dụ 12. Giải phương trình:

A.

B.

C.

D.

Bài giải:

Đáp án đúng là: A.

Hướng dẫn

+ Điều kiện: sinx ≠ 0

Ví dụ 13. Giải phương trình: sin3x. ( cosx- 2sin3x) + cos3x. (1+ sinx – 2cos3x) =0

A.

B.

C.

D. Vô nghiệm

Bài giải:

Đáp án đúng là: D.

Hướng dẫn:

Ta có: sin3x. ( cosx- 2sin3x) + cos3x. (1+ sinx – 2cos3x) = 0

⇒ sin3x. cosx – 2sin²3x + cos3x + cos3x. sinx – 2cos²3x=0

⇒ (sin3x. cosx + cos3x. sinx) - 2 (sin²3x + cos²3x) +cos3x = 0

⇒ sin4x - 2+ cos3x= 0

⇒ sin4x + cos3x = 2 (1)

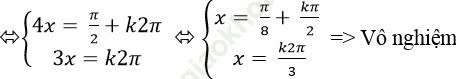
Vậy phương trình đã cho vô nghiệm.

C. Bài tập vận dụng

Câu 1: Giải phương trình:

A.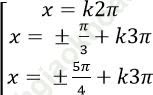

B.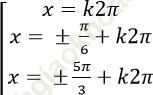

C.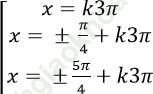

D. Đáp án khác

Hiển thị lời giải

Chọn C.

Câu 2:Giải phương trình:

A.

B.

C.

D.

Hiển thị lời giải

Chọn D.

Câu 3: Giải phương trình:

A.

B.

C.

D.

Hiển thị lời giải

Chọn C.

Câu 4: Giải phương trình:

A.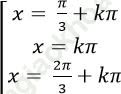

B.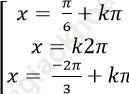

C.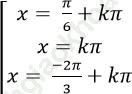

D.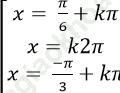

Hiển thị lời giải

Chọn C.

Câu 5: Giải phương trình:

A.

B.

C.

D.

Hiển thị lời giải

Chọn D.

Câu 6: Giải phương trình:

A.

B.

C.

D. Vô nghiệm

Hiển thị lời giải

Vậy hệ phương trình đã cho vô nghiệm

Chọn D.

Câu 6:Giải phương trình

A.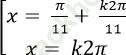

B.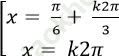

C.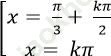

D.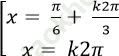

Hiển thị lời giải

+ Ta thấy khi sinx=0 ⇒ x= kπ không phải là nghiệm của phương trình.

+ Nhân hai vế của phương trình (*) với sinx ≠ 0 ta được:

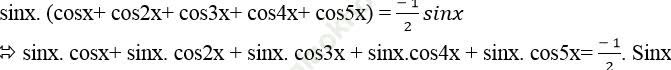
⇒ 2sinx. cosx+ 2sinx. cos2x+ 2sinx. cos3x + 2sinx. cos4x + 2sinx. cos5x + sinx=0

⇒ sin2x – sinx + sin3x- sin2x + sin4x- sin3x + sin5x- sin4x+ sin6x + sinx= 0

⇒ sin 5x+ sin 6x = 0

⇒ sin5x= - sin6x= sin (π-6x)

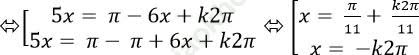
Chọn A.

Câu 7: Giải phương trình: 4sin3x. cos2x =1+ 6sinx – 8sin³ x

A.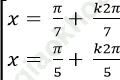

B.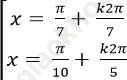

C.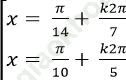

D.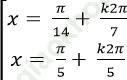

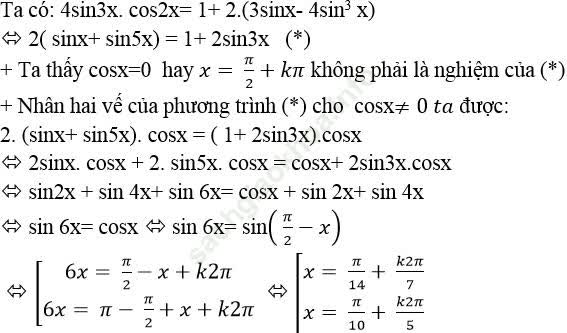
Hiển thị lời giải

Chọn C.

Câu 8:Giải phương trình: cosx. cos2x. cos4x. cos 8x= 1/16 (*)

A.

B.

C.

D. Đáp án khác

Hiển thị lời giải

+ Ta thấy khi sinx=0 hay x=kπ không phải là nghiệm của phương trình đã cho.

+ Nhân hai vế của phương trình (*) với sin x ≠ 0 ta được:

Chọn D.

Câu 9:Nghiệm dương nhỏ nhất của phương trình cos3x. (2cos2x+ 1) = 1/2 có dạng πa/b với a; b là các số nguyên và nguyên tố cùng nhau. Tính S= a. b

A. 6

B. 7

C. 8

D. 9

Hiển thị lời giải

Ta có: cos3x. (2cos2x+ 1) = 1/2

⇒ 4. cos3x. cos2x+ 2cos3x= 1

⇒ 2. ( cos5x+ cosx) + 2cos3x= 1

⇒ 2cos5x+ 2cosx+ 2cos3x=1

+ Nhận thấy sinx=0 hay x=kπ không thỏa mãn phương trình trên.

+ Nhân hai vế cho sinx ≠ 0 ta được:

2. sinx. cos5x+ 2. cosx. sinx + 2cos3x. sinx= sinx

⇒ sin6x + sin (-4x) + sin2x + sin 4x + sin (- 2x) = sinx

⇒ sin6x - sin 4x + sin2x+sin4x – sin2x- sinx=0

⇒ sin6x- sinx=0 ⇒ sin6x= sinx

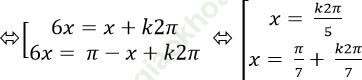
Suy ra nghiệm dương nhỏ nhất là π/7 ⇒ a= 1 và b= 7

⇒ S= a. b= 1.7= 7

Chọn B.

Câu 10: Cho phương trình sin²⁰¹⁸x + cos²⁰¹⁸x = 2 (sin²⁰²⁰x+ cos²⁰²⁰x). Số vị trí biểu diễn các nghiệm của phương trình trên đường tròn lượng giác là

A. 3

B. 4

C. 6

D. 8

Hiển thị lời giải

Ta có: sin²⁰¹⁸x+ cos²⁰¹⁸ x= 2 (sin²⁰²⁰x+ cos²⁰²⁰x)

⇒ (sin²⁰¹⁸ x- 2sin²⁰²⁰ x) + (cos²⁰¹⁸ x- 2cos²⁰²⁰ x) = 0

⇒ sin²⁰¹⁸ x. (1 – 2sin² x) + cos²⁰¹⁸x. ( 1- 2cos² x) = 0

⇒ sin²⁰¹⁸ x. cos2x – cos²⁰¹⁸x. cos2x= 0

⇒ cos2x. ( sin²⁰¹⁸ x- cos²⁰¹⁸x)= 0

Chọn B.

Câu 11: Nghiệm dương lớn nhất của phương trình tan²⁰¹⁸ x+ cot²⁰¹⁸x = 2. sin²⁰¹⁷(x+ π/4) có dạng πa/b với a; b là các số nguyên a > 0 và a; b nguyên tố cùng nhau. Tính S= a. b

A. 4

B. 3

C. 6

D. 8

Hiển thị lời giải

⇒ nghiệm dương lớn nhất là x= π/4

⇒ a= 1 và b= 4 nên S=a. b = 4

Chọn A.

Câu 12: Giải phương trình:

A. x = kπ/4

B. x = kπ/2

C. kπ

D. kπ/3

Hiển thị lời giải

+ Ta có: 4cos²2x + sin²2x = (cos² 2x + sin²2x) +3cos²2x

= 1+ 3cos²2x > 0 với mọi x.

⇒ Phương trình luôn xác định với mọi giá trị của x.

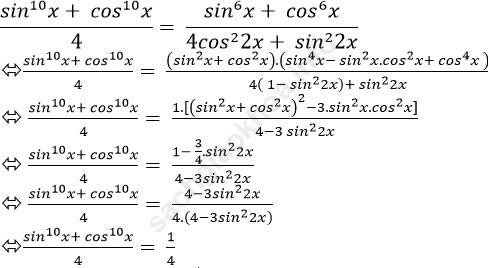
⇒ sin¹⁰x + cos¹⁰x = 1

⇒ sin¹⁰ x+ cos¹⁰ x= sin² x+ cos² x

⇒ (sin¹⁰ x- sin² x)+ (cos10x – cos² x) = 0

⇒ sin² x (sin⁸x -1) + cos² x (cos⁸ x- 1) = 0 (*)

Với mọi ta có: - 1 ≤ sinx; cosx ≤ 1

⇒ sin⁸ x- 1 < 0 và cos⁸ x – 1 < 0 nên từ (*) suy ra:

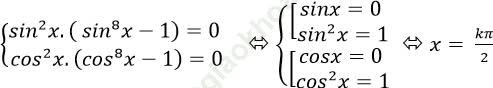
Chọn B.

Câu 13: Cho phương trình: 4cos²x+ tan² x+ 4= 2. (2cosx – tanx). Tìm số nghiệm của phương trình trên khoảng (0; 10π)?

A. 10

B. 16

C. 22

D. Vô nghiệm

Hiển thị lời giải

Điều kiện: cosx ≠ 0 hay x ≠ π/2+kπ

Ta có: 4cos² x+ tan² x+ 4= 2. ( 2cosx- tanx)

⇒ 4cos² x – 4cosx + 1+ tan²x + 2tanx + 1+ 2= 0

⇒ (2cosx-1)² + (tanx+ 1)² + 2= 0

Với mọi x thỏa mãn điều kiện ta có: (2cosx -1)² ≥ 0 và (tanx+ 1)² ≥ 0

⇒ (2cosx-1)² + (tanx+ 1)² + 2 > 0

⇒ Phương trình đã cho vô nghiệm.

Chọn D.

Bài trước: Phương trình lượng giác đưa về dạng tích - Chuyên đề Toán 11 Bài tiếp: Tìm số nghiệm của phương trình lượng giác trong khoảng, đoạn - Chuyên đề Toán 11