Cách tìm số hạng thứ n của dãy số cực hay có lời giải - Chuyên đề Toán 11

A. Phương pháp giải

Cho dãy số bởi công thức của số hạng tổng quát: u_n = f (n). Khi đó số hạng đứng thứ k của dãy số là: u_k = f (k).

B. Ví dụ minh họa

Ví dụ 1: Cho dãy số (u_n) với u_n = 2n + 1. Mệnh đề nào sau đây là sai?

A. u₃ là số nguyên tố.

B. u₅ không chia hết cho 5

C. u₇ = 15

D. u₈ = 18

Bài giải:

Ta xét các phương án:

+ Ta có: u₃ = 2.3 + 1 = 7 là số nguyên tố => A đúng

+ u₅ = 2.5 + 1 = 11 là số không chia hết cho 5. => B đúng

+ u₇ = 2.7 + 1 = 15 => C đúng.

+ u₈ = 2.8 + 1 = 17 => D sai

Vậy phương án sai là: D.

Ví dụ 2: Cho dãy số (u_n) với . Khẳng định nào sau đây là đúng?

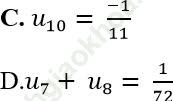
Bài giải:

Ta xét các phương án, cụ thể như sau:

+ Ba số hạng đầu tiên của dãy số là: => A sai.

+ Tổng hai số hạng đầu tiến là: => B đúng

+ Số hạng thứ 10 là: => C sai.

+ Ta có:

=> Khẳng định đúng là: B.

Ví dụ 3: Cho dãy số (u_n) được xác định bởi u₁ = 1 và với mọi n ≥ 2. Tìm số hạng thứ 4 của dãy số.

Bài giải:

Ta có:

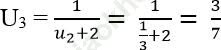
Và:

Đáp án đúng là: A.

Ví dụ 4: Cho dãy số (u_n) xác định bởi: u₁ = 1; u₂ = 2 và u_n = u_{n− 1} + u_{n− 2}. Số hạng thứ 5 của dãy số là:

A. 6

B. 7

C. 8

D. 9

Bài giải:

Ta có; u₃ = u₁ + u₂ = 1 + 2 = 3

u₄ = u₂ + u₃ = 2 + 3 = 5

Và u₅ = u₃ + u₄ = 3 + 5 = 8

Đáp án đúng là: C.

Ví dụ 5: Cho dãy số (u_n) xác định bởi . Số hạng thứ 4 của dãy số là:

Bài giải:

Ta có:

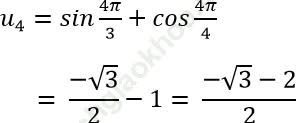
Đáp án đúng là: B.

Ví dụ 6: Cho dãy số (u_n) biết u_n = n² + n − √ n. Tính u₉ − u₄?

A. 75

B. 65

C. 69

D. 71

Bài giải:

+ Ta có: u₉ = 9² + 9 − √ 9 = 87.

Và u₄ = 4² + 4 − √ 4 = 18

=> u₉ − u₄ = 87 − 18 = 69

Đáp án đúng là: C

Ví dụ 7: Cho dãy số (u_n) với (a: hằng số). u_n+1 là số hạng nào sau đây?

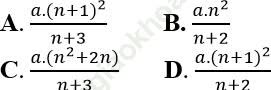
Bài giải:

Ta có:

Đáp án đúng là: A.

Ví dụ 8: Cho dãy số (u_n) với (a: hằng số). Khẳng định nào sau đây là sai?

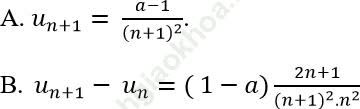
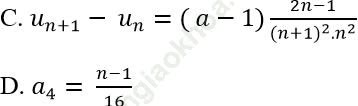
Bài giải:

Ta có:

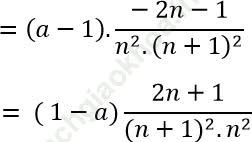
Và

=> C sai

Vậy khẳng định C là sai.

Ví dụ 8: Cho dãy số (u_n) được xác định bởi

Bài giải:

Ta có;

=> Số hạng thứ 100 của dãy số là:

Đáp án đúng là: D.

C. Bài tập trắc nghiệm

Câu 1: Cho dãy số (u_n) được xác định bởi 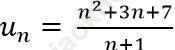. Viết năm số hạng đầu của dãy;

Hiển thị đáp án

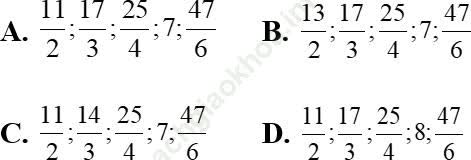
Đáp án: A

Ta có năm số hạng đầu của dãy

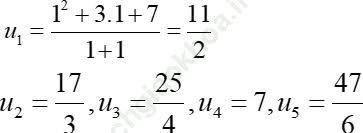
Câu 2: Cho dãy số (u_n) được xác định bởi: 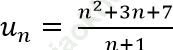. Hỏi dãy số có bao nhiêu số hạng nhận giá trị nguyên.

A. 2 B. 4 C. 1 D. 0

Hiển thị đáp án

Đáp án: C

Ta có:

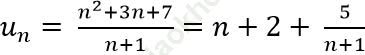
Do đó u_n nguyên khi và chỉ khi nguyên hay (n + 1) ∈ Ư (5).

Kết hợp với n nguyên dương suy ra: n + 1= 5

⇔ n= 4

Vậy dãy số có duy nhất một số hạng nguyên là u₄ = 7.

Câu 3: Cho dãy số (u_n) xác định bởi: 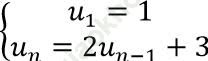. Viết năm số hạng đầu của dãy

A. 1; 5; 13; 28; 61

B. 1; 5; 13; 29; 61

C. 1; 5; 17; 29; 61

D. 1; 5; 14; 29; 61

Hiển thị đáp án

Đáp án: B

Ta có 5 số hạng đầu của dãy là:

u₁ = 1; u₂ = 2u₁ + 3 = 5; u₃ = 2u₂ + 3 = 13

u₄ = 2u₃ + 3 = 29 và u₅ = 2u₄ + 3 = 61

Câu 4: Cho dãy số (u_n) xác định bởi

. Tính u₄₈?

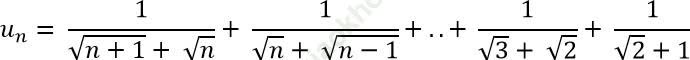
A. 6 B. 7 C. 8 D. 5

Hiển thị đáp án

Đáp án: A

Ta có

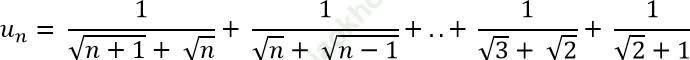
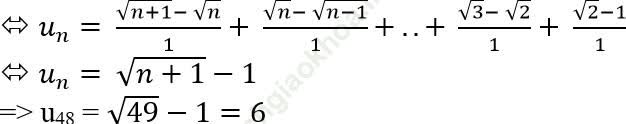
Câu 5: Cho dãy số (u_n) được xác định bởi u₁ = 3 và u_n+1 = u_n + 10. Xác định số hạng thứ 50 của dãy số này?

A. 465 B. 378 C. 493 D. 452

Hiển thị đáp án

Đáp án: C

*Ta có: u₂ = 13; u₃ = 23; u₄ = 33.

=> Dự đoán: số hạng thứ n của dãy số là u_n = 3 + 10 (n − 1).

* Thật vậy; ta chứng minh bằng phương pháp quy nạp

+ với n = 1 ta có u₁ = 3 đúng

+ Giả sử đúng với n = k; tức là u_k = 3 + 10 (k − 1).

Ta chứng minh đúng với n = k + 1 tức là đi chứng minh: u_k+1 = 3 + 10k.

Ta có: u_k+1 = u_k + 10 = 3 + 10 (k − 1) + 10 = 3 + 10k

=> điều phải chứng minh.

=> Số hạng thứ 50 của dãy số là: u₅₀ = 3 + 10 (50 − 1) = 493.

Câu 6: Cho dãy số (u_n) được xác định bởi u₁ = 2 và u_n+1 = u_n. 5. Xác định số hạng thứ 30 của dãy số.

A. 2.5¹⁵ B. 2.5²⁹ C. 2.5³⁰ D. 2.5²⁰

Hiển thị đáp án

Đáp án: B

*Ta có: u₂ = 10; u₃ = 50, u₄ = 250....

Dự đoán: u_n = 2.5^{n − 1}

* Ta dùng quy nạp chứng minh u_n = 2.5^{n − 1}

+ Với n = 1 ta có: u₁ = 2.5⁰ = 2 (đúng với n = 1).

+ Giả sử đúng với n = k, tức là; u_k = 2.5^{k − 1}

Ta chứng minh đúng với n = k + 1. Tức là ta chứng minh u_k+1 = 2.5^k

Theo giả thiết ta có: u_k+1 = 5. u_k = 5.2.5^{k− 1} = 2.5^k

=> đúng với n = k + 1 => điều phải chứng minh.

* số hạng thứ 30 của dãy số là: u₃₀ = 2.5²⁹

Câu 7: Cho dãy số (u_n) xác định bởi u₁ = 2 và u_n+1 = √ (2 + u_n). Tìm số hạng thứ 1000 của dãy số đó?

A. 2 B. √ 8 C. √ 1000 D. √ 320

Hiển thị đáp án

Đáp án: A

* Ta có: u₂ = 2; u₃ = 2; u₄ = 2..

Dự đoán: u_n = 2 với mọi n.

* Ta dùng quy nạp để chứng minh u_n = 2.

+ ta có: u₁ = 2 nên đúng với n = 1.

+ Giả sử đúng với mọi số nguyên n = k. Tức là: u_k =2.

Ta chứng minh đúng với n = k + 1. Tức là ta đi chứng minh; u_k+1 = 2.

Thật vậy ta có: u_k+1 = √ (2+ u_k)= √ (2+2) = 2

=> đúng với n= k + 1 (đpcm)

* Vậy u_n = 2 với mọi n nên u₁₀₀₀ = 2.

Câu 8: Cho dãy số (u_n) xác định bởi . Tìm số hạng thứ 4 của dãy số?

Hiển thị đáp án

Đáp án: A

Ta có số hạng đầu tiên của dãy số là:

Câu 9: Cho dãy số (un) xác đinh bởi:

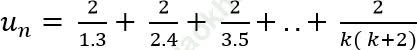. Tính số hạng thứ 50 của dãy số.

Hiển thị đáp án

Đáp án: C

Ta có:

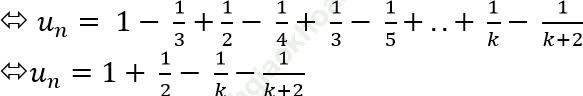
=> Số hạng thứ 50 của dãy số là:

Bài tiếp: Cách tìm công thức của số hạng tổng quát cực hay có lời giải - Chuyên đề Toán 11