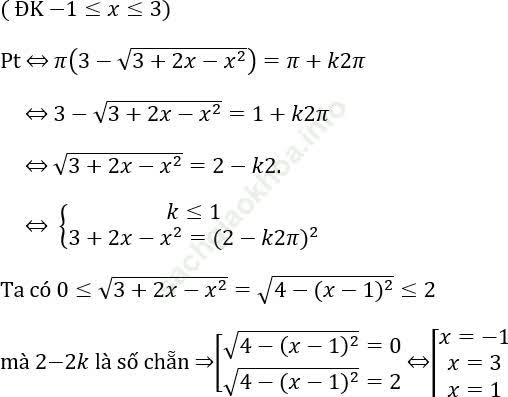Dạng 7: Tìm nghiệm của phương trình lượng giác thỏa mãn điều kiện - Chuyên đề Toán 11

Tìm nghiệm của phương trình lượng giác thỏa mãn điều kiện

A. Ví dụ

Bài 1: Tìm tổng các nghiệm của phương trình:

sin (3x + π /3) = cos (2x - π /4) trong khoảng (- π, π)

Bài giải:

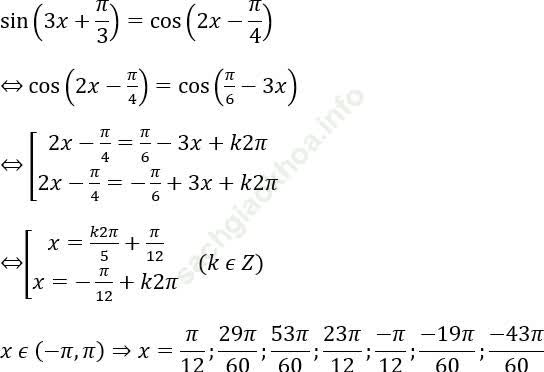
Vậy tổng các nghiệm là: 9π /4

Bài 2: Tìm nghiệm nguyên của phương trình:

Thử lại ta có các nghiệm nguyên: x = -7 (k = -2); x = -31 (k = 10)

B. Bài tập vận dụng

Bài 1: Tìm tổng các nghiệm của phương trình sin²2x = cos²(3x - π /8) trong khoảng (- π, π)

Bài giải:

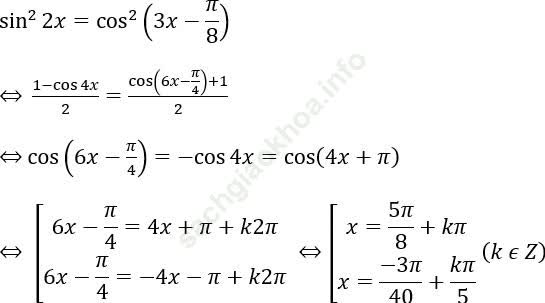
x ∈ (-π, π) ⇒ x = 5π /8; (-7π)/8; (-27π)/40; (-19π)/40; (-11π)/40; (-3π)/40; π /8; 13π /40; 21π /40; 29π /40; 37π /40

Tổng các nghiệm là: 7π /8

Bài 2: Tìm nghiệm dương nhỏ nhất của phương trình: sin²2x + cos²5x = 1.

Bài giải:

Bài 3: Tìm nghiệm âm lớn nhất của phương trình: (sinx + cosx)² = 2cos²3x.

Bài giải:

(sin⁡x + cos⁡x)² = 2 cos²⁡3x

⇔ 1 + sin 2x = cos⁡6x+1

⇔ sin⁡2x = cos⁡6x

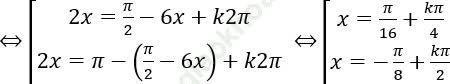
Vậy nghiệm dương nhỏ nhất là: (-π)/8

Bài 4: Tìm x ∈ [0,14] nghiệm đúng phương trình: cos3x – 4cos2x + 3cosx – 4 = 0.

Bài giải:

cos3x- 4 cos⁡2x + 3 cos⁡x - 4 = 0

⇔ 4 cos³x - 3 cos⁡x- 8 cos²⁡x + 4 + 3 cos⁡x - 4 = 0

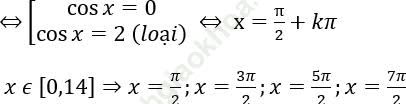
Bài 5: Tìm nghiệm nguyên dương của phương trình:

Bài giải: