Đoạn vuông góc chung của hai đường thẳng chéo nhau trong không gian (dùng quan hệ song song) - Chuyên đề Toán 11
A. Phương pháp giải
Để tính khoảng cách giữa hai đường thẳng chéo nhau ta có thể dùng một trong các cách sau:
* Cách 1:
Chọn mặt phẳng (α) chứa đường thẳng Δ và song song với Δ '. Khi đó d (Δ, Δ ') = d (Δ ', (α))
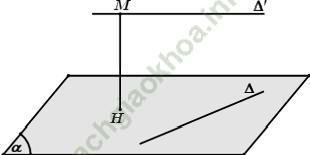
* Cách 2:
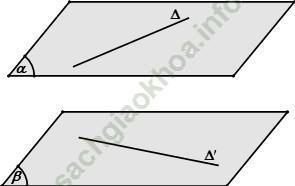
Dựng hai mặt phẳng song song và lần lượt chứa hai đường thẳng. Khoảng cách giữa hai mặt phẳng đó là khoảng cách cần tìm.
B. Ví dụ minh họa
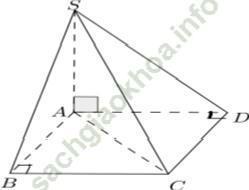
Ví dụ 1: Cho hình chóp S. ABCD có SA ⊥ (ABCD), đáy ABCD là hình chữ nhật với AC = a√ 5 và BC = a√ 2. Tính khoảng cách giữa SD và BC.

Bài giải:
Đáp án đúng là: D
Ta có: BC // AD (Tính chất hình chữ nhật) mà AD ⊂ (SAD)
⇒ BC // mặt phẳng (SAD)
d (BC, SD) = d (BC, (SAD)) = d (B, SAD)
Vậy d (SD; BC) = AB = a√ 3
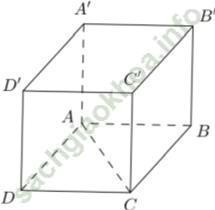
Ví dụ 2: Cho hình lập phương ABCD. A'B'C'D' có cạnh bằng a. Khoảng cách giữa BB’ và AC bằng:

Bài giải:
Đáp án đúng là: C.
+ Ta có: BB’ // CC’ mà CC’ ⊂ (ACC’A’) nên: BB’ // (ACC’A’)
⇒ d (BB’; AC) = d (BB’; (ACC’A’) = d (B; (ACC’A’)
+ Gọi O là giao điểm của AC và BD
⇒ BO ⊥ (ACC’A’) (tính chất hình lập phương)
Ví dụ 3: Cho hình chóp S. ABCD có đáy là hình thang vuông tại A và B; AB = BC = a và AD = 2a; SA vuông góc với mặt đáy và SA = a. Tính khoảng cách giữa SB và CD?
I
Bài giải:
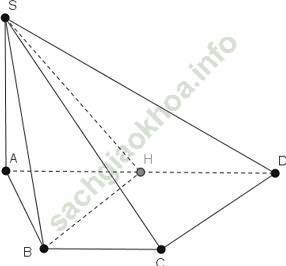
Gọi H là trung điểm AD => AH = HD = a
+ Tứ giác HDCB có HD // BC và HD = BC = a
⇒ HDCB là hình bình hành.
⇒ CD // HB nên CD // mặt phẳng (SHB)
+ Do H là trung điểm của AB và CD // (SHB) nên: d (CD; SB) = d (CD; (SBH))= d (D; (SBH)) = d (A; (SBH))
+ Tứ diện A. BHS có:
AB = AH = AS và AB; AH; SA đôi một vuông góc nên:
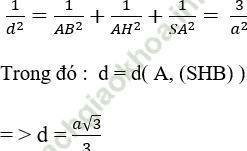
Vậy d (SB; CD) = d (A, (SHB)) = (a√ 3)/3
Đáp án đúng là: C
Ví dụ 4: Cho hình chóp S. ABCD có đáy là hình vuông cạnh a. Đường thẳng SA vuông góc với mặt phẳng đáy, SA = a. Khoảng cách giữa hai đường thẳng SB và CD nhận giá trị nào trong các giá trị sau?
A. a
B. a√ 2
C. a√ 3
D. 2a
Bài giải:
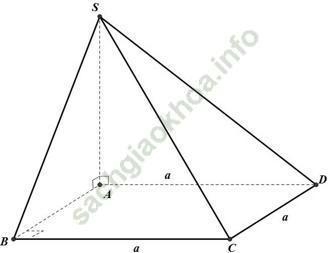
Ta có: CD // AB nên CD // (SAB)
⇒ d (CD; AB) = d (CD; (SAB)) = d (D; SAB)) = AD = a
(vì AD ⊥ AB và AD ⊥ SA nên AD ⊥ (SAB))
Đáp án đúng là: A
Ví dụ 5: Cho tứ diện OABC trong đó OA; OB; OC đôi một vuông góc với nhau và OA = OB = OC = a. Gọi I là trung điểm BC. Khoảng cách giữa AI và OC bằng bao nhiêu?

Bài giải:
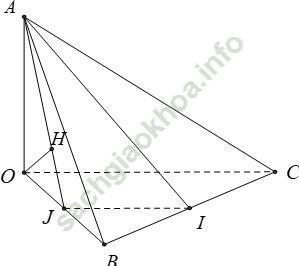
Gọi J là trung điểm OB. Kẻ OH vuông góc AJ tại H
+ Tam giác AOJ vuông tại O, có OH là đường cao
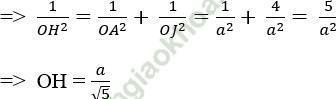
+ Do I và J lần lượt là trung điểm của BC và BO nên IJ là đường trung bình của ∆ ABC và IJ // OC
Mà IJ ⊂ (AIJ) nên OC // (AIJ).
+ Ta có 3 đường thẳng OA; OB; OC đôi một vuông góc nên OC ⊥ (OAB)
⇒ IJ ⊥ (OAB) và IJ ⊥ OH (1)
Lại có: AJ ⊥ OH (2)
Từ (1) và (2) => OH ⊥ (AIJ)
+ Khi đó: d (AI; OC) = d (OC; (AIJ)) = d (O; (AIJ)) = OH = a/√ 5
Đáp án đúng là: B
Ví dụ 6: Cho hình vuông ABCD và ∆ đều SAD nằm trong hai mặt phẳng vuông góc với nhau và AD = a. Tính khoảng cách giữa AD và SB.
Bài giải:
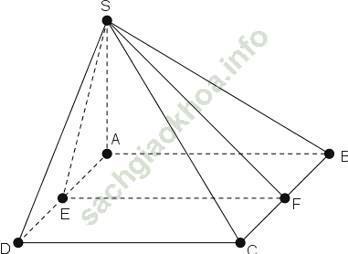
Gọi E, F lần lượt là trung điểm AD và B.
+ Tam giác SAD là ∆ đều nên SE ⊥ AD (1)
+ Lại có: Hai mặt phẳng (ABCD) và (SAD) cắt nhau theo giao tuyến AD và nằm trong hai mặt phẳng vuông góc với nhau (2).
Từ (1) và (2) => SE ⊥ (ABCD).
+ Gọi H là hình chiếu vuông góc của E lên SF. Ta chứng minh EH ⊥ (SBC).
Thật vậy, ta có: EH ⊥ SF (cách dựng) và EH ⊥ BC (do BC ⊥ (SEF)
⇒ EH ⊥ (SBC).
+ Do AD // BC; SB ⊂ (SBC) và EH ⊥ (SBC)
⇒ d (AD: SB) = d (AD; (SBC) = d (E; (SBC)) = EH
+ Xét ∆ vuông SEF có:
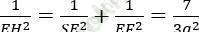
Trong đó: SE = a√ 3; EF = AB = a
⇒ EH = (a√ 21)/7
Đáp án đúng là: B
Ví dụ 7: Cho hình lập phương ABCD. A'B'C'D' có cạnh bằng a. Khoảng cách giữa BB’ và AC bằng:

Bài giải:
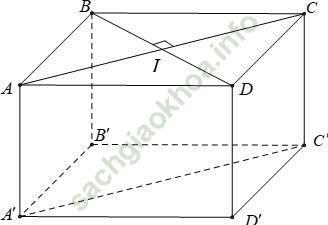
Gọi I là giao điểm của AC và BD.
+ Vì ABCD. A’B’C’D’ là hình lập phương nên BI ⊥ (AA'C'C).
+ Ta có: BD = BC√ 2 = a√ 2 nên IB = BD/2 = (a√ 2)/2
+ Khi đó: d (BB’; AC)= d (BB’; ( AA’C’C) = IB = (a√ 2)/2
Đáp án đúng là: C
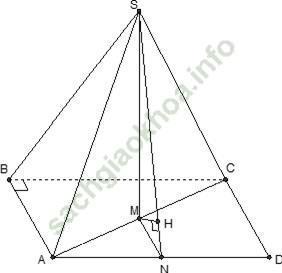
Ví dụ 8: Cho hình chóp S. ABC có đáy ABC là tam giác vuông tại B; AB = a cạnh bên SA vuông góc với đáy và SA = a√ 2. Gọi M là trung điểm của AB. Khoảng cách giữa SM và BC bằng bao nhiêu?

Bài giải:
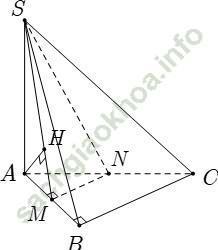
Gọi N là trung điểm của cạnh đáy AC.
+ Tam giác ABC có MN là đường trung bình nên MN // BC
⇒ BC // (SMN) mà SM ⊂ (SMN) nên:
d (SM; BC) = d (BC; (SMN)) = d (B; (SMN)) = d (A; (SMN))
Gọi H là hình chiếu vuông góc của A trên đoạn SM.
+ Ta chứng minh: MN ⊥ (SAM):

Đáp án đúng là: A
Ví dụ 9: Cho lăng trụ ∆ đều ABC. A1B1C1 có cạnh đáy bằng a, cạnh bên bằng b. Tính khoảng cách giữa AB và CC1
Bài giải:
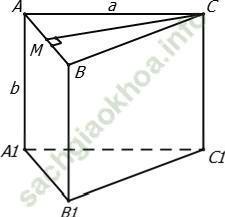
Gọi M là trung điểm của AB
+ Ta có: CC1 // AA1 mà AA1 ⊂ (ABB1A1)
⇒ CC1 // (ABB1A1)
⇒ d (CC1; AB) = d (CC1; (ABB1A1)) = d (C; ( ABB1A1))
+ Ta chứng minh CM ⊥ (ABB1A1):
- Do ∆ ABC đều nên CM là đường trung tuyến đồng thời là đường cao: CM ⊥ AB. (1)
- CM ⊥ AA1( tính chất lăng trụ tam giác đều) (2)
Mà AB và AA1 (ABB1A1), kết hợp với (1) và (2) suy ra:
CM ⊥ (ABB1A1)
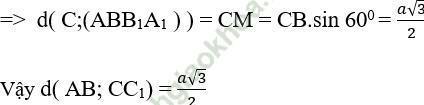
Đáp án đúng là: B
Ví dụ 10: Cho hình chóp S. ABCD có đáy là hình vuông cạnh a, SD = a√ 17/2. Hình chiếu vuông góc H của đỉnh S lên mặt phẳng (ABCD) là trung điểm của cạnh AB. Gọi K là trung điểm của AD. Tính khoảng cách giữa hai đường SD và HK theo a.

Bài giải:
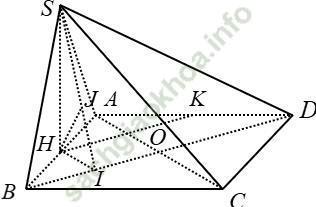
+ Ta có: H và K lần lượt là trung điểm của AB và AD nên HK là đường trung bình của ∆ ABD
⇒ HK // BD ⇒ HK // (SBD)
⇒ d (SD; HK) = d (HK; (SBD)) = d (H, (SBD))
Kẻ HI ⊥ BD và HJ ⊥ SI


Đáp án đúng là: C
Ví dụ 11: Cho hình chóp tứ giác S. ABCD có đáy ABCD là hình vuông tâm O, cạnh bằng 2a. Mặt bên SAB là tam giác đều, SI vuông góc với (SCD) và I là trung điểm AB. Khoảng cách giữa hai đường thẳng SO và AB là:

Bài giải:
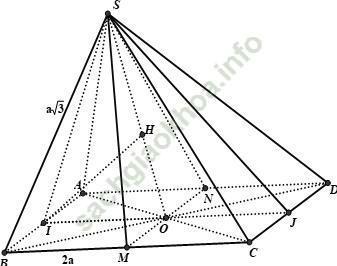
Kẻ MN // AB ⇒ AB // (SMN)
⇒ d (SO; AB) = d (AB; (SMN)) = d (I, (SMN))
Ta có: AB ⊥ SI ⇒ MN ⊥ SI, AB ⊥ OI ⇒ MN ⊥ OI
⇒ MN ⊥ (SOI) ⇒ (SMN) ⊥ (SOI).
Kẻ IH ⊥ SO ⇒ IH ⊥ (SMN)
⇒ IH = d (I, (SMN))
+ Gọi J là trung điểm của CD
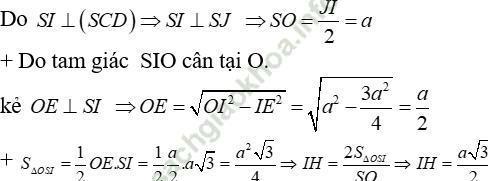
Đáp án đúng là: C
Ví dụ 12: Cho hình chóp S. ABC có đáy là ∆ ABC vuông tại C, AB = 5a, BC = 4a Cạnh SA vuông góc với đáy và góc giữa mặt phẳng (SBC) với mặt đáy (ABC) bằng 60°. Gọi D là trung điểm của cạnh AB. Khoảng cách giữa hai đường thẳng SD và BC là:

Bài giải:
+ Gọi M là trung điểm AC, ta có DM là đường trung bình của ∆ ABC nên DM // BC
⇒ BC // (SMD).
⇒ d (BC; SD) = d (C; (SMD)) = d (A; (SMD))
+ Kẻ AH ⊥ SM (H ∈ SM), ta có

Do góc giữa mặt phẳng (SBC) với mặt đáy (ABC) bằng 60° => ∠ SCA = 60°.
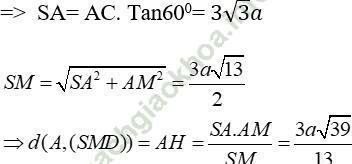
Đáp án đúng là: A
C. Bài tập vận dụng
Câu 1: Cho hình chóp S. ABCD có đáy ABCD là hình chữ nhật và AB = 2a; BC = a. Các cạnh bên của hình chóp bằng nhau và bằng a√ 2. Gọi E và F lần lượt là trung điểm của AB và CD; K là điểm bất kỳ trên BC. Khoảng cách giữa hai đường thẳng EF và SK là:

Gọi O là giao điểm của AC và BD; I là trung điểm cạnh BC
+ Do SA = SB = SC = SD và OA = OB = OC = OD nên SO ⊥ (ABCD)
+ Ta chứng minh BC ⊥ (SOI)
- Tam giác SBC cân tại S có SI là đường trung tuyến nên đồng thời là đường cao: BC ⊥ SI (1).
- Lại có: BC ⊥ SO (vì SO ⊥ (ABCD)) (2)
Từ (1) và (2) suy ra: BC ⊥ (SOI)
Mà OH ⊂ (SOI) nên BC ⊥ OH
⇒ OH ⊥ (SBC)
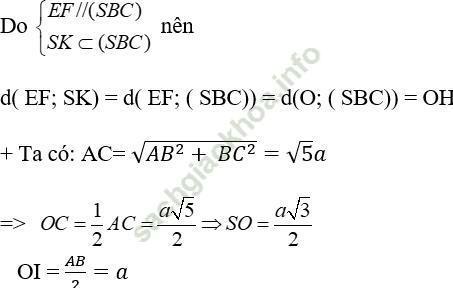
Xét tam giác SOI có:
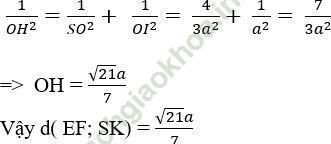
Chọn đáp án D
Câu 2: Cho hình lập phương ABCD. A’B’C’D’ có cạnh bằng 1 (đvd). Khoảng cách giữa AA’ và BD’ bằng:

Ta có: AA’ // DD’ (tính chất hình lập phương)
Mà DD ⊂ (BDD’B’)
⇒ AA’ // (BDD’B’)
⇒ d (AA’; BD’) = d (AA’; (BDD’B’)) = d (A; BDD’B’)
Gọi O là trung điểm của BD
⇒ AO ⊥ BD (tính chất hình vuông)
Lại có: AO ⊥ BB’
⇒ AO ⊥ (BDD’B’)
⇒ d (A; (BDD’B’)) = AO
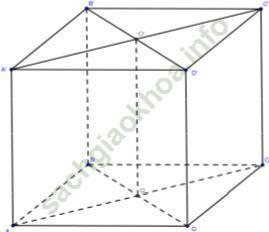
+ Xét tam giác ABD có:
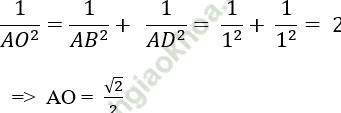
Chọn D
Câu 3: Cho hình chóp S. ABCD có đáy ABCD là hình chữ nhật, BC = a√ 3; AB = a. Hai mặt phẳng (SAC) và (SBD) cùng vuông góc với mặt đáy và đường thẳng SC tạo với mặt đáy một góc 60°. Khoảng cách giữa hai đường thẳng SB và AC.

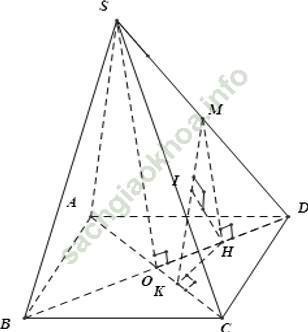
Chọn D
Gọi O là giao điểm của AC và BD
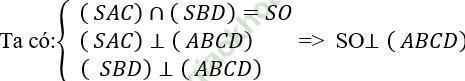
+ Do OC là hình chiếu vuông góc của SC trên mặt phẳng (ABCD) ⇒ (SC, (ABCD)) = ∠ SCO = 60°
+ Gọi M là trung điểm của SD. Khi đó; MO là đường trung bình của tam giác SBD nên MO // SB
⇒ SB // (ACM).
+ Trong mặt phẳng (SBD) kẻ MH // SO
⇒ MH ⊥ (ABCD)
Khi đó
d (SB; AC) = d (SB; (ACM)) = d (B; (ACM)) = 2d (H; (ACM))
+ Ta có: khoảng cách từ D đến AC là d:
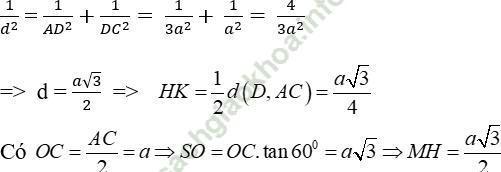
Xét tam giác vuông MHK đường cao MI có:
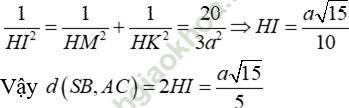
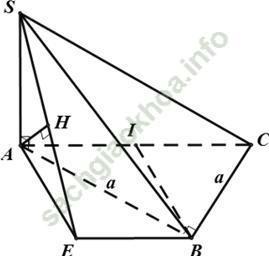
Câu 4: Cho hình chóp S. ABC có đáy ABC là tam giác vuông cân tại B; AB = BC = a, SA vuông góc với mặt phẳng (ABC) góc giữa đường thẳng SC và mặt phẳng (ABC) bằng 60°. Khoảng cách giữa hai đường thẳng SB và AC.

Chọn D
+ Gọi I là trung điểm của AC. Qua B kẻ đường thẳng d song song với AC.
Trong mặt phẳng (ABC) kẻ AE vuông góc với d tại E.
Khi đó AE ⊥ BE và AE ⊥ AC
+ Ta có: AC // BE nên AC // (SBE)
⇒ d (AC, SB) = d (A, (SBE)).
+ Gọi AH là đường cao của (SAE), ta có

Vì SA ⊥ (ABC) nên hình chiếu của SC trên mặt phẳng (ABC) là AC suy ra góc giữa SC và mặt phẳng (ABC) là ∠ SCA = 60°

Câu 5: Cho hình chóp S. ABC có đáy ABC là tam giác cân tại A. Gọi H và M lần lượt là trung điểm các cạnh BC và SC; SH vuông góc với (ABC), SA = 2a và tạo với mặt đáy góc 60°. Khoảng cách giữa hai đường thẳng AM và BC là:

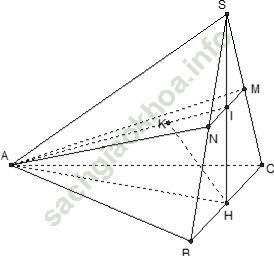
+ Hình chiếu vuông góc của SA trên mặt phẳng (ABC) là HA nên góc giữa SA và (ABC) là ∠ SAH
⇒ suy ra AH = SA. cos60° = a; SH = a√ 3.
+ Gọi N; I lần lượt là trung điểm của SB và SH.
SI = SH/2 = a√ 3/2
Ta có mặt phẳng (AMN) // BC (vì MN // BC)
⇒ d (AM; BC) = d (BC, (AMN)) = d (H; (AMN)).
+ Dựng HK ⊥ AI

+ Xét tam giác IAH vuông tại H, đường cao HK
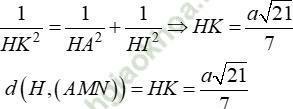
Đáp án C
Câu 6: Cho hình chóp S. ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với mặt phẳng (ABC), gọi I là trung điểm cạnh BC. Biết góc giữa đường thẳng SI và mặt phẳng (ABC) bằng 60°. Khoảng cách giữa hai đường thẳng SB và AC

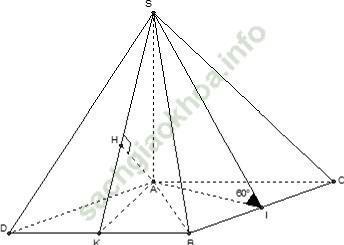
+ Hình chiếu vuông góc của SI trên mặt phẳng (ABC) là AI nên góc giữa SI và mặt phẳng (ABC) là ∠ SIA (vì tam giác SIA vuông tại A nên ∠ SIA nhọn)
Suy ra: ∠ SIA = 60°.
+ Xét tam giác SIA vuông tại A, ∠ SIA = 60° và AI = a√ 3/2 nên SA = AI. tan60° = 3a/2.
+ Dựng hình bình hành ABCD, tam giác ABC đều nên tam giác ABD đều.
+ Ta có AC // BD nên AC // (SBD)
⇒ d (AC; SB) = d (AC, (SBD)) = d (A; (SBD)).
+ Gọi K là trung điểm đoạn BD, tam giác ABD đều cạnh a
suy ra AK ⊥ BD và AK = a√ 3/2 mà BD ⊥ SA nên BD ⊥ (SAK).
+ Dựng AH ⊥ SK, H ∈ SK lại có AH ⊥ BD suy ra AH ⊥ (SBD)
Vậy d (A, (SBD)) = AH
+ Xét tam giác SAK vuông tại vuông tại A, đường cao AH ta có
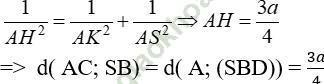
Đáp án B
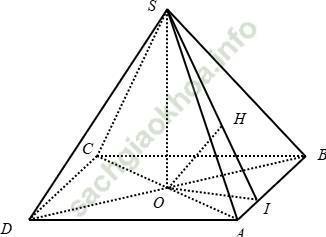
Câu 7: Cho hình chóp S. ABC tam giác ABC vuông tại B; BC = a; AC = 2a tam giác SAB đều. Hình chiếu của S lên mặt phẳng (ABC) trùng với trung điểm M của AC. Khoảng cách giữa hai đường thẳng SA và BC là:

+ Tam giác ABC vuông tại B, BC = a và AC = 2a suy ra AB = a√ 3
Tam giác SAM vuông tại M, SA = a√ 3 (vì tam giác SAB đều); AM = AC/2 = a ⇒ SM = a√ 2
+ Dựng hình bình hành ABCD, gọi N là trung điểm của AD. Do ∠ ABC = 90° suy ra ABCD là hình chữ nhật suy ra MN ⊥ AD.
Lại có: SM ⊥ AD nên AD ⊥ (SMN).
Dựng MH ⊥ AD, H ∈ SN
Theo trên có AD ⊥ (SMN) nên AD ⊥ MH
⇒ MH ⊥ (SAD).
Vậy d (M; (SAD)) = MH.
+ Do BC // AD nên BC // (SAD)
⇒ d (SA; BC) = d (BC; (SAD) = d (C; (SAD))
= 2d (M; (SAD)) = 2. MH
+ Xét tam giác SMN vuông tại M, đường cao MH:
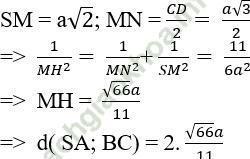
Chọn C
Câu 8: Cho hình chóp S. ABCD có đáy ABCD là hình thoi cạnh a và ∠ ABC = 60°. Hai mặt phẳng (SAC) và (SBD) cùng vuông góc với đáy, góc giữa hai mặt phẳng (SAB) và (ABCD) bằng 30°. Khoảng cách giữa hai đường thẳng SA và CD theo a bằng:

Gọi O là giao điểm của AC và BD
Kẻ: OI ⊥ AB; OH ⊥ SI

+ Do CD // AB nên CD // (SAB)
⇒ d (CD; SA) = d (CD, (SAB))
= d (C; (SAB)) = 2d (O; (SAB))
Ta có: AB ⊥ SO, AB ⊥ OI ⇒ AB ⊥ (SOI) ⇒ AB ⊥ OH
Nên OH ⊥ (SAB) ⇒ d (O, (SAB)) = OH
Mà tam giác ACB cân tại B có ∠ ABC = 60° nên tam giác ABC đều
⇒ OC = (1/2)AC = (1/2)AB = a/2
+ xét tam giác OAB có:

Chọn đáp án B
Câu 9: Cho hình chóp S. ABCD có đáy ABCD là hình thoi tâm I, AB = 2a; BD = √ 3AC, mặt bên SAB là tam giác cân đỉnh A; hình chiếu vuông góc của đỉnh S trên mặt phẳng đáy trùng với trung điểm H của AI. Khoảng cách giữa hai đường thẳng SB và CD bằng:

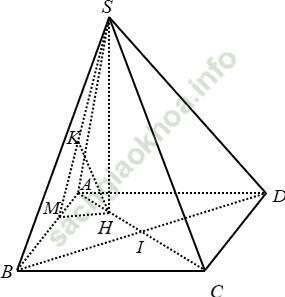
+ Ta có: CD // AB ⇒ CD // (SAB)
⇒ d (CD; SB) = d (CD; (SAB)) = d (C; (SAB)) = 4. d (H; (SAB))
+ Kẻ MH ⊥ AB; HK ⊥ SM

Ta có: tan (BAC) = BI/IA = √ 3 ⇒ ∠ BAC = 60° ⇒ Δ ABC đều
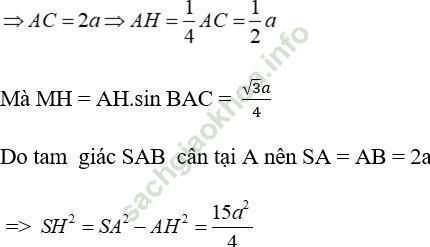
Do đó:
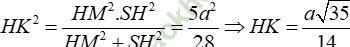
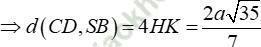
Chọn đáp án B
Câu 10: Cho hình chóp S. ABCD có đáy là hình vuông ABCD cạnh a. Các cạnh bên SA = SB = SC = SD = a√ 2. Khoảng cách giữa hai đường thẳng AD và SB là:

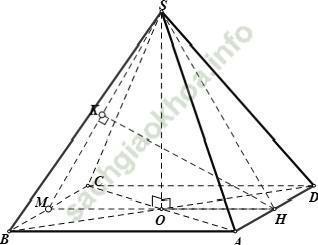
+ Do AD // BC nên AD // (SBC)
⇒ d (AD; SB) = d (AD, (SBC)) = d (H; (SBC))
Trong đó H là trung điểm AD.
+ Gọi M là trung điểm của BC và K là hình chiếu vuông góc của H lên SM
⇒ d (H; (SBC)) = HK.
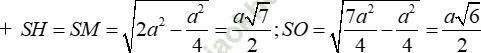
+ Diện tích tam giác SMH là: