Dạng 1:Đếm số phương án liên quan đến số tự nhiên - Chuyên đề Toán 11
A. Phương pháp giải & Ví dụ
Ta sử dụng phương pháp chung và có một số lưu ý như sau:
- Khi lập một số tự nhiên ![]() ta cần lưu ý:
ta cần lưu ý:
* ai ∈ {0,1,2, …, 9} và a1 ≠ 0.
* x là số chẵn ⇔ an là số chẵn.
* x là số lẻ ⇔ an là số lẻ.
* x chia hết cho 3 ⇔ a1+a2+⋯+an chia hết cho 3.
* x chia hết cho 4 ⇔ ![]() chia hết cho 4.
chia hết cho 4.
* x chia hết cho 5 ⇔ an = 0 hoặc an = 5.
* x chia hết cho 6 ⇔ x là số chẵn và chia hết cho 3.
* x chia hết cho 8 ⇔ ![]() chia hết cho 8.
chia hết cho 8.
* x chia hết cho 9 ⇔ a1+a2+⋯+an chia hết cho 9.
* x chia hết cho 11⇔ tổng các chữ số ở hàng lẻ trừ đi tổng các chữ số ở hàng chẵn là một số chia hết cho 11.
* x chia hết cho 25 ⇔ hai chữ số tận cùng là 00,25,50 hoặc 75.
Ví dụ minh họa
Bài 1: Có bao nhiêu chữ số chẵn gồm bốn chữ số đôi một khác nhau được lập từ các số 0,1,2,4,5,6,8.
Bài giải:
a, b, c, d ∈ {0,1,2,4,5,6,8}, a ≠ 0.
Vì x là số chẵn nên d ∈ {0,2,4,6,8}.
TH1: d = 0 ⇒ Có 1 cách chọn d.
Vì a ≠ 0 nên ta có 6 cách chọn a ∈ {1,2,4,5,6,8}.
Với mỗi cách chọn a, d ta có 5 cách chọn b ∈ {1,2,4,5,6,8}\ {a}.
Với mỗi cách chọn a, b, d ta có 4 cách chọn c ∈ {1,2,4,5,6,8}\ {a, b}.
=> Có 1.6.5.4 = 120 số.
TH2: d ≠ 0, d chẵn nên d ∈ {2,4,6,8}. Vậy có 4 cách chọn d
Với mỗi cách chọn d, do a ≠ 0 nên ta có 5 cách chọn a ∈ {1,2,4,5,6,8}\ {d}.
Với mỗi cách chọn a, d ta có 5 cách chọn b ∈ {0,1,2,4,5,6,8}\ {a, d}.
Với mỗi cách chọn a, b, d ta có 4 cách chọn c ∈ {0,1,2,4,5,6,8}\ {a, d, b}.
=> Có 4.5.5.4= 400 số.
Vậy có tất cả 120 + 400 = 520 số cần lập.
Bài 2: Cho tập A = {0,1,2,3,4,5,6}. Từ tập A ta có thể lập được bao nhiêu số tự nhiên gồm 4 chữ số đôi một khác nhau.
Bài giải:
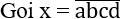
a, b, c, d ∈ {0,1,2,3,4,5,6}, a ≠ 0.
Vì a ≠ 0 nên a có 6 cách chọn a ∈ {1,2,3,4,5,6}.
Với mỗi cách chọn a ta có 6 cách chọn b ∈ {0,1,2,3,4,5,6}\ {a}.
Với mỗi cách chọn a, b ta có 5 cách chọn c ∈ {0,1,2,3,4,5,6}\ {a, b}.
Với mỗi cách chọn a, b, c ta có 4 cách chọn d ∈ {0,1,2,3,4,5,6}\ {a, b, c}.
Vậy có 6.6.5.4 = 720 số cần lập.
Bài 3: Cho tập A = {1,2,3,4,5,6,7,8}.
Từ tập A có thể lập được bao nhiêu số gồm 8 chữ số đôi một khác nhau sao các số này lẻ không chia hết cho 5.
Bài giải:
a, b, c, d, e, f, g, h ∈ {1,2,3,4,5,6,7,8} là số cần tìm.
Vì x lẻ và không chia hết cho 5 nên h ∈ {1,3,7} nên h có 3 cách chọn
Số các chọn các chữ số còn lại là: 7.6.5.4.3.2.1
Vậy có tất cả 15120 số thỏa yêu cầu bài toán.
B. Bài tập vận dụng
Bài 1: Cho tập A = {0,1,2,3,4,5,6}. Từ tập A ta có thể lập được bao nhiêu số tự nhiên lẻ gồm 4 chữ số đôi một khác nhau
Bài giải:
a, b, c, d ∈ {0,1,2,3,4,5,6}, a ≠ 0
Vì x là số lẻ nên d ∈ {1,3,5} vậy d có 3 cách chọn.
Vì a ≠ 0 và với mỗi cách chọn d ta có 5 cách chọn a ∈ {1,2,3,4,5,6}\ {d}.
Với mỗi cách chọn a, d ta có 5 cách chọn b ∈ {0,1,2,3,4,5,6}\ {a, d}.
Với mỗi cách chọn a, b, d ta có 4 cách chọn c ∈ {0,1,2,3,4,5,6}\ {a, b, d}.
=> Có tất cả: 3.5.5.4 = 300 số.
Bài 2: Cho tập A = {0,1,2,3,4,5,6}. Từ tập A có thể lập được bao nhiêu số tự nhiên gồm 5 chữ số và chia hết cho 5.
Bài giải:
a, b, c, d, e ∈ {0,1,2,3,4,5,6}, a ≠ 0 là số cần lập, e ∈ {0,5}.
TH1: e = 0 suy ra có 1 cách chọn, số cách chọn a, b, c, d là 6.5.4.3
Có: 360 số thỏa mãn yêu cầu bài toán.
TH2: e = 5 suy ra e có 1 cách chọn, số cách chọn a, b, c, d là 5.5.4.3 = 300.
=> Có 300 số thỏa mãn yêu cầu bài toán
Vậy có tất cả: 360+300 = 660 số thỏa yêu cầu bài toán.
Bài 3: Cho tập hợp số A = {0,1,2,3,4,5,6}. Hỏi có thể thành lập bao nhiêu số có 4 chữ số khác nhau và chia hết cho 3.
Bài giải:
Ta có một số chia hết cho 3 ⇔ Tổng các chữ số chia hết cho 3.
Trong tập A có các tập con các chữ số chia hết cho 3 là {0,1,2,3}, {0,1,2,6}, {0,2,3,4}, {0,3,4,5}, {1,2,4,5}, {1,2,3,6}, {1,3,5,6}.
Vậy số các số cần lập là: 4 (4! – 3! ) + 3.4! = 144 số.
Bài 4: Có bao nhiêu số các số tự nhiên gồm chữ số chia hết cho 10?
Bài giải:
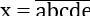
a, b, c, d, e là các chữ số, a ≠ 0.
Vì x chia hết cho 10 nên e = 0, vậy e có 1 cách chọn.
Chọn a có 9 cách chọn a ∈ {1,2,3,4,5,6,7,8,9}.
Chọn b có 10 cách chọn b ∈ {0,1,2,3,4,5,6,7,8,9}.
Chọn c có 10 cách chọn c ∈ {0,1,2,3,4,5,6,7,8,9}
Chọn d có 10 cách chọn d ∈ {0,1,2,3,4,5,6,7,8,9}
=> Có tất cả 1.9.10.10.10 = 9000 số thỏa mãn yêu cầu bài ra.
Bài 5: Cho tập A = {1,2,3,4,5,6,7,8}. Từ tập A có thể lập được bao nhiêu số gồm 8 chữ số đôi một khác nhau sao cho chữ số đầu chẵn và chữ số đứng cuối lẻ.
Bài giải:
a, b, c, d, e, f, g, h ∈ {1,2,3,4,5,6,7,8} là số cần tìm.
Vì chữ số đứng đầu chẵn nên a có 4 cách chọn,
Chữ số đứng cuối lẻ nên h có 4 cách chọn.
Các số còn lại có 6.5.4.3.2.1 cách chọn
=> Có tất cả: 42.6.5.4.3.2.1 = 11520 số thỏa yêu cầu bài toán.