Giá trị lớn nhất, nhỏ nhất của hàm số lượng giác - Chuyên đề Toán 11
A. Phương pháp giải
Để tìm được giá trị lớn nhất; giá trị nhỏ nhất của hàm số ta cần chú ý:
+ Với mọi x ta luôn có: - 1 ≤ cosx ≤ 1; -1 ≤ sinx ≤ 1
+ Với mọi x ta có: 0 ≤ |cosx| ≤ 1; 0 ≤ |sinx| ≤ 1
+ Bất đẳng thức bunhia –copski: Cho hai bộ số (a1; a2) và (b1;b2) khi đó ta có:
(a1.b1+ a2.b2)2 ≤ (a12+ a22). (b12+ b22)
Dấu “=” xảy ra khi: a1/a2 = b1/b2
+ Giả sử hàm số y = f (x) có giá trị lớn nhất là M và giá trị nhỏ nhất là m. Khi đó; tập giá trị của hàm số là [m; M].
+ Phương trình: a. sinx+ b. cosx= c có nghiệm khi và chỉ khi a2 + b2 ≥ c2
B. Ví dụ minh họa
Ví dụ 1. Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số y = 1 - 2|cos3x|.
A. M = 3; m = - 1.
B. M = 1; m = -1.
C. M = 2; m = -2.
D. M = 0; m = -2.
Bài giải:
Đáp án đúng là: B.
Giải thích:
Với mọi x ta có: - 1 ≤ cos3x ≤ 1 nên 0 ≤ |cos3x| ≤ 1
⇒ 0 ≥ -2|cos3x| ≥ -2
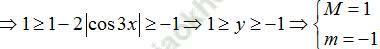
Ví dụ 2: Hàm số y = 1 + 2cos2x đạt giá trị nhỏ nhất tại x = x0. Mệnh đề nào sau đây là đúng?
A. x0 = π + k2π, kϵZ.
B. x0 = π /2 + kπ, kϵZ.
C. x0 = k2π, kϵZ.
D. x0 = kπ, kϵZ.
Bài giải:
Đáp án đúng là: B.
Giải thích:
Ta có - 1 ≤ cosx ≤ 1 ⇒ - 0 ≤ cos2x ≤ 1 ⇒ 1 ≤ 1 + 2cos2x ≤ 3
Do đó giá trị nhỏ nhất của hàm số bằng 1.
Dấu "=" xảy ra khi cosx = 0 ⇒ x = π /2 + kπ, kϵZ.
Ví dụ 3: Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số y = sin2x + 2cos2x.
A. M = 3; m = 0
B. M = 2; m = 0.
C. M = 2; m = 1.
D. M = 3; m = 1.
Bài giải:
Đáp án đúng là: C.
Giải thích:
Ta có: y = sin2 x + 2cos2x = (sin2x + cos2x) + cos2x = 1 + cos2 x.
Do: -1 ≤ cosx ≤ 1 nên 0 ≤ cos2 x ≤ 1 ⇒ 1 ≤ cos2 x + 1 ≤ 2
=> Giá trị lớn nhất của hàm số là M = 2 và giá trị nhỏ nhất của hàm số là m = 1
Ví dụ 4: Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số y = 4sinx - 3
A. M = 1; m = - 7
B. M = 7; m = - 1
C. M = 3; m = - 4
D. M = 4; m = -3
Bài giải:
Đáp án đúng là: A
Ta có: - 1 ≤ sinx ≤ 1 nên - 4 ≤ 4sinx ≤ 4
Suy ra: - 7 ≤ 4sinx-3 ≤ 1
Do đó: M= 1 và m = - 7
Ví dụ 5: Tìm tập giá trị T của hàm số y = -2cos2x + 10.
A. [5; 9]
B. [6; 10]
C. [ 8; 12]
D. [10; 14]
Bài giải:
Đáp án đúng là: C
Giải thích:
Với mọi x ta có: - 1 ≤ cos2x ≤ 1 nên -2 ≤ -2cos2x ≤ 2
⇒ 8 ≤ -2cos2x + 10 ≤ 12
Do đó: Tập giá trị của hàm số đã cho là: T= [8; 12]
Ví dụ 6: Tính độ dài giá trị của hàm số y = 10 - 2cos2x
A. 10
B. 8
C. 6
D. 4
Bài giải:
Đáp án đúng là: D
Giải thích:
Với mọi x ta có: - 1 ≤ cos2x ≤ 1 nên -2 ≤ -2cos2x ≤ 2
Suy ra: 8 ≤ 10 - 2cos2x ≤ 12
Do đó: Tập giá trị của hàm số đã cho là: [8; 12] và độ dài đoạn giá trị của hàm số là:
12 – 8= 4
Ví dụ 7: Tính tổng giá trị nhỏ nhất m và giá trị lớn nhất M của hàm số sau: y= √ 3 sin (2016x+2019)
A. - 4032
B. √ 3
C. -√ 3
D. 0
Bài giải:
Đáp án đúng là: D
Giải thích:
Với mọi x ta có: - 1 ≤ sin (2016x + 2019) ≤ 1
⇒ -√ 3 ≤ √ 3sin (2016x + 2019) ≤ √ 3
Do đó giá trị nhỏ nhất của hàm số là -√ 3 và giá trị lớn nhất của hàm số là √ 3
⇒ Tổng giá trị lớn nhất và nhỏ nhất của hàm số là - √ 3 + √ 3=0
Ví dụ 8: Tìm giá trị nhỏ nhất m của hàm số y = 1/ (1 + sinx)
A. m = 1/2
B. m = 1/√ 2
C. m = 1
D. m = √ 2
Bài giải:
Đáp án đúng là: A
Điều kiện xác định: sinx ≠ -1 hay x ≠ (- π)/2 + k2π
+ Với mọi x thỏa mãn điều kiện ta có: - 1< sinx ≤ 1 nên sinx + 1 > 0
+ Nếu mẫu 1+ sinx > 0 thì hàm số đạt giá trị nhỏ nhất khi và chỉ khi 1+ sinx đạt giá trị lớn nhất
Hay 1+ sinx = 2 < => sinx = 1 (thỏa mãn điều kiện).
Khi đó ymin = 1/2
Vậy hàm số đạt giá trị nhỏ nhất là 1/2 khi sinx = 1
Ví dụ 9: Tìm giá trị lớn nhất M, giá trị nhỏ nhất m của hàm số:
y = 2018sin (9x + π/100) + 2000
A. m = 18; M = 4018
B. m = -18; M = 18
C. m = -18; M = 4018
D. Đáp án khác
Bài giải:
Đáp án đúng là: C
Giải thích:
Hàm số xác định trên R.
Với mọi x ta có: - 1 ≤ sin (9x+π/100) ≤ 1 nên - 2018 ≤ 2018sin (9x+π/100) ≤ 2018
⇒ -18 ≤ 2018sin (9x + π/100) + 2000 ≤ 4018
⇒ Giá trị nhỏ nhất của hàm số là -18 khi sin (9x + π/100) = -1
Giá trị lớn nhất của hàm số là 4018 khi sin (9x + π/100) = 1
Ví dụ 10: Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số y = ∜sinx - √ cosx.
A. m = -1; M = 1.
B. m = 0; M = 1
C. m = -1; M = 0
D. m = -1 và M không tồn tại.
Bài giải:
Đáp án đúng là: A
Giải thích:
Với mọi x thỏa mãn điều kiện: sinx > 0 và cosx > 0. Ta có:
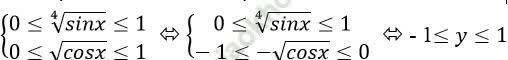
Vậy hàm số đạt giá trị nhỏ nhất là m = – 1 khi: (sinx = 0 và cosx = 1 ⇒ x = k2π.
Hàm số đạt giá trị lớn nhất là M = 1 khi (sinx = 1 và cosx = 0 ⇒ x = π/2 + k2π.
Ví dụ 11. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số:
y= cos2 x – 6cosx + 11. Tính M. m
A. 30
B. 36
C. 27
D. 24
Bài giải:
Đáp án đúng là: B
Giải thích:
Ta có: cos2 x – 6cosx +11 = (cos2x – 6cosx + 9) +2 = (cosx -3)2 + 2
Do - 1 ≤ cosx ≤ 1 ⇒ - 4 ≤ cosx - 3 ≤ -2
⇒ 0 ≤ (cosx - 3)^2 ≤ 16
⇒ 2 ≤ (cosx - 3)^2 + 2 ≤ 18
Suy ra: M = 18 và m = 2 nên M. m = 36.
Ví dụ 12. Gọi M và lần lượt là giá trị lớn nhất; giá trị nhỏ nhất của hàm số
y= (cosx + 2sinx + 3)/ (2cosx - sinx + 4). Tính S = M + 11m
A. 4
B. 5
C. 6
D. 8
Bài giải:
Đáp án đúng là: A
Giải thích:
Gọi y0 là một giá trị của hàm số.
Khi đó phương trình y0 = (cosx + 2sinx + 3)/ (2cosx - sinx + 4) có nghiệm.
⇒ y0. (2cosx - sinx + 4) = cosx + 2sinx + 3 có nghiệm
⇒ 2y0.cosx – sinx. y0 + 4y0- cosx – 2sinx – 3 = 0 có nghiệm
⇒ (2y0 - 1)cosx – (y0 + 2).sinx = 3 - 4y0 (*)
Phương trình (*) có nghiệm khi và chỉ khi:
(2y0-1)2 + (y0 + 2)2 ≥ (3-4y0)2
⇒ 4y02 – 4y0 +1 + y02 + 4y0 + 4 ≥ 9 - 24y0 + 16y02
⇒ 11y02 – 24y0 + 4 ≤ 0 ⇒ 2/11 ≤ y0 ≤ 2
Suy ra: M = 2 và m = 2/11 nên S = M + 11m = 4
Ví dụ 13. Cho hàm số y= √ (1+2sin2 x)+ √ (1+2〖cos2 x)-1. Gọi m và M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số. Khi đó; giá trị M+ m gần với giá trị nào nhất?
A. 3,23
B. 3,56
C. 2,78
D. 2,13
Bài giải:
Đáp án đúng là: B
Giải thích:
+ Xét t= √ (1+2sin2 x)+ √ (1+2cos2 x)
⇒ t2 = 1+ 2sin2 x+ 1+ 2cos2 x+ 2. √ ((1+2sin2 x). (1+2cos2 x))
=4+2√ (3+ sin2 2x)
Mà sin22x ≥ 0 nên t2 ≥ 4+ 2√ 3
Mà t > 0 nên t ≥ √ (4+2√ 3) =1+ √ 3
Suy ra: y= t-1 ≥ √ 3
Dấu “=” xảy ra khi sin2x=0.
+ Lại có:
√ (1+2sin2 x)+ √ (1+2cos2 x) ≤ √ ((1^2+ 1^2). (1+2sin2x+ 1+2cos2 x))= 2√ 2
⇒ y= √ (1+2sin2 x)+ √ (1+2cos2 x)-1 ≤ 2√ 2-1
Dấu “=” xảy ra khi sin2 x= cos2x
Vậy {(m= √ 3 và M=2√ 2-1) ⇒ M+ m≈3,56
C. Bài tập vận dụng
Câu 1: Gọi M; m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = 8sin2x + 3cos2x. Tính P = M - 2m.
A. P= - 1
B. P= 1
C. P= 2
D. P=0
Chọn A.
Ta có: y = 8sin2 x + 3cos2x = 8sin2x + 3 (1 – 2sin2x) = 2sin2x+ 3.
Mà -1 ≤ sinx ≤ 1 ⇒ 0 ≤ sinx ≤ 1 ⇒ 3 ≤ 2sinx+3 ≤ 5 ⇒ 3 ≤ y ≤ 5.
Suy ra: M= 5 và m= 3
Do đó: P = 5- 2.3= - 1
Câu 2: Tìm giá trị lớn nhất M của hàm số y= 4sin2x + 3. cos2x.
A. M= 3
B. M= 1
C. M= 5
D. M= 4
Chọn C.
Ta có: y = 4sin2x+ 3cos2x = 5. ( 4/5. sin2x+ 3/5 cos2x).
Đặt cosα= 4/5 và sinα= 3/5
Khi đó: y= 5 (cosα. sin2x+sinα. cos2x)=5. sin (α+2x)
⇒ - 5 ≤ y ≤ 5
Suy ra M= 5.
Câu 3: Gọi M; m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y= sin2x – 4sinx+ 5. Tính M+ m.
A. 3
B. 8
C. 10
D. 12
Chọn D.
Ta có: y= sin2x – 4sinx+ 5= (sinx- 2)2 + 1.
Do: -1 ≤ sinx ≤ 1 nên-3 ≤ sinx-2 ≤ -1
⇒ 1 ≤ (sinx-2)2 ≤ 9 ⇒ 2 ≤ (sinx-2)2+1 ≤ 10.
Suy ra: M=10 và m = 2
Do đó; M+ m = 12
Câu 4: Cho hàm số y= cos2x- cosx có tập giá trị là T. Hỏi có tất cả bao nhiêu giá trị nguyên thuộc T.
A. 1
B. 2
C. 3
D. 4
Chọn C.
Ta có: cos2x- cosx = (cosx- 1/2)2- 1/4.
Do - 1 ≤ cosx ≤ 1 nên (- 3)/2 ≤ cosx- 1/2 ≤ 1/2
⇒ 0 ≤ (cosx- 1/2)2 ≤ 9/4 ⇒ (- 1)/4 ≤ (cosx- 1/2)2- 1/4 ≤ 2.
Do đó (- 1)/4 ≤ y ≤ 2. Vậy tập giá trị của hàm số là [(- 1)/4; 2]
⇒ Trong đoạn [-1/4; 2] có ba giá trị nguyên thỏa mãn là 0; 1 và 2.
Do đó có 3 giá trị thỏa mãn.
Câu 5: Hàm số y= cos2x+ 2sinx+ 2 đạt giá trị nhỏ nhất tại x0. Mệnh đề nào sau đây là đúng.
A. x= (-π)/2+k2π.
B. x= π/2+k2π.
C. x= k π
D. x= k2π
Chọn B.
Ta có: cos2x+ 2sinx+ 2 = 1- sin2x+ 2sinx + 2= - sin2x + 2sinx+ 3 = - (sinx-1)2 + 4
Mà - 1 ≤ sinx ≤ 1 nên-2 ≤ sinx-1 ≤ 0
Suy ra: 0 ≤ (sinx-1)2 ≤ 4 ⇒ -4 ≤ - (sinx-1)2 ≤ 0
⇒ 0 ≤ 4 - (sinx-1)2 ≤ 4
Suy ra giá trị nhỏ nhất của hàm số bằng 0.
Dấu “=” xảy ra khi và chỉ khi sinx= 1 ⇒ x= π/2+k2π.
Câu 6: Tìm giá trị lớn nhất M và nhỏ nhất m của hàm số y= sin4x -2 cos2x+ 1.
A. M= 2; m= - 2
B. M=1; m=0
C. M=4; m= - 1
D M=2; m= - 1
Chọn D.
Ta có: sin4x- 2cos2x + 1= sin4x – 2 (1- sin2x) + 1
= sin4x + 2sin2x - 1 = (sin2 x +1)22 - 2
Mà: 0 ≤ sin2 x ≤ 1 nên 1 ≤ sin2 x+1 ≤ 2
Suy ra: 1 ≤ (sin2 x+1)2 ≤ 4 ⇒ -1 ≤ (sin2 x+1)2-2 ≤ 2.
Nên M= 2; m= - 1
Câu 7:Tìm giá trị nhỏ nhất của hàm số y= 4sin4x – cos4x.
A. - 3
B. - 1
C. 3
D. 5
Chọn B.
Ta có: y= 4sin4x – cos4x= 4. ( (1-cos2x)/2)2- (2cos2 2x-1)
= 1- 2cos2x+ cos22x – 2cos2x + 1
= - cos42x - 2cos2x + 2 = - (cos2x+ 1)2 + 3
Mà -1 ≤ cos2x ≤ 1 ⇒ 0 ≤ cos2x+1 ≤ 2 ⇒ 0 ≤ (cos2x+1)2 ≤ 4 ⇒ -1 ≤ - (cos2x+1)2+3 ≤ 3
Suy ra m= - 1.
Câu 8: Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y= 2 (sinx - cosx). Tính P= M+ 2m.
A. 2
B. - 2√ 2
C. - √ 2
D. 4√ 2
Chọn B
Ta có: 2 (sinx- cosx)=2√ 2 sin (x- π/4)
Với mọi x thì: - 1 ≤ sin (x- π/4) ≤ 1
⇒ - 2√ 2 ≤ 2√ 2. sin (x- π/4) ≤ 2√ 2
Vậy giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho là M= 2√ 2 và m= -2√ 2
⇒ P= M+ 2m= - 2√ 2
Câu 9: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y= √ (1- cos2 x)+1là:
A. 2 và 1
B. 0 và 3
C. 1 và 3
D. 1 và 1+ √ 2
Ta có: √ (1- cos2 x)= √ (sin2 x)= |sinx|
Do đó; hàm số y= √ (1- cos2 x)+1=|sinx|+1
Với mọi x ta có: - 1 ≤ sinx ≤ 1 nên 0 ≤ |sinx| ≤ 1
⇒ 1 ≤ |sinx|+1 ≤ 2
⇒ giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho là 2 và 1.
Chọn A
Câu 10: Giá trị nhỏ nhất của hàm số y= 4sin2 x+ 6cos2x+ 2 là
A. 4
B. 6
C. 8
D. 10
Ta có: 4sin2x + 6cos2 x+ 1= 2 (1- cos2x) + 3 (1+cos2x) + 2 = cos2x+ 7
Với mọi x ta luôn có: - 1 ≤ cos2x ≤ 1 nên 6 ≤ cos2x+7 ≤ 8
Suy ra: giá trị nhỏ nhất của hàm số là 6
Chọn B.
Câu 11:Tìm tập giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau
A. max y=4, min y=3/4
B. max y=3, min y=2
C. max y=4, min y=2
D. max y=3, min y=3/4
Đặt t=sin2x, 0 ≤ t ≤ 1 ⇒ cos2x=1-2t
⇒ y= 2t+ (1-2t)2=42-2t+1= (2t-1/2)2+3/4
Do 0 ≤ t ≤ 1 ⇒ -1/2 ≤ 2t-1/2 ≤ 3/2 ⇒ 0 ≤ (2t-1/2)2 ≤ 9/4 ⇒ 3/4 ≤ y ≤ 3.
Vậy max y=3 đạt được khi x=π /2+kπ.
min y=3/4 đạt được khi sin2x=1/4.
Chọn D.Câu 12: Tìm tập giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau y = 3sinx + 4cosx + 1
A. max y=6, min y=-2
B. max y=4, min y=-44
C. max y=6, min y=-4
D. max y=6, min y=-1
Áp dụng bất đẳng thức bunhia- xcopski: (ac+bd)2 ≤ (c2+d2) (a2+b2).
Đẳng thức xảy ra khi a/c=b/d.
Ta có: (3sinx+4cosx)2 ≤ (32+42) (sin2+cos2)=25
⇒ 5 ≤ 3sinx+4cosx ≤ 5 ⇒ -4 ≤ y ≤ 6
Vậy max y=6, đạt được khi tanx=3/4.
min y=-4, đạt được khi tanx=-3/4.
Chọn C.
Câu 13: Tìm tập giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau y=2sin2x+3sin2x-4cos2x
A. min y= -3√ 2 -1, max y=3√ 2 +1
B. min y= -3√ 2 -1, max y=3√ 2 -1
C. min y= -3√ 2, max y=3√ 2 -1
D. min y= -3√ 2 -2, max y=3√ 2 -1
Ta có: y= 2sin2 x + 3sin2x - 4cos2x
= 1 – cos2x + 3sin2x - 2 (1+ cos2x)
=3sin2x-3cos2x-1=3√ 2sin (2x-π/4)-1
Mà -1 ≤ sin (2x- π/4) ≤ 1 ⇒ - 3√ 2 ≤ 3√ 2sin (2x- π/4) ≤ 3√ 2
⇒ - 3√ 2-1 ≤ 3√ 2sin (2x- π/4)-1 ≤ 3√ 2-1
Suy ra min y= -3√ 2 -1, max y=3√ 2 -1.
Chọn B.
Câu 14: Tìm tập giá trị lớn nhất, giá trị nhỏ nhất của hàm số y=sin2x+3sin2x+3cos2x
A. min y= 2+√ 10, max y=2-√ 10
B. min y= 2+√ 5, max y=2+√ 5
C. min y= 2+√ 2, max y=2-√ 2
D. min y= 2+√ 7, max y=2-√ 7
Ta có: IMG_2
Áp dụng bất đẳng thức bunhia- xcopki ta có:
- √ (32+ 12) ≤ 3sin2x+cos2x ≤ √ (32+ 12)
Suy ra: -√ 10 ≤ 3sin2x+cos2x ≤ √ 10
⇒ 2-√ 10 ≤ y ≤ 2+√ 10
Từ đó ta có được: maxy=2+√ 10; miny=2-√ 10.
Chọn A.
Câu 15: Tìm tập giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau y=sinx+ √ (2-sin2)
A. min y= 0, max y=3
B. min y= 0, max y=4
C. min y= 0, max y=6
D. min y= 0, max y=2
Ta có 0 ≤ y ∀ x và y2=2+2sin√ (2-sin2)
Mà 2|sin√ (2-sin2)| ≤ sin2+2-sin2=2
Suy ra 0 ≤ y2 ≤ 4 ⇒ 0 ≤ y ≤ 4
min y=0 đạt được khi x=-π/2+k2π
max y=2 đạt được khi x=π/2+k2π
Chọn D.
Câu 16:Tìm tập giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau y= (sin2x+2cos2x+3)/ (2sin2x-cos2x+4)
A. min y= -2/11, max y=2
B. min y= 2/11, max y=3
C. min y= 2/11, max y=4
D. min y= 2/11, max y=2
+ Áp dụng bất đẳng thức bunhia-xcopski ta có:
(2sin2x – cos2x)2 ≤ (22+ (-1)2). ( sin22x + cos22x) = 5
⇒ -√ 5 ≤ 2sin2x-cos2x ≤ √ 5
⇒ 4-√ 5 ≤ 4+ 2sin2x-cos2x ≤ 4+√ 5
⇒ 4+ 2sin2x- cos2x > 0 với mọi x.
+ Ta có:
y= (sin2x+2cos2x+3)/ (2sin2x-cos2x+4)
⇒ y. 2sin2x – y. cos2x + 4y = sin2x +2cos2x + 3
⇔ (2y-1)sin2x- (y+2)cos2x=3-4y (*)
Phương trình (*) có nghiệm khi và chỉ khi:
⇒ (2y-1)2+ (y+2)2 ≥ (3-4y)2
⇔ 11y2-24y+4 ≤ 0 ⇔ 2/11 ≤ y ≤ 2
Suy ra: min y= 2/11, max y=2.
Chọn D.
Câu 17:Tìm tập giá trị lớn nhất, giá trị nhỏ nhất của hàm số y= (2sin23x+4sin3xcos3x+1)/ (sin6x+4cos6x+10)
A. min y= (11-9√ 7)/83, max y= (11+9√ 7)/83
B. min y= (22-9√ 7)/11, max y= (22+9√ 7)/11
C. min y= (33-9√ 7)/83, max y= (33+9√ 7)/83
D. min y= (22-9√ 7)/83, max y= (22+9√ 7)/83
+Áp dụng bất đẳng thức bunhia- xcopski ta có:
( sin6x+4cos6x)2 ≤ (12+42). ( sin26x+ cos26x)= 17
⇒ -√ 17 ≤ sin6x+4cos6x ≤ √ 17
⇒ sin6x+4cos6x+10 ≥ 10-√ 17 > 0 ∀ x thuộc R
Do đó; hàm số xác định với mọi x.
+ ta có: y= (2sin6x-cos6x+2)/ (sin6x+4cos6x+10)
⇒ (y-2)sin6x+ (4y+1)cos6x=2-10y
Phương trình trên có nghiệm khi và chỉ khi:
⇒ (y-2)2+ (4y+1)2 ≥ (2-10y)2 ⇔ 83y2-44y-1 ≤ 0
⇒ (22-9√ 7)/83 ≤ y ≤ (22+9√ 7)/83.
Suy ra: min y= (22-9√ 7)/83, max y= (22+9√ 7)/83