Trang chủ > Lớp 11 > Chuyên đề Toán 11 (có đáp án) > Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa - Chuyên đề Toán 11

Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa - Chuyên đề Toán 11

A. Phương pháp giải & Ví dụ

- Để chứng minh limun = 0 ta chứng minh với mọi số a > 0 nhỏ tùy ý luôn tồn tại một số na sao cho |un|< a ∀ n > na.

- Để chứng minh limun = 1 ta chứng minh lim (un-1) = 0.

- Để chứng minh limun = +∞ ta chứng minh với mọi số M > 0 lớn tùy ý, luôn tồn tại số tự nhiên nM sao cho un > M ∀ n > nM.

- Để chứng minh limun = -∞ ta chứng minh lim (-un) = +∞

- Một dãy số nếu có giới hạn thì giới hạn đó là duy nhất.

Ví dụ minh họa

Bài 1: Chứng minh rằng:

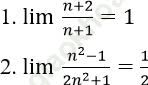
Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 1

Bài giải:

1. Với a > 0 nhỏ tùy ý, ta chọn: Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 2

Ta có:

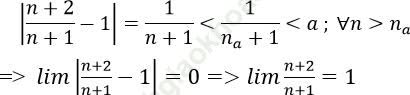
Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 3

2. Với a > 0 nhỏ tùy ý, ta chọn:

Ta có:

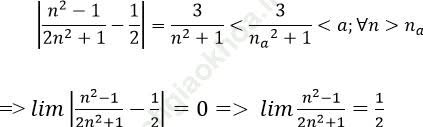
Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 5

Bài 2: CMR: dãy số (un): un = (-1)n không có giới hạn.

Bài giải:

Ta có: u2n = 1 ⇒ limu2n = 1; u(2n+1) = -1 ⇒ limu(2n+1) = -1

Vì giới hạn của dãy số nếu có là duy nhất nên => Dãy (un) không có giới hạn.

Bài 3: Chứng minh các giới hạn sau:

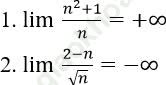
Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 6

Bài giải:

1. Với ∀ số thực dương M lớn tùy ý, ta có:

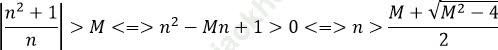
Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 7

Chọn: Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 8

=> Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 9

2. Với ∀ M > 0 lớn tùy ý, ta có:

Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 10

Ta chọn: Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 11

Do đó: Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 12

Bài 4: CMR:

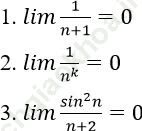
Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 13

Bài giải:

1. Với a > 0 nhỏ tùy ý, ta chọn Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 14

Ta có: Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 15

2. Với a > 0 nhỏ tùy ý, ta chọn: 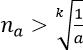Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 16

Ta có: Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 17

3. Với a > 0 nhỏ tùy ý, ta chọn: Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 18

Ta có: Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 19

Bài 5: Chứng minh các giới hạn sau:

Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 20

Bài giải:

1. Với ∀ a > 0 nhỏ tùy ý, ta chọn

Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 21
Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 22

2. Ta có:

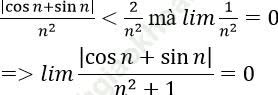
Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 23

3. Với ∀ số thực a > 0 nhỏ tùy ý, ta chọn: Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 24

Ta có: Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 25

Bài 6: Dùng định nghĩa tìm các giới hạn sau:

Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 26

Bài giải:

1. Với số thực a > 0 nhỏ tùy ý, ta chọn: Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 27

Ta có: Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 28

Vậy A = 2

2. Với số thực a > 0 nhỏ tùy ý, ta chọn na thỏa mãn: Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 29

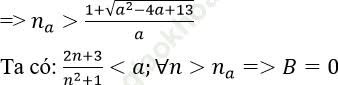
Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 30

3. Với số thực a > 0 nhỏ tùy ý, ta chọn: Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 31

Ta có: Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 32

Vậy C = 1

Bài 7: CMR: Dãy số (un): un = (-1)n không có giới hạn.

Bài giải:

Ta có: u2n → +∞; u(2n+1) = - (2n+1) → -∞

=> Dãy số đã cho không có giới hạn.

Bài 8: Chứng minh các giới hạn sau:

Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 33

Bài giải:

1. Gọi m là số tự nhiên thỏa: m+1 > |a|. Khi đó ∀ n > m+1

Ta có: Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 34

Mà: Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 35

=> Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 36

2. Nếu a = 1 => đpcm

+ Giả sử a > 1. Khi đó:

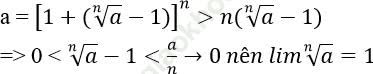
Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 37

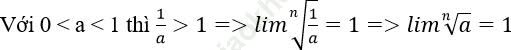
+ Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 38

=> Ta luôn có: Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 39 với a > 0.

B. Bài tập vận dụng

Bài 1: Dãy số nào sau đây có giới hạn khác 0?

Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 40

Đáp án: C

Cách 1.

Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 41
= lim⁡1 + lim (1/n) = 1 + 0 = 1

Đáp án C

Cách 2 (phương pháp loại trừ). Từ các định lí ta thấy:

Các dãy ở phương án A, B đều bằng 0, do đó loại phương án A, B

IMG_40

Do đó loại phương án D

Chọn đáp án C

Bài 2: Dãy số nào sau đây có giới hạn bằng 0?

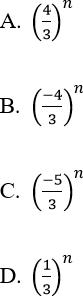
Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 42

Đáp án: D

Cách 1. Dãy (1/3)n có giới hạn 0 vì |q| < 1 thì limqn = 0. Đáp án là D

Cách 2. Các dãy ở các phương án A, B, C đều có dạng limqn nhưng |q| > 1 nên không có giưới hạn 0, do đó loại phương án A, B, C. Chọn đáp án D

Bài 3: Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 43 có giá trị bằng:

Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 44

Đáp án: D

Cách 1. Chia tử và mẫu xủa phân tử cho n (n là luỹ thừa bậc cao nhất của n trong tử và mẫu của phân thức), ta được

Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 45

Đáp án là D

Cách 2. Sử dụng nhận xét:

Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 46

khi tính limun ta thường chia tử và mẫu của phân thức cho nk (nk là luỹ thừa bậc cao nhất của n trong tử và mẫu của phân thức), từ đó được kết quả:

Nếu m < p thì limun = 0. Nếu m = p thì

Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 47

Nếu m > p thì limun = +∞ nếu am.bp > 0; limun = -∞ nếu am.bp < 0

Vì tử và mẫu của phân thức đã cho đều có bậc 1 nên kết quả

Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 48

Do đó chọn đáp án là D

Bài 4: Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 49 bằng?

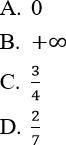
Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 50

Đáp án: A

Cách 1. Sử dụng nhận xét trên, vì bậc của tử thức nhỏ hơn bậc của mẫu thức nên kết quả

Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 51

Đáp án là A

Cách 2. Chia tử và mẫu của phân thức cho n4(n4 là luỹ thừa bậc cao nhất của n trong tử và mẫu của phân thức) rồi tính. Đáp án A

Bài 5: Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 52 bằng... ?

Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 53

Đáp án: B

Cách 1. Sử dụng nhận xét trên, vì bậc của tử thức lớn hơn bậc của mẫu thức, hệ số luỹ thừa bậc cao nhất của n cả tử và mẫu là số dương nên kết quả

Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 54

Đáp án là B

Cách 2. Chia tử và mẫu của phân thức cho n4(n4 là luỹ thừa bậc cao nhất của n trong tử và mẫu của phân thức) rồi tính. Đáp án B

Bài 6: Dãy số nào sau đây có giưới hạn bằng 1/5?

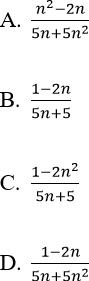
Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 55

Đáp án: A

Cách 1. Tính được

Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 56

Suy ra đáp án là A

Cách 2. . Sử dụng nhận xét trên, vì bậc của tử thức lớn hơn bậc của mẫu thức, hệ số luỹ thừa bậc cao nhất của n cả tử và mẫu thức bằng nhau và tỉ số hệ số của cúng bằng 1/5. Chỉ có dãy ở phương án A thoả mãn. Vậy đáp án là A.

Bài 7: Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 57 có giá trị bằng... ?

Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 58

Đáp án: B

Ta có:

Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 59

Đáp án B

Bài 8: Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 60 có giá trị bằng... ?

Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 61

Đáp án: A

chia cả tử thức và mẫu thức cho √ n

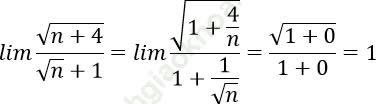
Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 62

Đáp án A

Bài 9: Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 63 bằng... ?

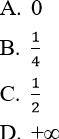
Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 64

Đáp án: B

Trước hết tính

Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 65

Do đó

Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 66

Đáp án là B

Bài 10: Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 67 bằng.... ?

Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 68

Đáp án: D

Chia cả tử thức mẫu thức cho n, ta có:

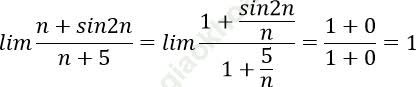
Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 69

Đáp án D

Bài 11: lim⁡ (-3n3 + 2n2 - 5) bằng... ?

A. -3

B. 0

C. -∞

D. +∞

Đáp án: C

Ta có:

Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 70

Vì

Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 71

nên lim⁡ (-3n3 + 2n2 - 5) = -∞

Đáp án C

Bài 12: Lim (2n4 + 5n2 - 7n) bằng... ?

A. -∞

B. 0

C. 2

D. +∞

Đáp án: D

Ta có:

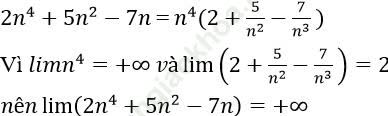
Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 72

Đáp án D

Bài 13: Dãy số nào sau đây có giưới hạn là +∞?

A. un = 9n2 - 2n5

B. un = n4 - 4n5

C. un = 4n2 - 3n

D. un = n3 - 5n4

Đáp án: C

Chỉ có dãy un = 4n2 - 3n có giới hạn là +∞, các dãy còn lại đều có giới hạn là -∞.

Đáp án C

Bài 14: Nếu limun = L, un + 9 > 0 ∀ n thì Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 73 bằng số nào sau đây?

Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 74

Đáp án: C

vì limun = L nên lim⁡ (un + 9) = L + 9 do đó

Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 75

Đáp án là C

Bài 15: Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 76 bằng:

A. 0

B. 1

C. 2

D. +∞

Đáp án: B

Cách 1. Chia tử thức và mẫu thức cho n:

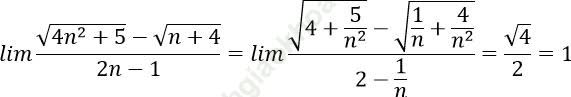
Dạng 1: Tìm giới hạn của dãy số bằng định nghĩa ảnh 77

Đáp án là B

Cách 2. Thực chất có thể coi bậc cao nhất của tử thức và mẫu thức là 1, do đó chỉ cần để ý hệ số bậc 1 của tử thức là √ 4, của mẫu thức là 2, từ đó tính được kết quả bằng 1. Đáp án B