Trang chủ > Lớp 11 > Chuyên đề Toán 11 (có đáp án) > Dạng 2: Viết phương trình tiếp tuyến khi biết hệ số góc - Chuyên đề Toán 11

Dạng 2: Viết phương trình tiếp tuyến khi biết hệ số góc - Chuyên đề Toán 11

A. Phương pháp giải & Ví dụ

- Gọi (Δ) là tiếp tuyến cần tìm có hệ số góc k.

- Giả sử M (xo; yo) là tiếp điểm. Khi đó xo thỏa mãn: f ’ (xo) = k (*)

- Giải (*) tìm xo. Suy ra yo = f (xo)

- Phương trình tiếp tuyến cần tìm là: y = k (x - xo) + yo

Lưu ý: Đối với bài toán này ta cần chú ý một số vấn đề sau:

+ Số tiếp tuyến của đồ thị chính là số nghiệm của phương trình: f’ (x) = k

+ Cho hai đường thẳng d1: y = k1x + b1 và d2: y = k2x + b2. Khi đó

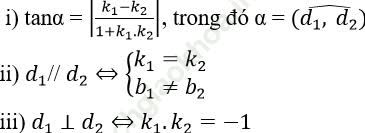
Dạng 2: Viết phương trình tiếp tuyến khi biết hệ số góc ảnh 1

Nếu đường thẳng d cắt các trục Ox, Oy lần lượt tại A, B thì tan (∠ OAB) = ± OA/OB, trong đó hệ số góc của d được xác định bởi y’ (x) = tan (∠ OAB)

Ví dụ minh họa

Bài 1: Tìm tiếp tuyến của đồ thị hàm số: Dạng 2: Viết phương trình tiếp tuyến khi biết hệ số góc ảnh 2 có hệ số góc k = -9?

Bài giải:

Tập xác định: D = R

Đạo hàm: y’ = x2 + 6x

Ta có: k = -9 ⇔ y’ (xo) = - 9

⇔ xo2 + 6xo = -9

⇔ (xo + 3)2 = 0

⇔ xo = -3 ⇒ yo = 16

Phương trình tiếp tuyến cần tìm là (d): y = -9 (x + 3) + 16 = -9x – 11

Bài 2:

1. Viết phương trình tiếp tuyến của đồ thị (C): y = - x4 – x2 + 6, biết tiếp tuyến vuông góc với đường thẳng: Dạng 2: Viết phương trình tiếp tuyến khi biết hệ số góc ảnh 3

2. Cho hàm số: Dạng 2: Viết phương trình tiếp tuyến khi biết hệ số góc ảnh 4 có đồ thị là (C). Tìm trên đồ thị (C) điểm mà tại đó tiếp tuyến của đồ thị vuông góc với đường thẳng Dạng 2: Viết phương trình tiếp tuyến khi biết hệ số góc ảnh 5.

Bài giải:

1. Hàm số đã cho xác định D = R

Gọi (t) là tiếp tuyến của đồ thị (C) của hàm số và (t) vuông góc với đường thẳng y = (1/6)x - 1, nên đường thẳng (t) có hệ số góc bằng -6

Cách 1: Gọi M (xo; yo) là tọa độ tiếp điểm của tiếp tuyến (t) và đồ thị (C) của hàm số. Khi đó, ta có phương trình:

y’ (xo) = -6 ⇔ -4xo3 - 2xo = -6

⇔ (xo - 1)(2xo2 + 2xo + 3) = 0 (*).

Vì 2xo2 + 2xo + 3 > 0 ∀ xo ∈ R nên phương trình (*) ⇔ xo = 1 ⇒ yo = 4 ⇒ M (1; 4)

Phương trình tiếp tuyến cần tìm là: y = -6 (x – 1) + 4 = -6x + 10

Cách 2: Phương trình (t) có dạng y = -6x + m

PT (t) tiếp xúc (C) tại điểm M (xo; yo) khi hệ phương trình sau có nghiệm xo

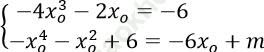
Dạng 2: Viết phương trình tiếp tuyến khi biết hệ số góc ảnh 6
⇔ Dạng 2: Viết phương trình tiếp tuyến khi biết hệ số góc ảnh 7

2. Hàm số đã cho xác định D = R

Ta có: y’ = x2 – 1

Gọi M (xo; yo) ∈ (C) ⇔ Dạng 2: Viết phương trình tiếp tuyến khi biết hệ số góc ảnh 8

Tiếp tuyến Δ tại điểm M có hệ số góc: y’ (xo) = xo2 - 1

Đường thẳng d: y = (-1/3)x + 2/3 có hệ số góc k = (-1/3)

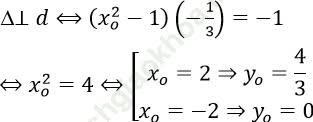
Dạng 2: Viết phương trình tiếp tuyến khi biết hệ số góc ảnh 9

Vậy có 2 điểm M (-2; 0) hoặc M = (2; 4/3) là tọa độ cần tìm.

Bài 3: Cho hàm số: Dạng 2: Viết phương trình tiếp tuyến khi biết hệ số góc ảnh 10 Viết phương trình tiếp tuyến của (C) biết tiếp tuyến vuông góc với đường thẳng y = (1/3)x + 2.

Bài giải:

TXĐ: D = R\ {1}

Ta có: Dạng 2: Viết phương trình tiếp tuyến khi biết hệ số góc ảnh 11

Gọi M (xo; yo) là tiếp điểm. Vì tiếp tuyến vuông góc với đường thẳng y = (1/3)x + 2 nên ta có:

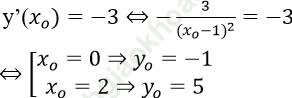
Dạng 2: Viết phương trình tiếp tuyến khi biết hệ số góc ảnh 12

+ Với M (0; -1) thì phương trình tiếp tuyến là: y = -3x – 1

+ Với M (2; 5) thì phương trình tiếp tuyến là: y = -3 (x – 2) + 5 = -3x + 11

Bài 4: Trong các tiếp tuyến tại các điểm trên đồ thị hàm số y = x3 – 3x2 + 2, tiếp tuyến có hệ số góc nhỏ nhất bằng bao nhiêu?

Bài giải:

Tập xác định: D = R

Đạo hàm: y’ = 3x2 – 6x = 3 (x-1)2 - 3 ≥ -3

Vậy trong các tiếp tuyến tại các điểm trên đồ thị hàm số đã cho, tiếp tuyến có hệ số góc nhỏ nhất bằng -3

Bài 5: Cho hàm số: Dạng 2: Viết phương trình tiếp tuyến khi biết hệ số góc ảnh 13 có đồ thị (H). Viết phương trình đường thẳng Δ vuông góc với đường thẳng d: y = - x + 2 và tiếp xúc với (H).

Bài giải:

Tập xác định: D = R\ {0}

Đạo hàm: y’ = 4/ (x2)

Đường thẳng Δ vuông góc với đường thẳng d: y = -x + 2 nên Δ có hệ số góc bằng 1. Ta có phương trình:

Dạng 2: Viết phương trình tiếp tuyến khi biết hệ số góc ảnh 14

Tại M (2; 0). Phương trình tiếp tuyến là y = 1. (x – 2) = x – 2

Tại N (-2; 4). Phương trình tiếp tuyến là y = x + 2 + 4 = x + 6

Bài 6: Lập phương trình tiếp tuyến của đường cong (C): y = x3 + 3x2 – 8x + 1, biết tiếp tuyến đó song song với đường thẳng Δ: y = x + 2017?

Bài giải:

Tập xác định: D = R

Đạo hàm: y’ = 3x2 + 6x – 8

Tiếp tuyến cần tìm song song với đường thẳng Δ: y = x + 2017 nên hệ số góc của tiếp tuyến là 1

Ta có phương trình:

Dạng 2: Viết phương trình tiếp tuyến khi biết hệ số góc ảnh 15

Tại M (1; -3). Phương trình tiếp tuyến là y = x – 1 – 3 = x – 4

Tại N (-3; 25). Phương trình tiếp tuyến là y = x + 3 + 25 = x + 28

Bài 7: Cho hàm số y = -x3 + 3x2 – 3 có đồ thị (C). Số tiếp tuyến của (C) vuông góc với đường thẳng y = (1/9)x + 2017 là bao nhiêu?

Bài giải:

Tiếp tuyến của (C) vuông góc với đường thẳng y = (1/9)x + 2017 có dạng Δ: y = -9x + c

Δ là tiếp tuyến của (C) ⇔ Hệ phương trình Dạng 2: Viết phương trình tiếp tuyến khi biết hệ số góc ảnh 16 có nghiệm

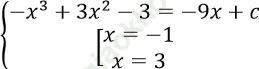
⇔ Dạng 2: Viết phương trình tiếp tuyến khi biết hệ số góc ảnh 17

Vậy có hai giá trị c thỏa mãn.

B. Bài tập vận dụng

Bài 1: Hệ số góc của tiếp tuyến của đồ thị hàm số: Dạng 2: Viết phương trình tiếp tuyến khi biết hệ số góc ảnh 18 tại giao điểm của đồ thị hàm số với trục hoành bằng:

A. 9 B. 1/9 C. -9 D. -1/9

Đáp án: A

Chọn A

Tập xác định: D = R\ {1}

Đạo hàm: y' = 1/ (x-1)2

Đồ thị hàm số cắt trục hoành tại A (2/3; 0)

Hệ số góc của tiếp tuyến là y’ (2/3) = 9

Bài 2: Hệ số góc của tiếp tuyến của đồ thị hàm số: Dạng 2: Viết phương trình tiếp tuyến khi biết hệ số góc ảnh 19 tại giao điểm với trục tung bằng:

A. -2 B. 2 C. 1 D. -1

Đáp án: B

Chọn B

Tập xác định: D = R\ {-1}

Đạo hàm: y’ = 2/ (x+1)2

Đồ thị hàm số cắt trục tung tại điểm có xo = 0 ⇒ y’ (0) = 2

Bài 3: Cho hàm số y = x3 – 3x2 có đồ thị (C) có bao nhiêu tiếp tuyến của (C) song song đường thẳng y = 9x + 10

A. 1 B. 3 C. 2 D. 4

Đáp án: C

Chọn C

Tập xác định: D = R

Đạo hàm: y’ = 3x2 – 6x. k = 9 ⇒ 3xo2 - 6xo = 9

Dạng 2: Viết phương trình tiếp tuyến khi biết hệ số góc ảnh 20

Vậy có 2 tiếp tuyến thỏa mãn yêu cầu bài toán

Bài 4: Gọi (C) là đồ thị của hàm số y = x4 + x. Tiếp tuyến của (C) vuông góc với đường thẳng d: x + 5y = 0 có phương trình là:

A. y = 5x – 3

B. y = 3x – 5

C. y = 2x – 3

D. y = x + 4

Đáp án: A

Chọn A

Ta có: y’ = 4x3 + 1

Vì tiếp tuyến vuông góc với đường thẳng y = (-1/5)x nên tiếp tuyến có hệ số góc là 5

Khi đó ta có:

4x3 + 1 = 5 ⇔ x = 1 ⇒ y = 2

Phương trình tiếp tuyến của đồ thị hàm số tại M (1; 2) có dạng

y = 5 (x – 1) + 2 = 5x – 3

Bài 5: Gọi (C) là đồ thị hàm số: Dạng 2: Viết phương trình tiếp tuyến khi biết hệ số góc ảnh 21. Tìm tọa độ các điểm trên (C) mà tiếp tuyến tại đó với (C) vuông góc với đường thẳng có phương trình y = x + 4

A. (1 + √ 3; 5+3√ 3), (1-√ 3; 5-3√ 3)

B. (2; 12)

C. (0; 0)

D. (-2; 0)

Đáp án: A

Chọn A

Tập xác định: D = R\ {1}

Đạo hàm:

Dạng 2: Viết phương trình tiếp tuyến khi biết hệ số góc ảnh 22

Giả sử a là hoành độ điểm thỏa mãn yêu cầu bài toán ⇒ y’ (a) = -1

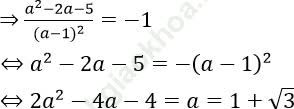
Dạng 2: Viết phương trình tiếp tuyến khi biết hệ số góc ảnh 23

Bài 6: Biết tiếp tuyến (d) của hàm số y = x3 – 2x + 2 vuông góc với đường phân giác góc phần tư thứ nhất. Phương trình (d) là:

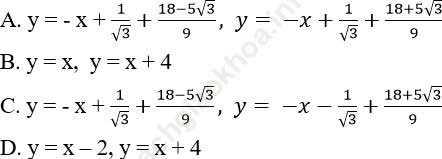
Dạng 2: Viết phương trình tiếp tuyến khi biết hệ số góc ảnh 24

Đáp án: C

Chọn C.

Tập xác định: D = R

y’ = 3x2 – 2

Đường phân giác góc phần tư thứ nhất có phương trình Δ: x = y

⇒ (d) có hệ số góc là – 1

3x2 – 2 = -1 ⇔ x = ± 1/√ 3

Phương trình tiếp tuyến cần tìm là

Dạng 2: Viết phương trình tiếp tuyến khi biết hệ số góc ảnh 25

và

Dạng 2: Viết phương trình tiếp tuyến khi biết hệ số góc ảnh 26

Bài 7: Tìm hệ số góc của tiếp tuyến với đồ thị y = tanx tại điểm có hoành độ x = π /4.

A. k = 1 B. k = 0,5 C. k = √ 2/2 D. 2

Đáp án: D

Chọn D

Dạng 2: Viết phương trình tiếp tuyến khi biết hệ số góc ảnh 27

Hệ số góc của tiếp tuyến với đồ thị y = tanx tại điểm có hoành độ x = π /4 là k = y’ (π /4) = 2

Bài 8: Hệ số góc của tiếp tuyến của đường cong: Dạng 2: Viết phương trình tiếp tuyến khi biết hệ số góc ảnh 28 tại điểm có hoành độ xo = π là:

A. -√ 3/12 B. √ 3/12 C. -1/12 D. 1/12

Đáp án: C

Chọn C

Dạng 2: Viết phương trình tiếp tuyến khi biết hệ số góc ảnh 29

Bài 9: Cho hàm số y = x3 – 6x2 + 7x + 5 (C). Tìm trên (C) những điểm có hệ số góc tiếp tuyến tại điểm đó bằng -2?

A. (-1; -9); (3; -1)

B. (1; 7); (3; -1)

C. (1; 7); (-3; -97)

D. (1; 7); (-1; -9)

Đáp án: B

Chọn B

Gọi M (xo; yo) là tọa độ tiếp điểm. Ta có y’ = 3x2 – 12x + 7

Hệ số góc của tiếp tuyến bằng -2

⇒ y’ (xo) = -2 ⇔ 3xo2 - 12xo + 7 = -2 ⇔

Dạng 2: Viết phương trình tiếp tuyến khi biết hệ số góc ảnh 30

Bài 10: Cho hàm số: Dạng 2: Viết phương trình tiếp tuyến khi biết hệ số góc ảnh 31 tiếp tuyến của đồ thị hàm số vuông góc với đường thẳng d: 3y – x + 6 = 0 là

A. y = -3x – 3; y = -3x – 11

B. y = -3x – 3; y = -3x + 11

C. y = -3x + 3; y = -3x – 11

D. y = -3x – 3; y = 3x – 11

Đáp án: A

Chọn A

d: 3y – x + 6 = 0 ⇔ y = (1/3)x - 2

Gọi M (xo; yo) là tọa độ tiếp điểm. Ta có

Dạng 2: Viết phương trình tiếp tuyến khi biết hệ số góc ảnh 32

Tiếp tuyến vuông góc với d nên hệ số góc của tiếp tuyến là -3 nên y’ (xo) = -3

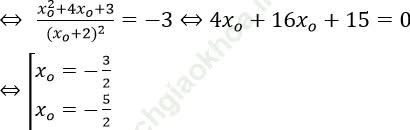
Dạng 2: Viết phương trình tiếp tuyến khi biết hệ số góc ảnh 33

Với xo = -3/2 ⇒ yo = 3/2 ⇒ phương trình tiếp tuyến: y = -3 (x + 3/2) + 3/2 = -3x-3

Với xo = -5/2 ⇒ yo = (-7)/2 ⇒ phương trình tiếp tuyến: y = -3 (x + 5/2)-7/2 = -3x-11

Bài 11: Tìm m để tiếp tuyến của đồ thị hàm số y = (2m – 1)x4 – m + 5/4 tại điểm có hoành độ x = - 1 vuông góc với đường thẳng d: y = 2x – y – 3 = 0

A. 3/4 B. 1/4 C. 7/16 D. 9/16

Đáp án: D

Chọn D

d: y = 2x – y – 3 = 0 ⇔ y = 2x – 3, hệ số góc của đường thẳng d là 2

y’ = 4 (2m – 1)x3

Hệ số góc của tiếp tuyến với đồ thị hàm số y = (2m – 1)x4 – m + 5/4 tại điểm có hoành độ x = -1 là y’ (-1) = -4 (2m – 1)

Ta có 2. -4 (2m – 1) = -1 ⇔ m = 9/16

Bài 12: Cho hàm số: Dạng 2: Viết phương trình tiếp tuyến khi biết hệ số góc ảnh 34 có đồ thị cắt trục tung tại A (0; -1), tiếp tuyến tại A có hệ số góc k = -3. Các giá trị của a, b là

A. a = 1, b = 1

B. a = 2, b = 1

C. a = 1, b = 2

D. a = 2, b = 2

Đáp án: B

Chọn B

A (0; - 1) ∈ (C) nên ta có: -1 = b/ (-1) ⇔ b = 1

Ta có

Dạng 2: Viết phương trình tiếp tuyến khi biết hệ số góc ảnh 35
Hệ số góc của tiếp tuyến với đồ thị tại điểm A là:

k = y’ (0) = -a – b = -3 ⇔ a = 3 – b = 2.

Bài 13: Điểm M trên đồ thị hàm số y = x3 - 3x2 - 1 mà tiếp tuyến tại đó có hệ số góc k bé nhất trong tất cả các tiếp tuyến của đồ thị thì M, k là

A. M (1; -3), k = -3

B. M (1; 3), k = -3

C. M (1; -3), k = 3

D. M (-1; -3), k = -3

Đáp án: A

Chọn A.

Gọi M (xo; yo). Ta có y’ = 3x2 – 6x

Hệ số góc của tiếp tuyến với đồ thị tại M là:

k = y’ (xo) = 3xo2 - 6xo = 3 (xo - 1)2 - 3 ≥ -3

Vậy k bé nhất bằng -3 khi xo = 1, yo = -3

Bài 14: Cho hàm số y = x3 + 3x2 - 6x + 1 (C). Viết phương trình tiếp tuyến của đồ thị (C) biết tiếp tuyến vuông góc với đường thẳng y = (-1/18)x + 1

A. y = 18x + 8 và y = 18x -27

B. y = 18x + 8 và y = 18x - 2

C. y = 18x + 81 và y = 18x - 2

D. y = 18x + 81 và y = 18x - 27

Đáp án: D

Chọn D.

Gọi M (xo; yo) là tiếp điểm

Ta có: y’ = 3x2 + 6x – 6

Vì tiếp tuyến vuông góc với đường thẳng y = (-1/18)x + 1 nên ta có:

y' (xo) = 18 ⇔ 3xo2 + 6xo - 6 = 18 ⇔

Từ đó ta tìm được hai tiếp tuyến: y = 18x + 81 và y = 18x – 27

Bài 15: Cho hàm số y = x3 - 3x + 1 (C). Viết phương trình tiếp tuyến của đồ thị (C), biết hệ số góc của tiếp tuyến bằng 9

A. y = 9x - 1 hay y = 9x + 17

B. y = 9x - 1 hay y = 9x + 1

C. y = 9x - 13 hay y = 9x + 1

D. y = 9x - 15 hay y = 9x + 17

Đáp án: D

Chọn D

Ta có: y’ = 3x2 – 3. Gọi M (xo; yo) là tiếp điểm

Ta có: y’ (xo) = 9 ⇔ 3xo2 - 3 = 9 ⇔ xo = ±2

xo = 2 ⇒ yo = 3. Phương trình tiếp tuyến: y = 9 (x – 2) + 3 = 9x – 15

xo = -2 ⇒ yo = -1. Phương trình tiếp tuyến: y = 9 (x + 2) – 1 = 9x + 17