Tìm điều kiện để dãy số lập thành cấp số cộng cực hay - Chuyên đề Toán 11

A. Phương pháp giải

+ Điều kiện để ba số a; b; c lập thành cấp số cộng là: c − b = b − a hay a + c= 2b.

+ Điều kiện để dãy số (u_n) là cấp số cộng là với ∀ n ∈ N* thì: u_n+1 − u_n là hằng số (không phụ thuộc vào n).

B. Ví dụ minh họa

Ví dụ 1: Xác định x để 3 số: 1 − x; x²; 1 + x theo thứ tự lập thành một cấp số cộng?

A. Không có giá trị nào của x.

B. x = ± 2.

C. x = ± 1.

D. x = 0

Bài giải:

Ba số: 1 − x; x²; 1 + x lập thành một cấp số cộng khi và chỉ khi:

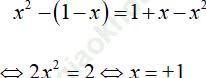
Đáp án đúng là: C.

Ví dụ 2: Xác định n để ba số 2n - 9; n; n + 3 theo thứ tự lập thành cấp số cộng?

A. n = 2

B. n = 3

C. n= 4

D. n= 5

Bài giải:

Điều kiện để ba số: 2n – 9; n và n+ 3 theo thứ tự lập thành cấp số cộng là:

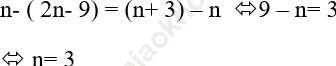
Đáp án đúng là: B.

Ví dụ 3: Xác định x để 3 số: 1 + 2x; 2x² − 1; − 2x theo thứ tự lập thành một cấp số cộng?

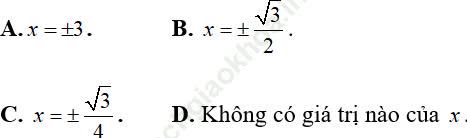
Bài giải:

Ba số 1 + 2x; 2x² − 1; − 2x theo thứ tự lập thành một cấp số cộng khi và chỉ khi

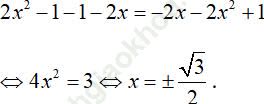
Đáp án đúng là: B.

Ví dụ 4: Xác định a để 3 số 2 - a; 6 + a2; 3a + 2 theo thứ tự lập thành một cấp số cộng?

A. Không có giá trị nào của.

B. a= 4

C. a= ± 2

D. a= ± √ 5

Bài giải:

Ba số 2 - a; 6 + a2; 3a + 2 theo thứ tự lập thành một cấp số cộng khi và chỉ khi:

6 + a² − 2 + a = 3a + 2 - 6 - a²

⇔ 2a² − 2a + 8 = 0 phương trình này vô nghiệm.

=> Không có giá trị nào của a thỏa mãn.

Đáp án đúng là: A.

Ví dụ 5: Cho tam giác ABC biết 3 góc của tam giác lập thành một cấp số cộng và có một góc bằng 25⁰. Tìm 2 góc còn lại?

A. 65^o; 90^o.

B. 75^o; 80^o.

C. 60^o; 95^o.

D. 60^o; 90^o.

Bài giải:

Gọi 3 góc của tam giác là u₁ = 25; u₂ = 25 + d và u₃ = 25 + 2d.

Tổng 3 góc trong một tam giác bằng 180⁰ nên ta có:

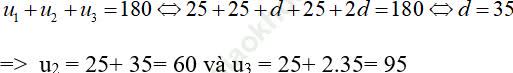
Vậy hai góc còn lại của tam giác là 60⁰ và 95⁰

Đáp án đúng là: C.

Ví dụ 6: Cho tứ giác ABCD biết 4 góc của tứ giác lập thành một cấp số cộng và góc Acó số đo nhỏ nhất và bằng 30^o. Tìm tổng của góc lớn nhất và góc nhỏ nhất của tứ giác.

A. 180^o

B. 150^o.

C. 200^o.

D. 210^o.

Bài giải:

Do 4 góc của tứ giác lập thành cấp số cộng và nên các góc còn lại của tứ giác là:

u₂ = 30 + d; u₃ = 30 + 2d và u₄ = 30 + 3d

Do tổng bốn góc của 1 tứ giác là 360⁰ nên:

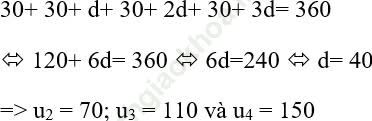
Vậy các góc còn lại của tứ giác là: 70⁰; 110⁰ và 150⁰

=> Góc lớn nhất và góc nhỏ nhất của tứ giác là 150⁰ và 30⁰

Đáp án đúng là: A.

Ví dụ 7: Tìm bốn số hạng liên tiếp của một cấp số cộng biết tổng của chúng bằng 20 và tổng các bình phương của chúng bằng 120.

A. 1,5,6,8

B. 2,4,6,8

C. 1,4,6,9

D. 1,4,7,8

Bài giải:

Giả sử 4 số hạng liên tiếp cần tìm là: a- 3d; a- d; a+ d; a+ 3d với công sai là d’= 2d. Khi đó, ta có:

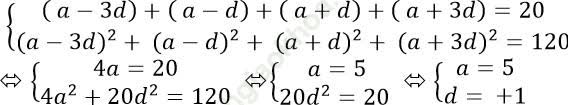
+ Nếu d = 1 thì bốn số cần tìm là: 2; 4; 6; 8

+ Nếu d = − 1 thì bốn số cần tìm là: 8; 6; 4; 2

Đáp án đúng là: B.

Lưu ý:

* Cách gọi các số hạng của cấp số cộng như trên giúp ta giải quyết bài toán gọn hơn.

* Nếu số hạng cấp số cộng là lẻ thì gọi công sai, là chẵn thì gọi công sai rồi viết các số hạng cấp số dưới dạng đối xứng.

Ví dụ 8: Biết 3 số: x² + 1; x − 2 và 1 − 3x theo thứ tự lập thành cấp số cộng. Hỏi có mấy giá trị nguyên dương của x thỏa mãn?

A. 0

B. 1

C. 2

D. 3

Bài giải:

Ta có: x² + 1; x − 2; 1 − 3x theo thứ tự lập thành cấp số cộng nên:

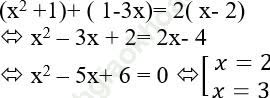
Vậy có hai giá trị nguyên dương của x thỏa mãn đầu bài.

Đáp án đúng là: C.

Ví dụ 9: Xác định a; b để phương trình x³ + ax + b = 0 có ba nghiệm phân biệt lập thành cấp số cộng.

A. b = 0; a < 0

B. b = 0; a = 1

C. b = 0; a > 0

D. b > 0; a < 0

Bài giải:

Giả sử phương trình đã cho có 3 nghiệm phân biệt là x₁; x₂ và x₃

* Do 3 số này lập thành cấp số cộng nên x₁ + x₃ = 2x₂ (1)

* Áp dụng hệ thức vi- et cho phương trình bậc 3 ta có:

x₁ + x₂ + x₃ = 0 (2)

Từ (1) và (2) suy ra: 2x₂ + x₂ = 0 ⇔ x₂ = 0

Suy ra phương trình đã cho có nghiệm x = 0. Thay x = 0 vào phương trình đã cho ta được: 0³ + a. 0 + b = 0 ⇔ b = 0.

* Với b = 0 phương trình đã cho trở thành: x³ + ax = 0

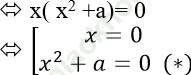
Do đó, để phương trình đã cho có 3 nghiệm phân biệt khi và chỉ khi (*) có hai nghiệm phân biệt khác 0 khi và chỉ khi: a < 0.

Vậy điều kiện để phương trình đã cho có 3 nghiệm phân biệt lập thành cấp số cộng là:

b = 0 và a < 0.

Đáp án đúng là: A.

Ví dụ 10: Tìm m để phương trình mx⁴ − 2 (m − 1)x² + m − 1= 0 có bốn nghiệm phân biệt lập thành cấp số cộng.

Bài giải:

Đặt x² = t (t ≥ 0) khi đó phương trình đã cho trở thành:

mt² − 2 (m − 1)t + m − 1 = 0 (*)

Để phương trình đã cho có 4 nghiệm phân biệt khi và chỉ khi phương trình (*) có 2 nghiệm dương phân biệt 0 < t₁ < t₂

Khi đó phương trình đã cho có 4 nghiệm phân biệt là − √ t₂; − √ t₁; √ t₁; √ t₂

Để 4 nghiệm này lập thành cấp số cộng thì:

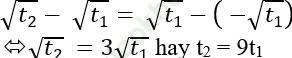
Áp dụng hệ thức Vi-et với phương trình (*) ta có:

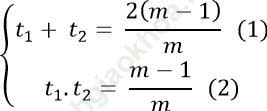
Thay t₂ = 9t₁ vào (1) ta được:

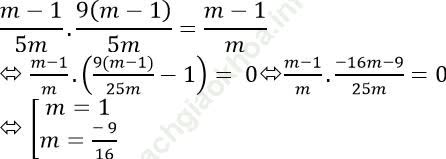
Thử lại: Thay vào phương trình đã cho ta thấy thỏa mãn.

Đáp án đúng là: B.

C. Bài tập trắc nghiệm

Câu 1: Với giá trị nào của x để ba số: 10 − 3x; 2x² + 3 và 7 − 4x theo thứ tự lập thành cấp số cộng?

Hiển thị đáp án

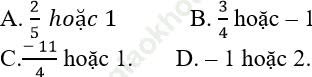
Đáp án: C

Để ba số 10 − 3x; 2x² + 3 và 7 − 4x theo thứ tự lập thành cấp số cộng khi:

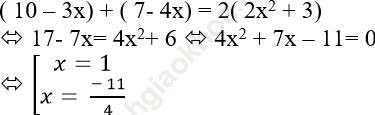
Câu 2: Một tam giác vuông có chu vi bằng 3a và 3 cạnh lập thành cấp số cộng. Tính diện tích tam giác vuông đó theo a.

Hiển thị đáp án

Đáp án: B

Gọi x, y, z theo thứ tự tăng dần của độ dài ba cạnh của tam giác.

Chu vi của tam giác: x + y + z = 3a (1)

Tính chất của cấp số cộng có x + z = 2y (2)

Vì tam giác vuông nên có: x² + y² = z² (3)

Thay (2) vào (1) được 3y = 3a ⇔ y = a thay y = a vào (2) được:

x + z = 2a ⇔ x = 2a − z

Thay x và y vào (3) được: (2a- z)² + a² = z²

Vậy độ dài ba cạnh của tam giác cần tìm là:

=> Diện tích tam giác vuông này là:

Câu 3: Biết rằng 3 số hạng liên tiếp của 1 cấp số cộng biết tổng của chúng bằng 27 và tổng các bình phương của chúng là 293. Hỏi số lớn nhất trong 3 số đó bằng bao nhiêu?

A. 14

B. 9

C. 11

D. 13

Hiển thị đáp án

Đáp án: A

Gọi 3 số hạng liên tiếp của cấp số cộng u₁ − d; u₁; u₁ + d. Theo đề bài ta có:

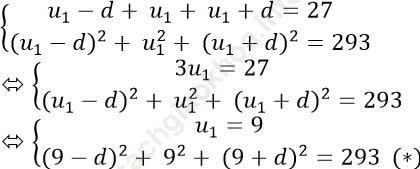
Giải phương trình (*):

+ Với d = 5=> Ba số hạng cần tìm là: 4; 9; 14.

+ Với d = − 5 => Ba số hang cần tìm là: 14; 9; 4

Câu 4: Biết rằng 4 số hạng liên tiếp của một cấp số cộng có tổng bằng 20 và tích của của chúng là 384. Tìm số bé nhất trong bốn số đó.

A. 2

B. 5 − √ 241

C. − √ 241

D. Đáp án khác

Hiển thị đáp án

Đáp án: D

Gọi 4 số hạng của cấp số cộng cần tìm là u₁ = u − 3d; u₂ = u − d; u₃ = u + d và u₄ = u + 3d có công sai d' = 2d.

Theo đề bài ta có:

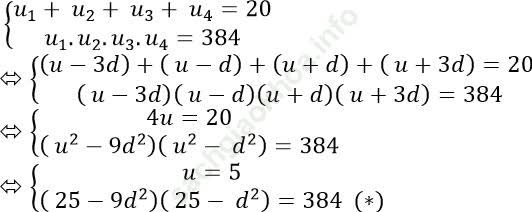
Đặt t = d² (t ≥ 0); khi đó phương trình (*) trở thành:

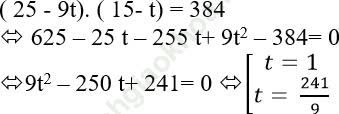
* Với t = 1 => d² = 1 ⇔ d = ± 1

Với d = 1 => u₁ = 2; u₂ =4; u₃ = 6 và u₄ = 8

Với d = − 1 => u₁ = 8; u₂ = 6; u₃ =4 và u₄ = 2

* Với:

Với

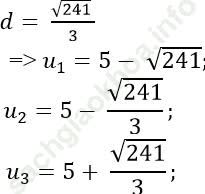
và u₄ = 5 + √ 241

Với

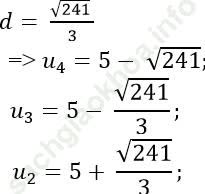
và u₁ = 5 + √ 241

Câu 5: Xác định m để phương trình x³ − 3x² − 9x + m = 0 có ba nghiệm phân biệt lập thành cấp số cộng.

A. m = 16

B. m = 11

C. m = 13

D. m = 12

Hiển thị đáp án

Đáp án: B

Giả sử phương trình có ba nghiệm phân biệt x1; x2; x3 lập thành cấp số cộng.

=> x₁ + x₃ = 2x₂

Theo hệ thức Viet cho phương trình bậc ba ta có:

=> 3x₂ = 3 ⇔ x₂ = 1

Thay x= 1 vào phương trình đã cho ta được:

1³ − 3.12 − 9.1 + m = 0 ⇔ m = 11

Với m = 11 ta có phương trình x³ − 3x² − 9x + 11 = 0

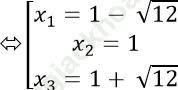
Ba nghiệm này lập thành cấp số cộng.

Vậy m = 11 là giá trị cần tìm.

Câu 6: Tìm m để phương trình x⁴ − 2 (m + 1).x² + 2m + 1 = 0 (1) có bốn nghiệm phân biệt lập thành cấp số cộng.

A. m = 16

B. m = 11

C. m = 13

D. m = 12

Hiển thị đáp án

Đáp án: B

Đặt t = x² (t ≥ 0).

Phương trình trở thành: t² − 2 (m+1)t + 2m + 1 = 0 (2)

Phương trình (1) có bốn nghiệm phân biệt khi và chỉ khi phương trình (2) có hai nghiệm dương phân biệt 0 < t₁ < t₂

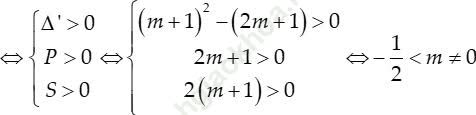
Với điều kiện trên phương trình (2) có bốn nghiệm là:

Bốn nghiệm này lập thành cấp số cộng khi:

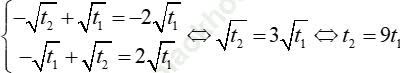
Theo định lý viet thì

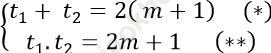
Thay t₂ = 9t₁ vào (*) ta được:

thay vào (**) ta được:

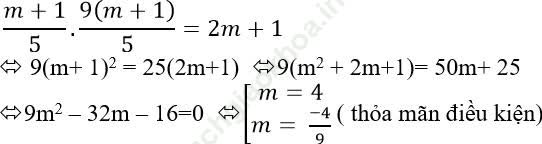
Vậy m = 4 hoặc

là những giá trị cần tìm.

Câu 7: Cho tam giác ABC có độ dài các cạnh là a, b, c theo thứ tự lập thành một cấp số cộng. Biết 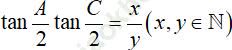, giá trị x + y là:

A. 4

B. 1

C. 2

D. 3

Hiển thị đáp án

Đáp án: A

Ta có:

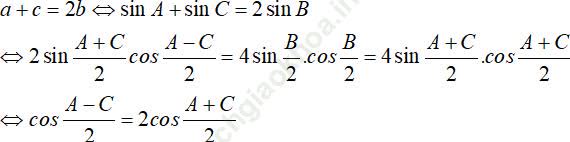
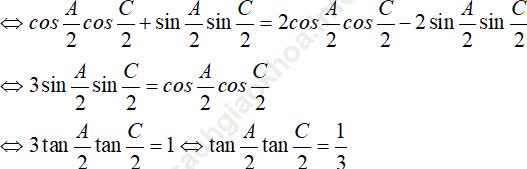
Do đó x + y = 4

Câu 8: Có bao nhiêu giá trị của tham số m để phương trình x³ − (3m + 1).x² + 2mx = 0 có ba nghiệm phân biệt lập thành một cấp số cộng.

A. 0

B. 1

C. 2

D. 3

Hiển thị đáp án

Đáp án: D

Ta có:

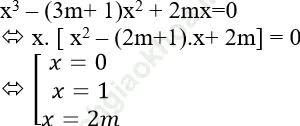
Để phương trình đã cho có ba nghiệm phân biệt

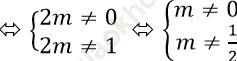
● Để các nghiệm này lập thành cấp số cộng nên ta sắp xếp các nghiệm này theo thứ tự tăng dần được các dãy số sau:

+ 2m, 0,1 lập thành cấp số cộng

+ 0,2m, 1 lập thành cấp số cộng

+ 0,1,2m lập thành cấp số cộng

Vậy có ba giá trị của m thỏa mãn là:

là các giá trị cần tìm.

Câu 9: Tìm m để phương trình: x³ − 3x² − 9x + m = 0 có ba nghiệm phâ biệt và các nghiệm đố theo thứ tự lập thành cấp số cộng.

A. m = 11

B. m = 12

C. m = -11

D. m = 18

Hiển thị đáp án

Đáp án: A

* Điều kiện cần:

Ta có: x³ − 3x² − 9x + m = 0 (*)

Gọi x₁ < x₂ < x₃ là ba nghiệm của phương trình (*). Khi đó, ta sẽ phân tích được:

Đồng nhất hệ số của x₂ ta được: x₁ + x₂ + x₃ = 3 (1).

Do x₁; x₂; x₃ lập thành một cấp số cộng theo thứ tự đó nên x₁ + x₃ = 2x₂ (2).

Thế (2) vào (1) ta được: 3x₂ = 3 ⇔ x₂ = 1.

Thế x₂ = 1 vào (*) được m = 11.

* Điều kiện đủ.

Thay m = 11 vào phương trình đã cho ta được:

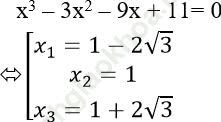
Vậy m = 11 là giá trị cần tìm.

Bài trước: Cách tính tổng n số hạng đầu tiên của cấp số cộng cực hay có lời giải - Chuyên đề Toán 11 Bài tiếp: Cách chứng minh đẳng thức dựa vào tính chất của cấp số cộng cực hay - Chuyên đề Toán 11