Cách chứng minh một dãy số là cấp số nhân cực hay có lời giải - Chuyên đề Toán 11

A. Phương pháp giải

Cách 1. Chứng minh ∀ n ≥ 1; u_n+1 = u_n q. Trong đó, q là một số không đổi.

Cách 2. Nếu u_n ≠ 0 với mọi n thì ta lập tỉ số

T là hằng số thì (u_n) là cấp số nhân có công bội q = T.

T phụ thuộc vào n thì (u_n) không là cấp số nhân.

Cách 3. Chỉ ra tồn tại số k ≥ 2 sao cho:

B. Ví dụ minh họa

Ví dụ 1: Cho dãy số (u_n) xác định bởi: u_n = 2²ⁿ⁺¹. Chứng minh (u_n) là cấp số nhân

Bài giải:

Ta có:

Xét tỉ số:

=> Dãy số (u_n) là cấp số nhân với công bội q = 4.

Ví dụ 2: Cho dãy số (u_n) xác định bởi: u_n = (-1)ⁿ. (-3)ⁿ⁺¹. Chứng minh (u_n) là cấp số nhân.

Bài giải:

Ta có:

Xét tỉ số:

=> Dãy số (u_n) là cấp số nhân với công bội q = 3.

Ví dụ 3: Cho dãy số (u_n) xác định bởi: . Chứng minh dãy số (u_n) không phải là cấp số nhân.

Bài giải:

Ta có:

Xét tỉ số:

=> Dãy số (u_n) không là cấp số nhân.

Ví dụ 4: Cho dãy số (u_n) xác định bởi u_n = 2n + 10. Chứng minh dãy số (u_n) không là cấp số nhân.

Bài giải:

Ta có: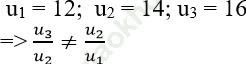

=> dãy số (u_n) không là cấp số nhân.

Ví dụ 5: Cho dãy số (u_n) xác định bởi 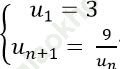. Chứng minh rằng dãy số (u_n) là cấp số nhân?

Bài giải:

* Ta có: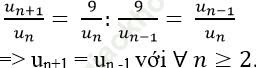

* Do đó có: u₁ = u₃ = u₅ =... = u_{2n+ 1} =... (1)

Và u₂ = u₄ = u₆ =... = u_2n =... (2)

Theo đề bài có:

Từ (1), (2), (3) suy ra u₁ = u₂ = u₃ =... = u_2n = u_{2n+ 1} =....

Kết luận (u_n) là cấp số nhân với công bội q = 1.

Ví dụ 6: Cho dãy số (u_n) được xác định bởi u_n = 30. Chứng minh rằng (u_n) là cấp số nhân.

Bài giải:

Ta có: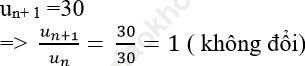

=> (u_n) là cấp số nhân với q = 1.

Ví dụ 7: Cho dãy số (u_n) xác định bởi . Chứng minh dãy số (u_n) là cấp số nhân.

Bài giải:

Ta có:

Xét tỉ số:

=> dãy số (u_n) là cấp số nhân với

C. Bài tập trắc nghiệm

Câu 1: Cho dãy số (u_n): . Chứng minh dãy số (u_n) là cấp số nhân.

Hiển thị đáp án

Ta có:

Và

=> dãy số trên là cấp số nhân với

Câu 2: Cho dãy số (u_n) xác định bởi: . Chứng minh dãy số (u_n) là cấp số nhân.

Hiển thị đáp án

Ta có:

Xét tỉ số

=> (u_n) là cấp số nhân.

Câu 3: Cho dãy số (u_n) xác định bởi: u_n = 10n + 10. Chứng minh dãy số (u_n) không là cấp số nhân.

Hiển thị đáp án

Ta có:

Xét tỉ số:

phụ thuộc vào n.

=> Dãy số (u_n) không là cấp số nhân.

Câu 4: Cho dãy số (u_n) xác định bởi . Chứng minh (u_n) là cấp số nhân.

Hiển thị đáp án

Ta có:

Xét tỉ số:

=> (u_n) là cấp số nhân.

Câu 5: Cho dãy số (u_n) xác định bởi: u_n= n. 2n. Chứng minh dãy số (u_n) không là cấp số nhân.

Hiển thị đáp án

Ta có;

Xét tỉ số:

=> Dãy số (u_n) không là cấp số nhân.

Câu 6: Cho dãy số (u_n) được xác định bởi 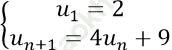. Đặt vn= u_n + 3. Chứng minh (vn) là cấp số nhân.

Hiển thị đáp án

Ta có: v_n = u_n+ 3 (1) nên v_n+1 = u_n+1 + 3 (2).

Theo đề bài: u_n+1 = 4u_n + 9 => u_n+1 + 3 = 4u_n + 9 + 3 = 4 (u_n + 3) (3)

Thay (1) và (2) vào (3) được: v_n+1 = 4v_n ∀ n ≥ 1

Kết luận (v_n) là cấp số nhân với công bội q = 4 và số hạng đầu v₁ = u₁ + 3 = 5.

Câu 7: Cho dãy số (u_n) xác định bởi . Chứng minhh rằng dãy số (u_n) không là cấp số nhân.

Hiển thị đáp án

Ta có:

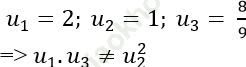
Suy ra dãy số (u_n) đã cho không là cấp số nhân.

Bài tiếp: Cách tìm số hạng đầu tiên, công bội, số hạng thứ k của cấp số nhân cực hay - Chuyên đề Toán 11