Phương trình đối xứng, phản đối xứng đối với sinx và cosx - Chuyên đề Toán 11
A. Phương pháp giải
+ Phương trình đối xứng đối với sinx và cosx có dạng:
a (sinx+ cosx)+ b. sinx. cosx + c = 0
Để giải phương trình này ta làm như sau:
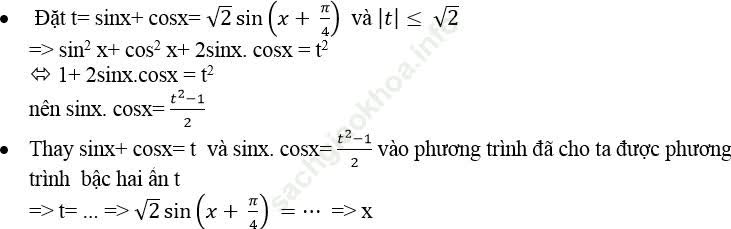
+ Phương trình phản đối xứng đối với sinx và cosx có dạng:
a (sinx- cosx)+ b. sinx. cosx + c = 0
Để giải phương trình này ta làm như sau:

B. Ví dụ minh họa
Ví dụ 1. Phương trình: ![]() có nghiệm là:
có nghiệm là:
A. 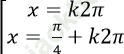
B. 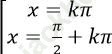
C. 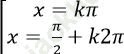
D. 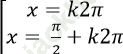
Bài giải:
Đáp án đúng là: D
Hướng dẫn:
Đặt sinx + cosx = t (|t| ≤ √ 2)
⇒ sin 2 x+ cos2 x + 2sinx. cosx = t2
⇒ 1+ sin2x = t2
⇒ sin2x = t2 – 1
Thay vào phương trình đã cho ta được:
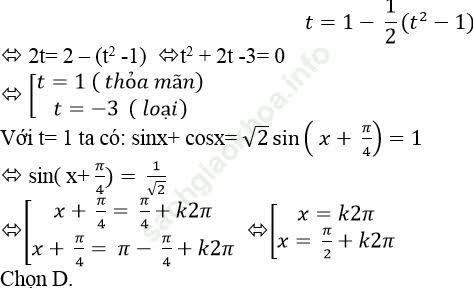
Ví dụ 2. Phương trình: ![]() có nghiệm là:
có nghiệm là:
A. 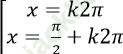
B. 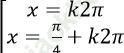
C.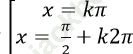
D. Đáp án khác
Bài giải:
Đáp án đúng là: A.
Hướng dẫn:
Ta có: sin3 x+ cos3 x= 1- 1/2. sin2x
⇒ (sinx+ cosx). (sin2 x- sinx. cosx + cos2 x) = 1- 1/2.2sinx. cosx
⇒ (sinx+ cosx). (1- sinx. cosx) = 1- sinx. cosx
⇒ (sinx+ cosx). (1- sinx. cosx) – (1 – sinx. cosx) = 0
⇒ (sinx+ cosx – 1). (1 – sinx. cosx) = 0
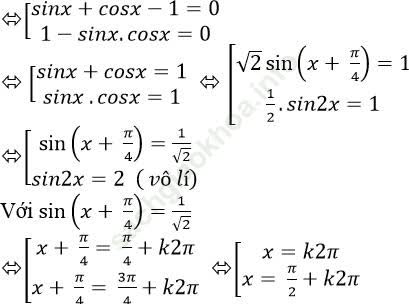
Ví dụ 3: Phương trình sinx + cosx – 4. sinx. cosx – 1= 0 có bao nhiêu họ nghiệm
A. 2
B. 1
C. 3
D. 4
Bài giải:
Đáp án đúng là: D.
Hướng dẫn:
Ta có: sinx + cosx – 4sinx. cosx – 1 = 0

Ví dụ 4: Giải phương trình sin2x – 12 (sinx - cosx) + 12 = 0
A. 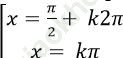
B. 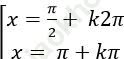
C. 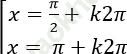
D. Tất cả sai
Bài giải:
Đáp án đúng: C.
Hướng dẫn:
Đặt t = sinx - cosx = √ 2 sin (x - π/4) với |t| ≤ √ 2
⇒ sin2 x + cos2 x - 2sinx. cosx = t2
⇒ 1 - sin2x = t2
⇒ sin2x = 1 - t2
Thay vào phương trình đã cho ta được: 1 - t2 - 12. t + 12 = 0
⇒ - t2 – 12t + 13 = 0
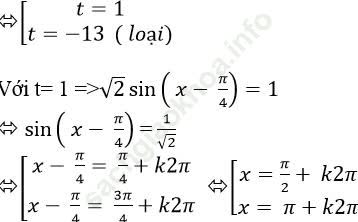
Ví dụ 5: Giải phương trình ![]()
A. ![]()
B. ![]()
C. ![]()
D. Đáp án khác
Bài giải:
Đáp án đúng là: C.
Hướng dẫn:
Đặt t = sinx - cosx = √ 2sin (x - π/4) với |t| ≤ √ 2
⇒ sin2 x + cos2 x – 2sinx. cosx = t2
⇒ 1 – 2sinx. cosx = t2
⇒ 2sinx. cosx = 1 - t2

Ví dụ 6. Giải phương trình: ![]()
A. ![]()
B. ![]()
C. ![]()
D. Đáp án khác
Bài giải:
Đáp án đúng là: A.
Hướng dẫn:
+ Điều kiện: sinx ≠ 0

Ví dụ 7. Giải phương trình |sinx-cosx| + 4. sinx. cosx - 1 = 0
A. x = kπ/2
B. x = kπ
C. x = π/2 + kπ
D. x = k2π
Bài giải:
Đặt t = |sinx - cosx| = √ 2 |sin (x - π/4) | (0 ≤ t ≤ √ 2)
⇒ sin2 x + cos2 x – 2sinx. cosx = t2
⇒ 1 – 2sinx. cosx = t2
⇒ 2sinx. cosx = 1 - t2
Khi đó: Ta có: t+ 2 (1 - t2) – 1 = 0
⇒ - 2t2 + t + 1 = 0

Ví dụ 8: Giải phương trình cos3 x + sin3 x = cos2 x - sin2x
A. 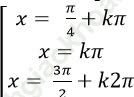
B. 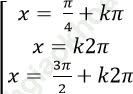
C. 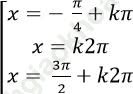
D. Đáp án khác
Bài giải:
Đáp án đúng là: C.
Hướng dẫn:
Ta có: cos3 x + sin3 x = cos2 x - sin2x
⇒ (cosx + sinx). (cos2 x – cosx. sinx + sin2 x) = (cosx - sinx). (cosx + sinx)
⇒ (cosx + sinx). (1 - cos x. sinx) – (cosx - sinx). (cosx + sinx) = 0
⇒ (cosx + sinx). (1 - cosx. sinx – cosx + sinx) = 0
⇒ (cosx + sinx). [( 1 - cosx) + (sinx - cosx. sinx)] = 0
⇒ (cosx + sinx). [(1 - cosx) + sinx (1 - cos)] = 0
⇒ (cosx + sinx). (1 - cosx). (1 + sinx) = 0
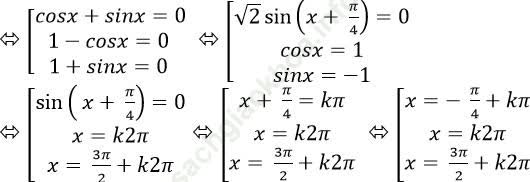
Ví dụ 9: Giải phương trình sin3 x – cosx + cos3 x - sinx = 2sin2x
A. x = kπ
B. x = kπ/2
C. x = kπ/4
D. Đáp án khác
Bài giải:
Đáp án đúng: B.
Hướng dẫn:
Ta có: sin3 x – cosx + cos3 x - sinx = 2sin2x
⇒ (sin3 x+ cos3 x) - (cosx + sinx) - 2sin2x = 0
⇒ (sinx + cosx). (sin2 x - sinx. cosx + cos2 x) – (cosx + sinx) – 2sin2x = 0
⇒ (sinx + cosx). (1 - sinx. cosx) – (cosx + sinx) – 2.2. sinx. cosx = 0
⇒ (sinx + cosx). (1 - sinx. cosx - 1) – 4. sinx. cosx = 0
⇒ - (sinx + cosx). sinx. cosx – 4. sinx. cosx = 0 (*)
⇒ - sinx. cosx [sinx + cosx + 4] = 0
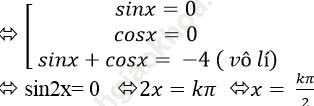
C. Bài tập vận dụng
Câu 1: Giải phương trình: ![]()
A. x=+kπ
B. ![]()
C. ![]()
D. ![]()
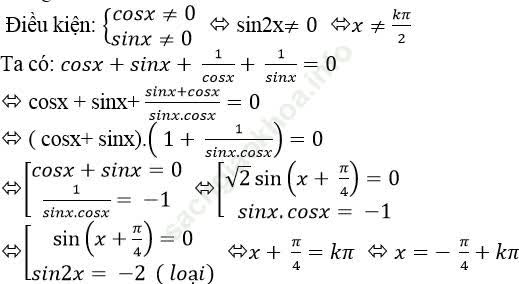
Chọn D.
Câu 2:Cho phương trình sinx. cosx – sinx- cosx + m= 0 trong đó m là tham số thực. Để phương trình có nghiệm, các giá trị thích hợp của m là... ?
A. -√ 2-1/2 ≤ m ≤ 1
B. √ 2-1/2 ≤ m ≤ 1
C. -√ 2-1/2 < m < 1
D. Đáp án khác

Chọn A.
Câu 2: Phương trình 2sin2x-3√ 6 |sinx+cosx|+8=0 có nghiệm là
A. 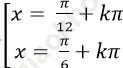
B. 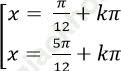
C. 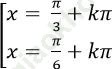
D. Đáp án khác
Đặt t= |sinx+cosx|= √ 2|sin (x+ π/4)|; 0 ≤ t ≤ √ 2
⇒ sin2 x+ cos2 x+ 2sinx. cosx = t2
⇒ 1 + 2sinx. cosx= t2 nên 2sinx. cosx= t2 -1
Khi đó; phương trình đã cho trở thành:
2 (t2 -1)-3√ 6. t+8=0
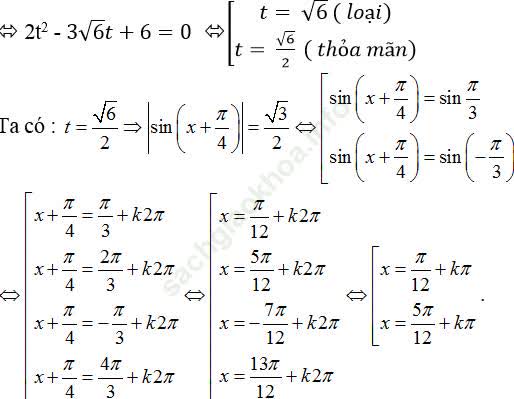
Câu 3: Giải phương trình sinx. cosx + 2 (sinx + cosx) = 2.
A. 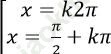
B. 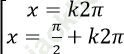
C. 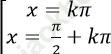
D. 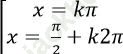
Đặt t= sinx+ cosx = √ 2sin (x+ π/4) với |t| ≤ √ 2
⇒ t2 = sin2 x+ cos2 x + 2sinx. cosx
⇒ t2 = 1+ 2sinx. cosx ⇒ sinx. cosx=
Khi đó, phương trình đã cho trở thành:
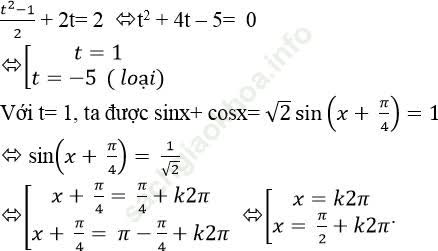
Câu 4: Cho phương trình 5sin2x + sinx + cosx + 6 = 0. Trong các phương trình sau, phương trình nào tương đương với phương trình đã cho?
A. sin x = 1/2
B. cosx = 1
C. cot x = 1
D. 1 + sin2x = 0
Đặt t= sinx+ cosx = √ 2 sin (x+π/4) với |t| ≤ √ 2
⇒ t2 = sin2 x+ cos2 x+ 2. sinx. cosx
⇒ t2 =1+ 2sinx. cosx ⇒ sin2x= 2sinx. cosx = t2 – 1
Khi đó, phương trình đã cho trở thành:
5. (t2 -1) + t+ 6= 0
⇒ 5t2 + t + 1= 0 phương trình này vô nghiệm
Ta thấy trong các phương án A, B, C, D thì phương trình ở đáp án D vô nghiệm.
Vậy phương trình đã cho tương đương với phương trình 1+sin2 x=0
( chú ý: Hai phương trình được gọi là tương đương nếu chúng có cùng tập nghiệm).
Chọn D:
Câu 5: Giải phương trình: cos3 x + sin3 x = cos2x
A. 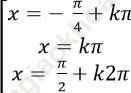
B. 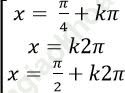
C. 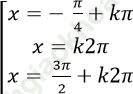
D. Đáp án khác
Ta có: cos3 x+ sin3 x= cos2x
⇒ (cosx+ sinx). (cos2x - cosx. sinx +sin2x) – cos2x= 0
⇒ (cosx+ sinx). (1 – cosx. sinx) – (cosx- sinx). (cosx+ sinx) = 0
⇒ (cosx+ sinx). (1 – cosx. sinx- cosx + sinx) = 0
⇒ (cosx+ sinx). [( 1+ sinx) – (cosx. sinx+ cosx)]=0
⇒ (cosx+ sinx)[ (1+ sinx) – cosx (sinx+ 1)]=0
⇒ (cosx+ sinx). (1- cosx). (1+ sinx) = 0
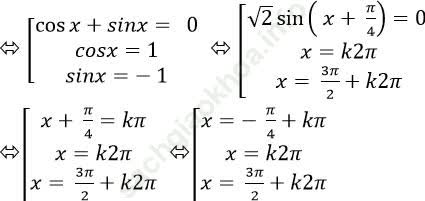
Chọn C.
Câu 6: Giải phương trình: sin (x + π/4) + sin2x + 1 = 0
A. 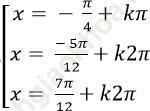
B. 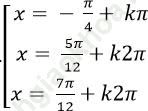
C. 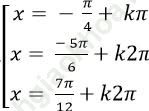
D. 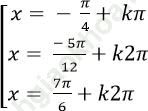

⇒ phương trình đã cho có ba họ nghiệm là (1); (2) và (3).
Chọn A.
Câu 7: Giải phương trình: ![]()
A. 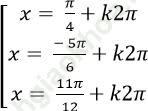
B. 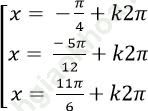
C. 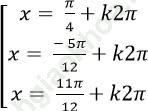
D. 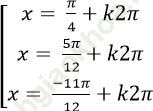
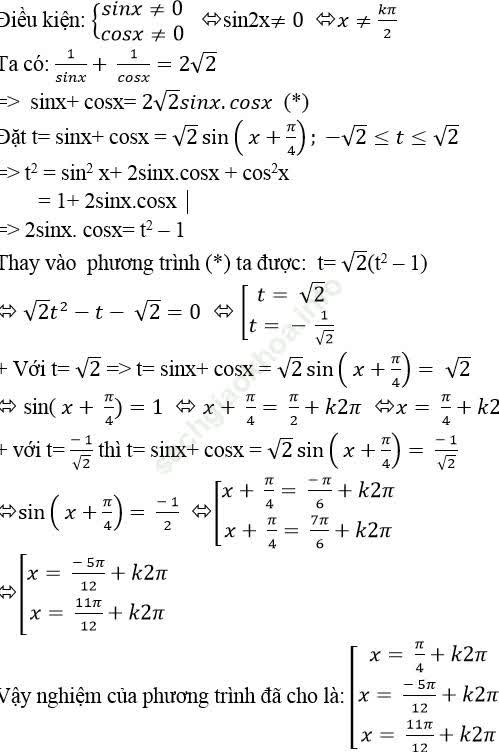
Chọn C.
Câu 8: Tìm nghiệm dương bé nhất của phương trình:
![]()
A. ![]()
B. ![]()
C. ![]()
D. ![]()

Chọn A.