Dạng 2: Phương trình bậc hai với một hàm số lượng giác - Chuyên đề Toán 11
A. Phương pháp giải & Ví dụ
Định nghĩa:
Phương trình bậc hai đối với một hàm số lượng giác là phương trình có dạng:
a. f2(x) + b. f (x) + c = 0
với f (x) = sinu (x) hoặc f (x) = cosu (x), tanu (x), cotu (x).
Cách giải:
Đặt t = f (x) ta có phương trình: at2 + bt +c = 0
Giải phương trình này ta tìm được t, từ đó tìm được x
Khi đặt t = sinu (x) hoặc t = cosu (x), ta có điều kiện: -1 ≤ t ≤ 1
Ví dụ minh họa
Bài 1:
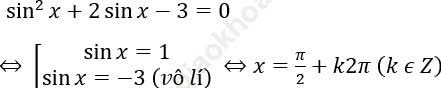
Bài 2:
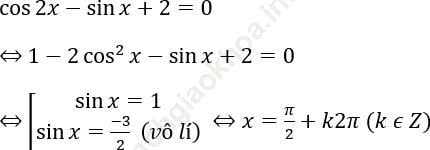
B. Bài tập vận dụng
Bài 1: 1/ (sin2 x) + tanx - 1 = 0
Bài giải:
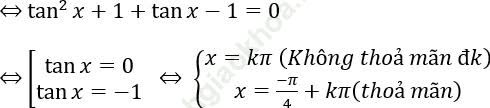
Bài 2: cosx – sin2x = 0
Bài giải:
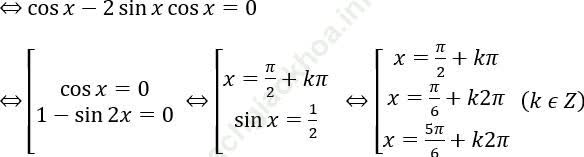
Bài 3: cos2x + cosx – 2 = 0
Bài giải:
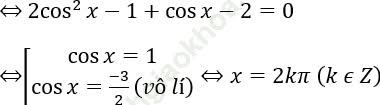
Bài 4: 1 + sin2x + cosx + sinx = 0
Bài giải:
1 + sin2x + cosx + sinx = 0
⇔ 1 + 2 sinx cosx + 2 (cosx+sinx) = 0
⇔ cos2x + sin2x + 2 sinxcosx + 2 (cosx + sinx) = 0
⇔ (sinx + cosx)2 + 2 (cosx + sinx) = 0
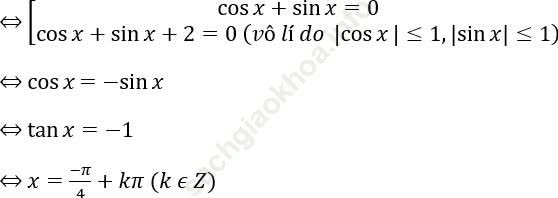
Bài 5: cos23xcos2x – cos2x = 0
Bài giải:
