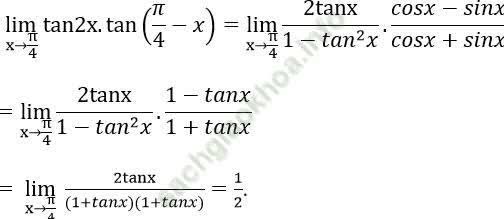Dạng 3: Tìm giới hạn hàm số dạng 0 nhân vô cùng - Chuyên đề Toán 11
A. Phương pháp giải & Ví dụ
Bài toán: Tính giới hạn
Ta có thể biến đổi: 
về dạng 0/0 hoặc ∞ /∞ rồi dùng các phương pháp tính giới hạn của hai dạng kia để làm.
Tuy nhiên, trong nhiều bài tập ta chỉ cần biến đổi đơn giản như đưa biểu thức vào trong (hoặc ra ngoài) dấu căn, quy đồng mẫu thức …. Là có thể đưa về dạng quen thuộc.
Ví dụ minh họa
Bài 1: Tính giới hạn: 
Bài giải:
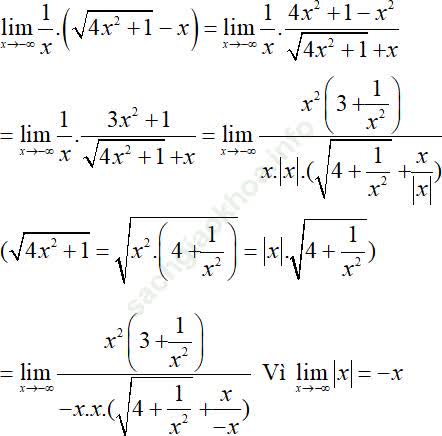
Bài 2: Tính giới hạn: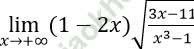 
Bài giải:
Bài 3: Tính giới hạn: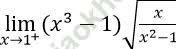
Bài giải:
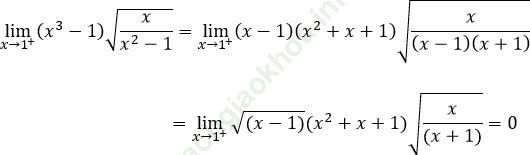
Bài 4: Tính giới hạn: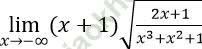 
Bài giải:
Bài 5: Tính giới hạn: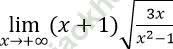
Bài giải:
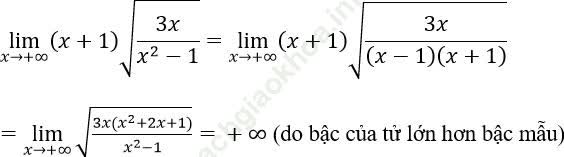
Bài 6: Tính giới hạn: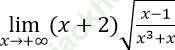 
Bài giải:
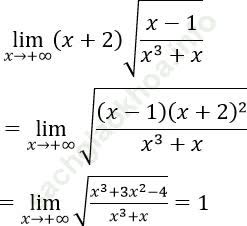
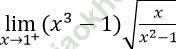
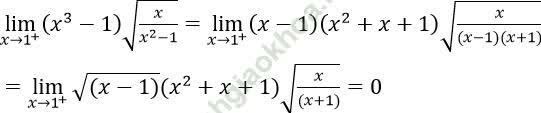
B. Bài tập vận dụng
Bài 1: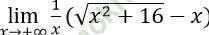 
bằng:
A. √5 B. 0 C. 5/2 D. +∞
Đáp án: B
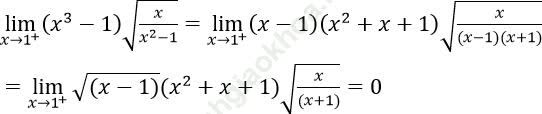
Đáp án B.
Bài 2: Chọn kết quả đúng trong các kết quả sau củ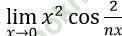a
là:
A. Không tồn tại B. 0 C. 1 D. +∞
Đáp án: A
Bài 3: Cho hàm số: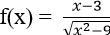
. Giá trị đúng của 
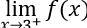là:
A. –∞
B. 0
C. √ 6
D. +∞
Đáp án: B
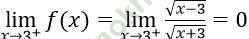
Đáp án B
Bài 4: Giới hạn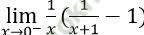 
bằng:
A. 0 B. -1 C. 1 D. -∞
Đáp án: B
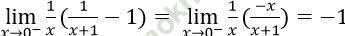
Đáp án B.
Bài 5: Giới hạn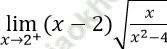 
bằng:
A. +∞ B. -∞ C. 0 D. 1
Đáp án: C
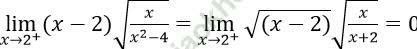
Đáp án C
Bài 6: Giới hạn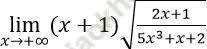
bằng:
A. -√ 2/2 B. √ 10/5 C. -√ 5/5 D. √ 2
Đáp án: B
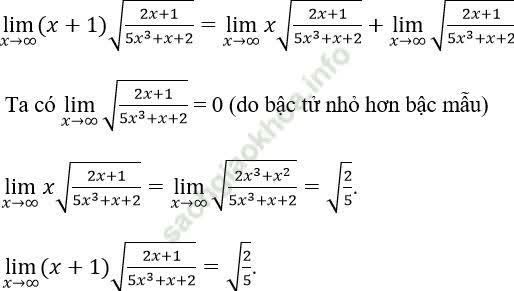
Đáp án B
Bài 7: Giới hạn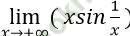 
bằng:
A. 0 B. 1 C. +∞ D. không tồn tại
Đáp án: B
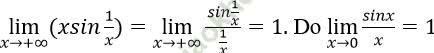
Đáp án B
Bài 8: Giới hạn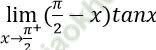
bằng:
A. 1 B. 0 C. -∞ D. không tồn tại
Đáp án: A
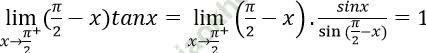
Đáp án A
Bài 9: Cho a là một số thực dương. Tính giới hạn: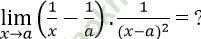
A. (-1/a2) B. +∞ C. -∞ D. không tồn tại
Đáp án: C
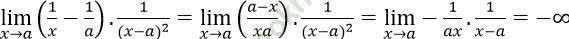
Đáp án C
Bài 10: Tính giới hạn: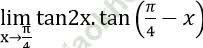 
A. 2 B. 0 C. 0.5 D. 0.25
Đáp án: C
