Cách tính tổng n số hạng đầu tiên của cấp số nhân cực hay có lời giải - Chuyên đề Toán 11
A. Phương pháp giải
Cho cấp số nhân (un) với công bội q ≠ 1. Khi đó tổng n số hạng đầu tiên được tính theo công thức: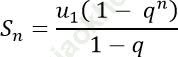 
B. Ví dụ minh họa
Ví dụ 1: Cho dãy số (un) xác định bởi: 
. Tính tổng: S = u2 + u4 + u6 +.. + u14
Bài giải:
* Ta có: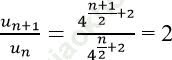 
với mọi n.
=> Dãy số (un) là cấp số nhân với u1 = 32 và công bội q = 2.
* Các số u2; u4; u6;... ; u14 lập thành cấp số nhân. Số hạng đầu u2 = u1. q = 64 và công bội q' = 2q = 4. Tổng của 7 số hạng u2; u4;... u14 là:
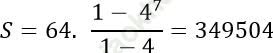
Đáp án đúng là: A.
Ví dụ 2: Cho cấp số nhân có 7 số hạng, số hạng thứ tư bằng 6 và số hạng thứ 7 gấp 243 lần số hạng thứ hai. Hãy tìm số hạng còn lại của cấp số nhân đó.
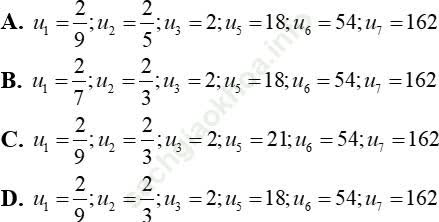
Bài giải:
Gọi cấp số nhân đó là (un) với 
.
Ta có: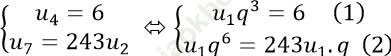 
Từ (2) ta có:
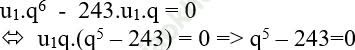
⇔ q = 3. Thay vào (1) ta được: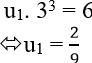 
Như vậy, các số hạng còn lại của cấp số nhân là:
Đáp án đúng là: D.
Ví dụ 3: Cho cấp số nhân (un) thỏa mãn.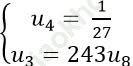 
. Tính tổng 20 số hạng đầu của cấp số nhân?
Bài giải:
Gọi q là công bội của cấp số nhân. Theo giả thiết ta có:
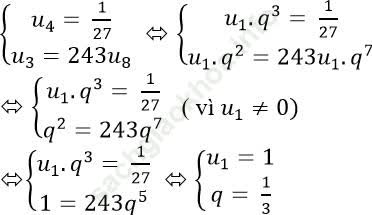
Tổng 20 số hạng đầu của cấp số nhân là:
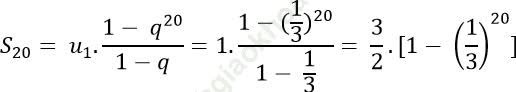
Đáp án đúng là: C.
Ví dụ 4: Cho cấp số nhân (un) thỏa mãn: 
. Tính u1?
Bài giải:
Theo bài ra ta có:
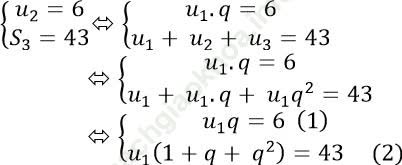
Lấy (1) chia (2), với u1 ≠ 0 ta được:
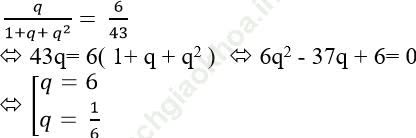
* Với q = 6 => u1 = 1.
* Với 
Vậy số hạng đầu tiên của cấp số nhân là 1 hoặc 36.
Đáp án đúng là: B.
Ví dụ 5: Cho cấp số cộng (un) thỏa mãn; 
. Hỏi tổng bao nhiêu số hạng đầu tiên bằng 3069?
Bài giải:
* Trước tiên ta đi tìm số hạng đầu tiên và công bội q của cấp số nhân.
Theo bài ra ta có:
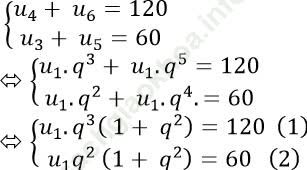
hay q = 2 thay vào (1) ta được u1 = 3.* Ta có tổng của n số hạng đầu tiên của cấp số nhân là:
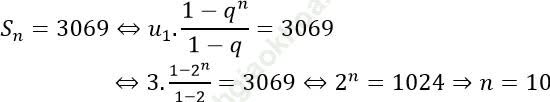
Kết luận tổng của 10 số hạng đầu tiên bằng 3069.
Đáp án đúng là: D.
Ví dụ 6: Tính tổng Sn = 3 + 32 + 33 +.... + 3n
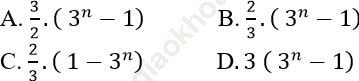
Bài giải:
Ta có dãy số 3; 32, 3333; .. ;3n là một cấp số nhân có n số hạng. Số hạng đầu là u1 = 3 và công bội q= 3.
=> Tổng của n số hạng đầu tiên là:
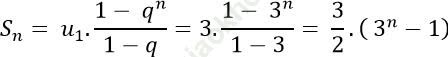
Đáp án đúng là: A.
Ví dụ 7: Tính: 
Bài giải:
Ta có:
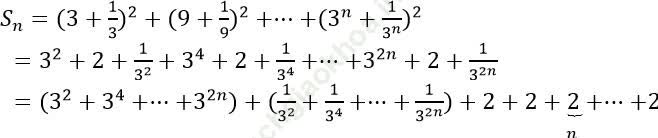
Dãy số 32; 34;.. ; 32n là cấp số nhân với n số hạng.
Số hạng đầu u1 = 32 và công bội q = 9.
Do đó: 
Có dãy số: 
là cấp số nhân với n số hạng, có số hạng đầu 
và công bội 
.
Do đó: 
Vậy: 
Đáp án đúng là: C.
Ví dụ 8: Tính: 
Bài giải:
Ta có:
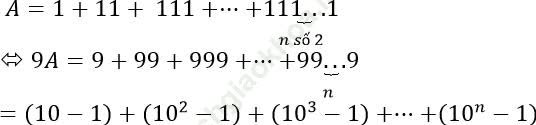
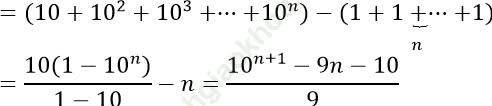
Vậy 
Đáp án đúng là: B.
Ví dụ 9: Cho cấp số nhân (un) có u1 = 2 và u2 = − 6. Biết rằng Sn = − 29524. Tính un.
Bài giải:
Ta có: u2 = u1. q nên − 6 = 2q ⇔ q = − 3
Lại có:
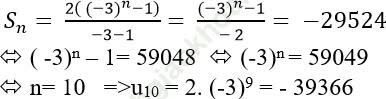
Đáp án đúng là: C.
C. Bài tập trắc nghiệm
Câu 1: Tính tổng: 
Đáp án: A
Ta có:
Nhận xét: dãy số 3,32, 33, 34,... , 320 là cấp số nhân với số hạng đầu là u1 = 3 và công bội q= 3.
=> Tổng 20 số hạng của dãy số là:
Câu 2: Tính tổng: 
Đáp án: B
Ta có dãy số (-1), (-1)2, (-1)3,…, (-1)41 là cấp số nhân gồm 41 số hạng với số hạng đầu là u1 = − 1 và công bội q = − 1.
Do đó tổng S bằng.
Câu 3: Cho cấp số nhân (un) có u1 = 3 và công bội là số nguyên tố bé nhất. Tìm k, biết Sk = 189.
Đáp án: D
Số nguyên tố bé nhất là 2 nên q = 2.
Ta có
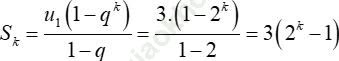
Theo giả thiết, ta có:
Câu 4: Tính tổng: 
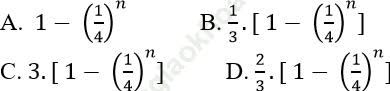
Đáp án: B
Ta có dãy số
Tổng n số hạng đầu tiên của dãy là:
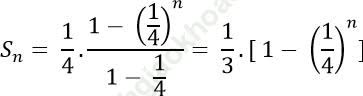
Câu 5: Tính tổng sau: 
Đáp án: B
* Nhận xét:
Nên:
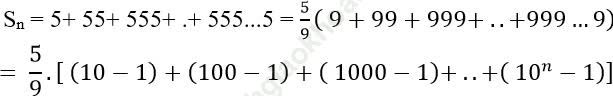
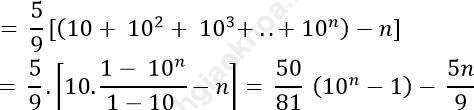
Vì 10+ 102 + 103 +.. + 10n là tổng của cấp số nhân; số hạng đầu u1 =10, công bội q = 10 nên
Câu 6: Tìm số hạng đầu tiên của cấp số nhân biết công bội q= 3, tổng số các số hạng là 728 và số hạng cuối bằng 486.
Đáp án: A
Theo đề bài ta có:
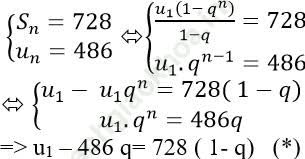
Thay q= 3 vào (*) ta được:
Câu 7: Tính tổng
Đáp án: A
Ta có:
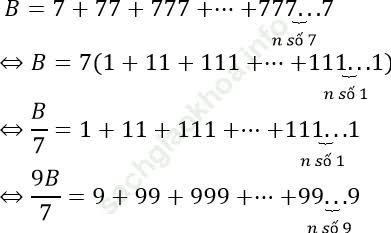
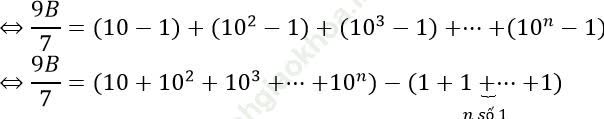
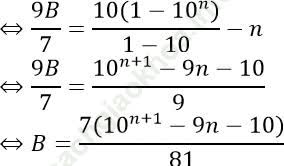
Câu 8: Cho dãy số (un) xác định bởi 
và 
.
Tổng: 
bằng.... ?
Đáp án: B
Đặt
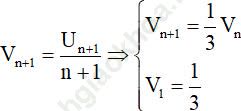
suy ra
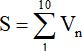
Do đó
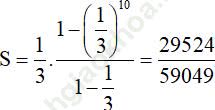
Câu 9: Cho cấp số nhân (un) thỏa mãn: u1 = 4; q = 2 và Sn = 2044. Tính S2n?
Đáp án: D
*Tổng của n số hạng đầu tiên của dãy là:
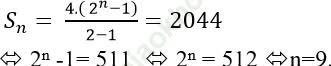
* Khi đó:
