Dạng 1: Tính đạo hàm bằng định nghĩa - Chuyên đề Toán 11
A. Phương pháp giải & Ví dụ
1. Định nghĩa đạo hàm tại một điểm
Cho hàm số y = f (x) xác định trên khoảng (a, b), xo ∈ (a, b). Nếu tồn tại, giới hạn (hữu hạn)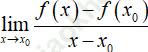 
thì giới hạn đó được gọi là đạo hàm của hàm số y = f (x) tại xo, kí hiệu là f' (xo) hay y’ (xo), tức là:
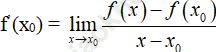
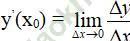
2. Quy tắc tính đạo hàm bằng định nghĩa
Bước 1: Với Δ x là số gia của đối số tại xo, tính: Δ y = f (xo + Δ x) - f (xo)
Lưu ý: Trong định nghĩa trên đây, thay xo bởi x ta sẽ có định nghĩa và quy tắc tính đạo hàm của hàm số y = f (x) tại điểm x ∈ (a, b)
Ví dụ minh họa
Bài 1: Cho hàm số 
có Δ x là số gia của đối số tại x = 2. Khi đó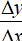 
bằng bao nhiêu?
Bài giải:
Tập xác định của hàm số đã cho là D = [2/3; +∞)
Với Δ x là số gia của đối số tại x = 2 sao cho 2 + Δ x ∈ D, thì:
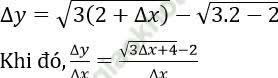
Bài 2: Cho hàm số f (x) = 3x + 5. Tính đạo hàm của hàm số đã cho bằng định nghĩa.
Bài giải:
Tập xác định của hàm số đã cho là D = R
Ta có Δ y = 3 (x+Δ x) + 5 - 3x - 5 = 3Δ x
Khi đó:
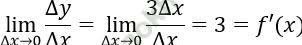
Bài 3: Cho hàm số: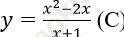 
Đạo hàm của hàm số đã cho tại x = 1?
Bài giải:
Với Δ x là số gia của đối số tại x = 1, ta có:
Bài 4: Tính đạo hàm của các hàm số sau tại các điểm đã cho: f (x)= 2x3 + 1 tại x = 2
Bài giải:
Ta có: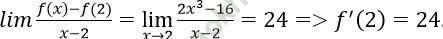 
Bài 5: Tính đạo hàm của các hàm số sau tại các điểm đã cho:
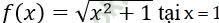
Bài giải:
Ta có: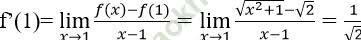 
Bài 6: Tính đạo hàm của hàm số:
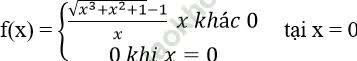
Bài giải:
Ta có: f (0) = 0, do đó:
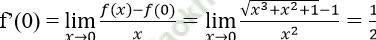
Bài 7: Tính đạo hàm của hàm số: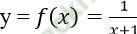
bằng định nghĩa
Bài giải:
Tập xác định của hàm số đã cho là D = R\ {-1}
Ta có:
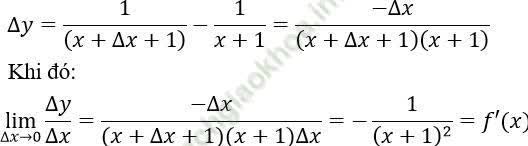
Bài 1: Cho hàm số f (x) = x2 + 2x, có Δ x là số gia của đối số tại x = 1, Δ y là số gia tương ứng của hàm số. Khi đó Δ y bằng:
A. (Δ x)2 + 2Δ x
B. (Δ x)2 + 4Δ x
C. (Δ x)2 + 2Δ x - 3
D. 3
Đáp án: B
Δ y = f (1 + Δ x) - f (1) = (1 + Δ x)2 + 2 (1 + Δ x) - (1 + 2) = (Δ x)2 + 4Δ x
Đáp án B
Bài 2: Cho hàm số: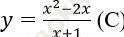 
Đạo hàm của hàm số đã cho tại x = 1 là:
A. 1/4 B. -1/2 C. 0 D. 1/2
Đáp án: A
Với Δ x là số gia của đối số tại x = 1, ta có
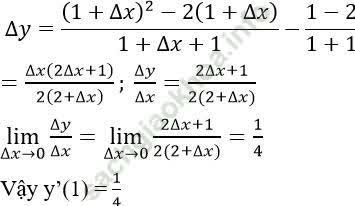
Đáp án A
Bài 3: Cho hàm số f (x) = |x + 1|. Khẳng định nào sau đây là sai?
A. f (x) liên tục tại x = -1
B. f (x) có đạo hàm tại x = -1
C. f (-1) = 0
D. f (x) đạt giá trị nhỏ nhất tại x = -1
Đáp án: B
Suy ra không tồn tại giới hạn của tỉ số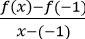
khi x → -1
Do đó hàm số đã cho không có đạo hàm tại x = -1
Vậy chọn đáp án là B
Bài 4: Số gia của hàm số f (x) = 2x2 - 1 tại x0 = 1 ứng với số gia Δ x = 0,1 bằng:
A. 1
B. 1,42
C. 2,02
D. 0,42
Đáp án: B
chọn đáp án là B
Bài 5: Cho hàm số y = √ x, Δ x là số gia của đối số tại x. Khi đó Δ y/Δ x bằng:
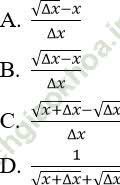
Đáp án: C
Δ y = f (x0 + Δ x) - f (x0)
Vậy chọn đáp án là C
Bài 6: Cho hàm số: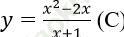
Đạo hàm của hàm số đã cho tại x = 1?
A. 1 B. 0 C. 1/4 D. -1/4
Đáp án: C
Ta có
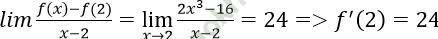
Vậy chọn đáp án là C
Bài 7: Đạo hàm của các hàm số sau tại các điểm đã cho: f (x) = 2x3 + 1 tại x = 2?
A. 10
B. 24
C. 22
D. 42
Đáp án: B
Ta có
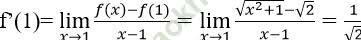
Vậy chọn đáp án là B
Bài 8: Đạo hàm của các hàm số sau tại các điểm đã cho:
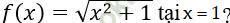
A. 1/2 B. -1/√ 2 C. 0 D. 3
Đáp án: A
Ta có f (0) = 0, do đó:
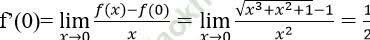
Vậy chọn đáp án là A
Bài 9: Hàm số: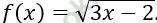 
có Δ x là số gia của đối số tại x = 2. Khi đó Δ y/Δ x bằng?
Đáp án: A
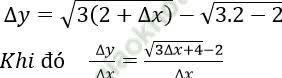
Vậy chọn đáp án là A
Bài 10: Đạo hàm của các hàm số sau tại các điểm đã cho: f (x) = x2 + 1 tại x = 1?
A. 1/2 B. 1 C. 0 D. 2
Đáp án: D
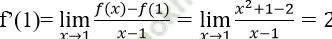
Vậy chọn đáp án là D