Khoảng cách từ một điểm đến một mặt phẳng (sử dụng hình chiếu) - Chuyên đề Toán 11
A. Phương pháp giải
Để tính được khoảng từ điểm A đến mặt phẳng (α) thì điều quan trọng nhất là ta phải xác định được hình chiếu của điểm A trên (α)
Cho trước SA ⊥ Δ; trong đó S ∈ (α) và Δ ⊂ (α)
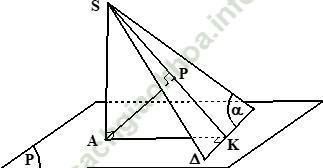
Bước 1: Dựng AK ⊥ Δ ⇒ Δ ⊥ (SAK) ⇒ (α) ⊥ (SAK) và (α) ∩ (SAK) = SK
Bước 2: Dựng AP ⊥ SK ⇒ AP ⊥ (α) ⇒ d (A, (α)) = AP
B. Ví dụ minh họa
Ví dụ 1: Trong mặt phẳng (P) cho tam giác đều ABC cạnh a. Trên tia Ax vuông góc với mặt phẳng (P) lấy điểm S sao cho SA = a. Khoảng cách từ A đến (SBC) bằng
Bài giải:
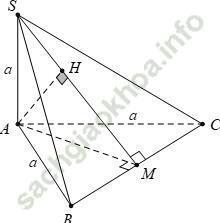
- Gọi M là trung điểm của BC, H là hình chiếu vuông góc của A trên SM
- Ta có BC ⊥ AM (trong tam giác đều đường trung tuyến đồng thời là đường cao). Và BC ⊥ SA (vì SA vuông góc với (ABC)). Nên BC ⊥ (SAM) ⇒ BC ⊥ AH
Mà AH ⊥ SM, do đó AH ⊥ (SBC)
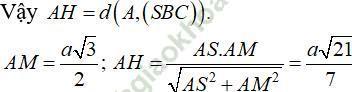
Đáp án đúng là: C
Ví dụ 2: Cho hình chóp S. ABCD có SA ⊥ (ABCD), đáy ABCD là hình chữ nhật. Biết AD = 2a; SA = a. Khoảng cách từ A đến (SCD) bằng:
Bài giải:
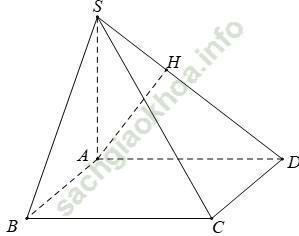
SA ⊥ (ABCD) nên SA ⊥ CD, AD ⊥ CD
Suy ra (SAD) ⊥ CD
Trong (SAD) kẻ AH vuông góc SD tại H
Khi đó AH ⊥ (SCD)
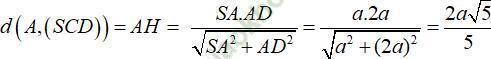
Đáp án đúng là: C
Ví dụ 3: Hình chóp đều S. ABC có cạnh đáy bằng 3a cạnh bên bằng 2a. Khoảng cách từ S đến (ABC) bằng:
A. 2a
B. a√ 3
C. a
D. a√ 5
Bài giải:
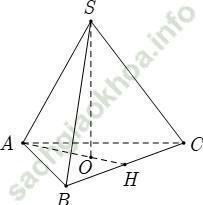
+ Gọi O là trọng tâm tam giác ABC. Do tam giác ABC đều nên O là tâm đường tròn ngoại tiếp tam giác ABC
+ Ta có: SA = SB = SC và OA = OB = OC nên SO là trục đường tròn ngoại tiếp tam giác ABC. Do đó SO ⊥ (ABC)
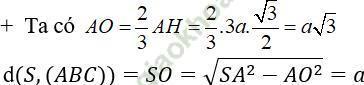
Đáp án đúng là: C
Ví dụ 4: Cho hình chóp S. ABC trong đó SA; AB; BC vuông góc với nhau từng đôi một. Biết SA = a√ 3, AB = a√ 3. Khoảng cách từ A đến (SBC) bằng:
Bài giải:
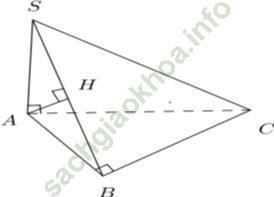
Đáp án đúng là: D
Kẻ AH ⊥ SB
Ta có: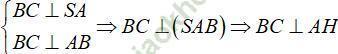 
Lại có: AH ⊥ SB nên AH ⊥ (SBC)
⇒ d (A; (SBC)) = AH
Trong tam giác vuông SAB ta có:
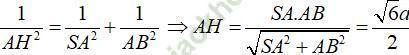
Ví dụ 5: Cho hình chóp S. ABCD có SA ⊥ (ABCD), đáy ABCD là hình chữ nhật. Biết AD = 2a; SA = a. Khoảng cách từ A đến (SCD) bằng:
Bài giải:
Đáp án đúng là: C
Kẻ AH ⊥ SD
Ta có: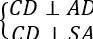 
nên CD ⊥ (SAD) ⇒ CD ⊥ AH (1)
Lại có; AH vuông góc SD (2)
Từ (1); (2) ⇒ AH ⊥ (SCD) và d (A, (SCD)) = AH
Trong tam giác vuông SAD ta có:
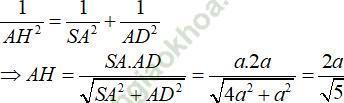
Ví dụ 6: Cho hình chóp tam giác đều S. ABC cạnh đáy bằng 2a và khoảng cách từ S đến mặt phẳng đáy bằng a√ 3. Tính khoảng cách từ tâm O của đáy ABC đến một mặt bên:
Bài giải:
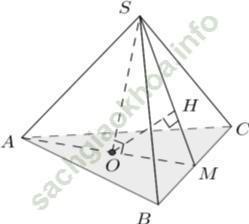
Đáp án đúng là: C
+ Gọi O là trọng tâm của tam giác ABC
Suy ra: OA = OB = OC (do tam giác ABC là tam giác đều)
Lại có: SA = SB = SC (vì S. ABC là hình chóp đều)
⇒ SO là trục của đường tròn ngoại tiếp tam giác ABC nên SO ⊥ (ABC) và SO = a√ 3
+ Gọi M là trung điểm của BC
Kẻ OH ⊥ SM, ta có
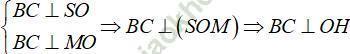nên suy ra d (O; (SBC)) = OH.
Ta có: OM = (1/3).AM = (a√ 3)/3
Xét tam giác vuông SOM đường cao OH có:
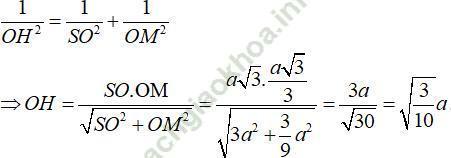
C. Bài tập vận dụng
Câu 1: Cho tứ diện đều ABCD có cạnh bằng a. Khoảng cách từ A đến (BCD) bằng:
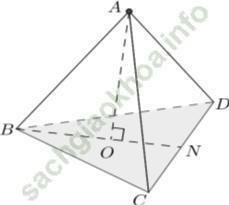
Chọn B
Gọi O là trọng tâm tam giác BCD
⇒ OB = OC = OD (do tam giác BCD là tam giác đều)
Lại có: AB = AC = AD = a
⇒ AO là trục đường tròn ngoại tiếp tam giác BCD
⇒ AO ⊥ (BCD)
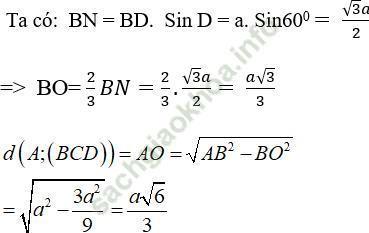
Câu 2: Cho hình chóp S. ABCD có đáy là hình thoi tâm O cạnh a và có góc ∠ BAD = 60°. Đường thẳng SO vuông góc với mặt phẳng đáy (ABCD) và SO = 3a/4. Khoảng cách từ O đến mặt phẳng (SBC) là:
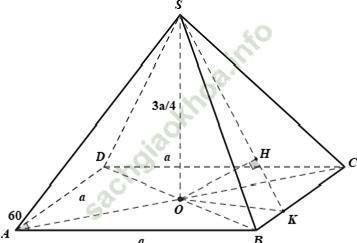
Chọn C
+ Trong mặt phẳng (ABCD), kẻ OK ⊥ BC (K ∈ BC)
+ Mà BC ⊥ SO nên suy ra hai mặt phẳng (SOK) và (SBC) vuông góc nhau theo giao tuyến SK.
+ Trong mặt phẳng (SOK), kẻ OH ⊥ SK (H ∈ SK)
Suy ra: OH ⊥ (SBC) ⇒ d (O, (SBC)) = OH
+ Xét mp (ABCD) có:
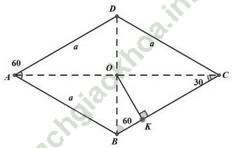
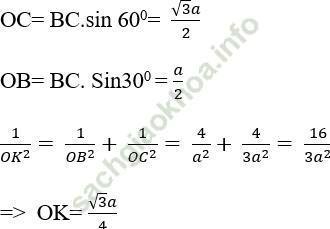
+ xét tam giác SOK vuông tại O ta có:
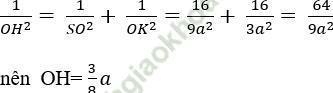
Câu 3: Cho hai tam giác ABC và ABD nằm trong hai mặt phẳng hợp với nhau một góc 60°; tam giác ABC cân tại C, tam giác ABD cân ở D. Đường cao DM của tam giác ABD bằng 12 cm. Khoảng cách từ D đến (ABC) bằng
A. 3√ 3 cm B. 6√ 3 cm C. 6 cm D. 6√ 2 cm
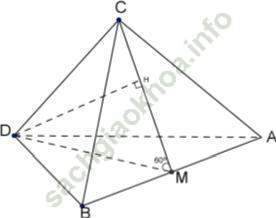
+ Gọi M là trung điểm AB.
Do tam giác ABC cân tại C và tam giác ABD cân tại D nên CM ⊥ AB; DM ⊥ AB suy ra: AB ⊥ (CDM)
+ Do hai tam giác ABC và ABD nằm trong hai mặt phẳng hợp với nhau một góc 60° nên ∠ CMD = 60°
+ Gọi H là hình chiếu vuông góc của D lên CM
⇒ DH = d (D, (ABC))
Xét tam giác DHM có:
DH = DM. Sin 60° = 6√ 3
Chọn đáp án B
Câu 4: Cho hình lập phương ABCD. A’B’C’D’ cạnh a. Khoảng cách từ A đến (B’CD’) bằng
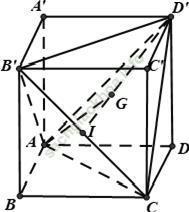
Ta có: AB’ = AC = AD’ = B’D’ = B’C = CD’ = a√ 2
⇒ Tứ diện AB’CD’ là tứ diện đều.
Gọi I là trung điểm B’C và G là trọng tâm tam giác B’CD’.
Ta có: AC = AD’ = AB’ và GB’ = GC = GD’
nên AG ⊥ (B'CD')
Khi đó ta có: d (A, (B’CD’)) = AG
Vì tam giác B’CD’ đều cạnh a√ 2 nên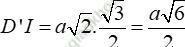 
Theo tính chất trọng tâm ta có: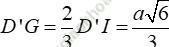 
Trong tam giác vuông AGD’ có:
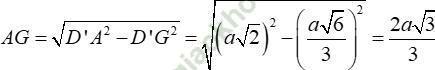
Chọn C
Câu 5: Cho hình chóp S. ABC có đáy ABC là tam giác vuông cân tại A với AB = a. Mặt bên chứa BC của hình chóp vuông góc với mặt đáy, hai mặt bên còn lại đều tạo với mặt đáy một góc 45°. Tính khoảng cách từ điểm S đến mặt phẳng đáy (ABC).
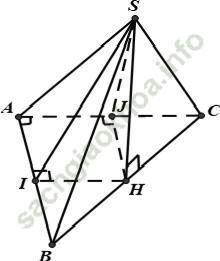
Gọi H là hình chiếu của S lên (ABC), vì mặt bên (SBC) vuông góc với (ABC) nên H ∈ BC
Dựng HI ⊥ AB, HJ ⊥ AC, theo đề bài ta có ∠ SIH = ∠ SJH = 45°.
Do đó: Δ SHI = Δ SHJ (cạnh góc vuông - góc nhọn)
Suy ra: HI = HJ
Lại có ∠ B = ∠ C = 45° ⇒ Δ BIH = Δ CJH ⇒ HB = HC
Vậy H trùng với trung điểm của BC
Từ đó ta có HI là đường trung bình của tam giác ABC nên HI = AC/2 = a/2
Tam giác SHI vuông tại H và có ∠ SIH = 45° ⇒ Δ SHI vuông cân.
Do đó: SH = HI = a/2
Chọn đáp án A
Câu 6: Cho hình chóp tam giác đều S. ABC có cạnh bên bằng b cạnh đáy bằng d, với d < b√ 3. Hãy chọn khẳng định đúng trong các khẳng định bên dưới.
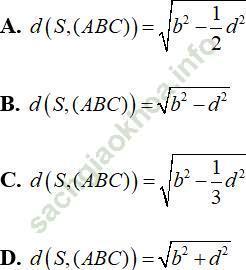
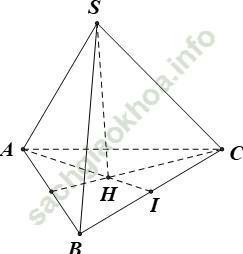
Gọi I là trung điểm của BC và H là trọng tâm tam giác ABC.
Do S. ABC là hình chóp đều nên SH ⊥ (ABC) ⇒ d (S, (ABC)) = SH
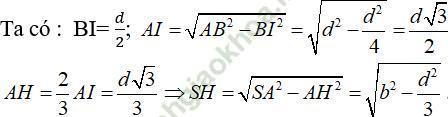
Chọn C
Câu 7: Cho hình lập phương ABCD. A1B1C1D1 cạnh bằng a. Gọi M là trung điểm của AD. Khoảng cách từ A1 đến mặt phẳng (C1D1M) bằng bao nhiêu?
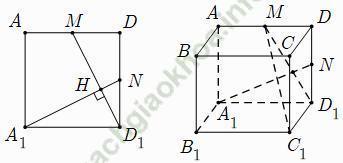
Gọi N là trung điểm cạnh DD1 và
Ta có: Δ A1ND1 = Δ D1MD (c. g. c)
Chọn đáp án A
Câu 8: Cho hình chóp tam giác đều S. ABC có cạnh đáy bằng 3a cạnh bên bằng 2a. Khoảng cách từ S đến mặt phẳng (ABC) bằng:
A. 4a B. 3a C. a D. 2a
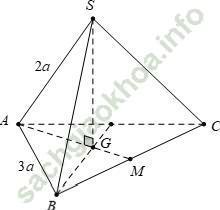
Gọi G là trọng tâm tam giác ABC
Do S. ABC là hình chóp đều nên SG ⊥ (ABC)
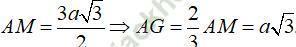
Tam giác SAG vuông tại G có:
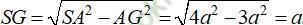
Chọn đáp án C
Câu 9: Cho hình chóp tứ giác đều S. ABCD có cạnh đáy bằng a và chiều cao bằng a√ 2. Tính khoảng cách từ tâm O của đáy ABCD đến một mặt bên:
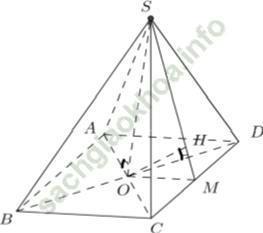
Chọn B
Gọi O là tâm của hình vuông ABCD và M là trung điểm của CD
Do hình chóp S. ABCD là hình chóp tứ giác đều nên SO ⊥ (ABCD)
Kẻ OH ⊥ SM, ta có:
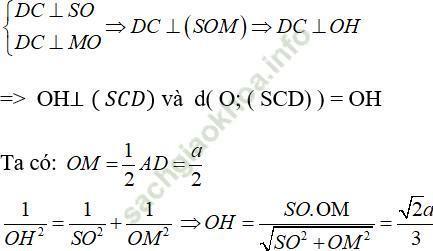
Câu 10: Cho hình chóp S. ABCD có mặt đáy là hình thoi tâm O, cạnh a và góc ∠ BAD = 120°, đường cao SO = a. Tính khoảng cách từ điểm O đến mặt phẳng (SBC).
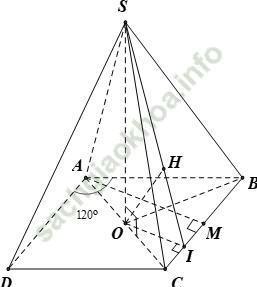
Vì hình thoi ABCD có ∠ BAD bằng 120° nên ∠ ABC = 60°
⇒ tam giác ABC đều cạnh a.
Kẻ đường cao AM của tam giác ABC ⇒ AM = a√ 3/2
Kẻ OI ⊥ BC tại I ⇒ OI = AM/2 = a√ 3/4.
Kẻ OH ⊥ SI ⇒ OH ⊥ (SBC)
⇒ d (O; (SBC)) = OH
Xét tam giác vuông SOI ta có:
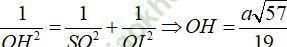
Chọn D
Câu 11: Cho hình chóp S. ABCD có mặt đáy ABCD là hình thoi cạnh a, ∠ ABC = 120°. Hình chiếu vuông góc của đỉnh S lên mặt phẳng (ABCD) là trọng tâm G của tam giác ABD, ∠ ASC = 90°. Khoảng cách từ điểm A đến mặt phẳng (SBD) tính theo a bằng
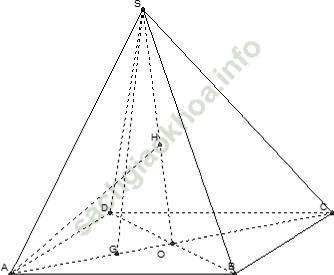
Xác định khoảng cách:
- Ta có đáy ABCD là hình thoi, góc ∠ ABC = 120° nên ∠ ABD = 60° và tam giác ABD đều cạnh a
Ta có: AC = a√ 3, AG = a√ 3/3
Tam giác SAC vuông ở S, có đường cao SG nên
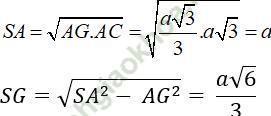
Xét hình chóp S. ABD có chân đường cao trùng với tâm của đáy nên SA = SB = SD = a.
- Dựng hình chiếu của A lên mặt phẳng (SBD): Kẻ đường cao AH của tam giác SAO với O là tâm của hình thoi.
AH = a√ 6/3
Cách khác: Nhận xét tứ diện S. ABD có tất cả các cạnh bằng a. Do đó S. ABD là tứ diện đều, vậy AH = SG = a√ 6/3
Chọn đáp án D
Câu 12: Cho hình chóp S. ABCD có đáy là hình chữ nhật, AB = a; AC = 2a và SA vuông góc với mặt phẳng (ABCD); SC tạo với mặt phẳng (SAB) một góc 30°. Gọi M là một điểm trên cạnh AB sao cho BM = 3MA. Khoảng cách từ điểm A đến mặt phẳng (SCM)?
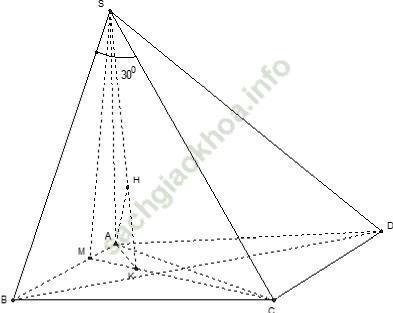
+ Ta có: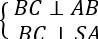 
nên BC ⊥ (SAB)
Khi đó; SC tạo với mặt phẳng (SAB) góc 30° nên ∠ CSB = 30°
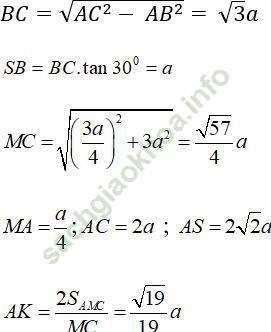
+ Xác định khoảng cách: d (A; (SBC)) = AH
Tính AH:
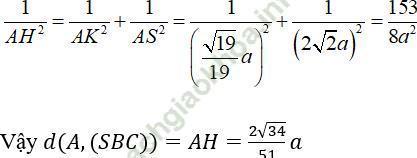
Chọn đáp án B
Câu 13: Cho hình chóp S. ABCD có đáy ABCD là hình chữ nhật, mặt bên SAD là tam giác vuông tại S hình chiếu vuông góc của S lên mặt phẳng (ABCD) là điểm H thuộc cạnh AD sao cho HA = 3 HD. Gọi M là trung điểm của cạnh AB. Biết rằng SA = 2√ 3. a và đường thẳng SC tạo với mặt đáy một góc 30°. Khoảng cách từ M đến mặt phẳng (SBC) tính theo a bằng
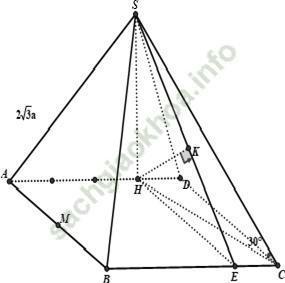
+ SC có hình chiếu vuông góc lên mp (ABCD) là HC ⇒ (SC, (ABCD)) = ∠ SCH = 30°
Đặt AD = 4x (x > 0)
Xét tam giác SAD vuông tại S ta có:
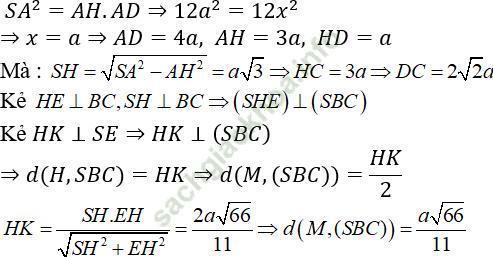
Chọn D
Câu 14: Cho hình chóp S. ABC có đáy ABC là tam giác đều cạnh a. Gọi I là trung điểm của cạnh AB. Hình chiếu vuông góc của đỉnh S lên mặt phẳng đáy là trung điểm H của CI góc giữa đường thẳng SA và mặt đáy bằng 60°. Khoảng cách từ điểm H đến mặt phẳng (SAC) là
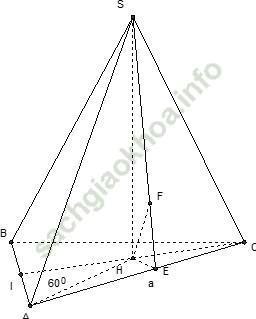
Chọn A
+ Do góc giữa SA và mp (ABC) là 60° nên ∠ SAH = 60°
+ Ta có; CI = CA. sin60° = (a√ 3)/2; AI = AB/2 = a/2
Trong tam giác ACI có trung tuyến AH suy ra
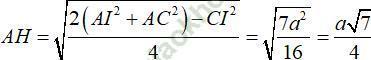
Trong tam giác SHA vuông tại H và ∠ SAH = 60° suy ra SH = AH √ 3 = a√ 21/4
Gọi E; F lần lượt là hình chiếu của H trên AC và SE. Khi đó d (H; (SAC)) = HF
