Phương trình lượng giác đưa về dạng tích - Chuyên đề Toán 11

A. Phương pháp giải

+ Để đưa một phương trình lượng giác về dạng tích ta cần sử dụng linh hoạt các công thức lượng giác: Công thức cộng; công thức nhân đôi; công thức hạ bậc; công thức biến đổi tổng thành tích; tích thành tổng...

+ Sau khi đưa được phương trình về dạng tích: A. B = 0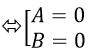

Giải từng phương trình A = 0; B= 0

B. Ví dụ minh họa

Ví dụ 1: Giải phương trình 1+ cosx + cos² x + cos3x – sin² x = 0

A.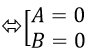

B.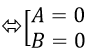

C.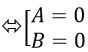

D.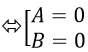

Bài giải:

Đáp án đúng là: B

Hướng dẫn:

Ta có: 1+ cosx + cos² x+ cos3x – sin² x=0

⇒ (1- sin² x)+ cos² x+ (cosx+ cos3x)=0

⇒ cos² x+ cos² x + 2. cos 2x. cos x= 0

⇒ 2cos² x + 2cos2x. cosx=0

⇒ 2cosx. (cosx + cos2x) = 0

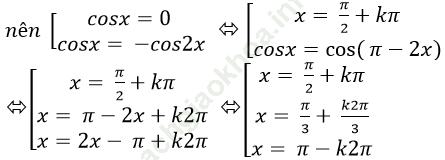
Ví dụ 2: Phương trình sin3x – 4sinx. cos2x = 0 có các nghiệm là:

A. x = k2π

B. x = π/2+kπ

C. x = kπ

D. x = π/2 + k2π

Bài giải:

Đáp án đúng là: C.

Hướng dẫn:

Ta có: sin 3x - 4sinx. cos2x = 0

⇒ sin3x - 2 [sin3x + sin (-x)] = 0

⇒ sin3x - 2sin3x + 2sinx = 0 (vì sin (-x) = - sinx)

⇒ 2sinx = -sin3x

⇒ 2sinx = 4sin³ x - 3sinx

⇒ 2sinx – 4sin³ x + 3sinx= 0

⇒ 5sinx – 4sin³ x = 0

⇒ sinx (5- 4sin² x) = 0

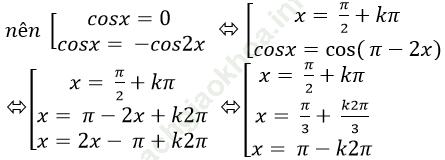
Vậy nghiệm của phương trình đã cho là: x = kπ

Ví dụ 3. Giải phương trình: ( -sinx + cosx) (1 + sinx) = cos² x

A.

B.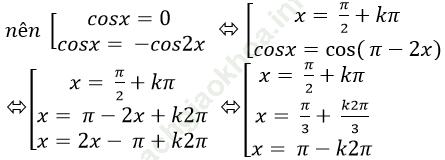

C.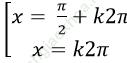

D.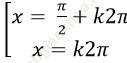

Bài giải:

Đáp án đúng là: D.

Hướng dẫn:

Ta có: (- sinx + cosx). (1 + sinx) = cos²x

⇒ (- sinx + cosx). (1 + sinx) - cos² x = 0

⇒ (-sinx + cosx). (1 + sinx) – (1 - sin² x) = 0

⇒ (- sinx + cosx). (1 + sinx) – (1- sinx). (1 + sinx) = 0

⇒ (1 + sinx). (- sinx + cosx – 1 + sinx) = 0

⇒ (1 + sinx). (cosx- 1) = 0

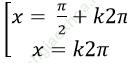
Ví dụ 4. Giải phương trình: 2 + sin2x – 2cos² x = 0

A.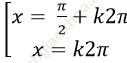

B.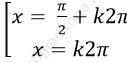

C.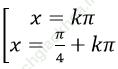

D.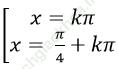

Bài giải:

Đáp án đúng là: A

Hướng dẫn:

Ta có: 2 + sin2x – 2cos² x = 0

⇒ sin 2x + (2 - 2cos² x) = 0

⇒ 2sinx. cosx + 2sin² x = 0

⇒ 2sinx (cosx + sinx) = 0

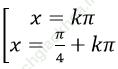
Ví dụ 5: Giải phương trình: cos² 4x + sin²2x = 1

A.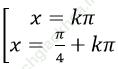

B.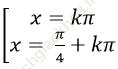

C. Cả A và B đúng

D. Đáp án khác

Bài giải:

Đáp án đúng là: C.

Hướng dẫn:

Ta có: cos² 4x + sin² 2x= 1

⇒ cos²4x + sin² 2x- 1=0

⇒ cos² 4x- cos² 2 x=0

⇒ (cos 4x- cos2x). (cos4x+ cos2x) = 0

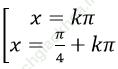
Ví dụ 6: Phương trình 4cosx – 2cos 2x – cos4x = 1 có các nghiệm là:

A.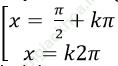

B.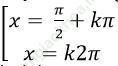

C.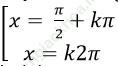

D.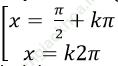

Bài giải:

Đáp án đúng là: A.

Hướng dẫn:

Ta có: 4cosx - 2cos2x – cos4x = 1

⇒ 4cosx – 2cos 2x – (2cos²2x – 1) – 1 = 0

⇒ 4cosx – 2cos2x - 2cos² 2x = 0

⇒ 4cos x - 2cos2x (1 + cos2x) = 0

⇒ 4cosx - 2cos2x. 2cos² x = 0

⇒ 4cosx. (1 – cos 2x. cosx) = 0

⇒ 4cosx. [ 1- (2cos² x - 1). cos x] = 0

⇒ 4cos x. [1- 2cos³ x + cosx] = 0

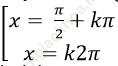
Ví dụ 7: Phương trình cosx - 1 + 2sinx – sin2x = 0 có nghiệm là:

A.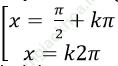

B.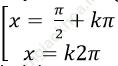

C.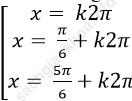

D.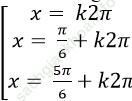

Bài giải:

Đáp án đúng là: C.

Hướng dẫn:

Ta có: cosx - 1 + 2sinx – sin2x = 0

⇒ (cosx - sin2x) + (2sinx - 1) = 0

⇒ (cosx – 2. sinx. cosx) + (2sinx - 1) = 0

⇒ cosx (1 - 2sinx) – (1 - 2sinx) = 0

⇒ (cosx - 1). (1 - 2sinx) = 0

Ví dụ 8: Giải phương trình: sin3x – 1 = 2sinx. cos2x – cos2x

A.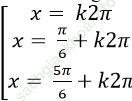

B.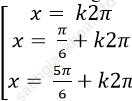

C.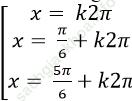

D. Đáp án khác

Bài giải:

Đáp án đúng là: B.

Hướng dẫn:

Ta có: sin3x- 1= 2sinx. cos2x- cos2x

⇒ sin 3x- 1= sin3x + sin (-x) – cos2 x

⇒ sin 3x- 1 = sin3x – sin x – cos 2x

⇒ (sin3x- sin3x) + (cos2x – 1) + sinx = 0

⇒ - 2sin²x + sin x = 0

⇒ sinx (- 2sinx + 1) = 0

Ví dụ 9. Giải phương trình: cot2x + 3tan 3x = 2tan2x

A. x = π/4 + kπ

B. x = kπ

C. x = π/2 + kπ

D. Vô nghiệm

Bài giải:

Đáp án đúng là: D.

Hướng dẫn:

Điều kiện: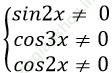

Ta có; cot2x + 3tan3 x = 2tan2x

⇒ (cot2x + tan 3x) + (2tan3x - 2tan2x) = 0

⇒ cosx. cos2x + 2sinx. sin2x = 0

⇒ (cosx. cos2x + sinx. sin2x) + sinx. sin2x = 0

⇒ cosx + sinx. 2sinx. cosx = 0

⇒ cosx. (1 + 2sin² x) = 0

⇒ cosx = 0 (vì 1 + 2sin2 x > 0 với mọi x)

⇒ x = π/2 + kπ

Kết hợp với điều kiện suy ra phương trình đã cho vô nghiệm

Ví dụ 10. Giải phương trình: 4cos⁵x. sinx – 4sin⁵ x. cosx = cos²2x

A.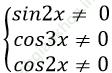

B.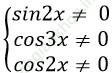

C.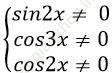

D. Đáp án khác

Bài giải:

Đáp án đúng là: B

Hướng dẫn:

Ta có: 4cos⁵x. sinx – 4sin⁵ x. cosx = cos²2x

⇒ 4cosx. sinx. ( cos⁴ x- sin⁴ x) = cos² 2x

⇒ 4. cosx. sinx. ( cos² x –sin² x). (cos² x+ sin² x) – cos² 2x = 0

⇒ 2sin2x. cos2x. 1 – cos² 2x= 0

⇒ cos2x (2sin2x – cos2x) = 0

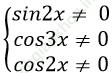
Ví dụ 11. Tìm nghiệm dương nhỏ nhất của phương trình: cos⁴x – cos2x + 2sin⁶ x = 0

A. x = π/2

B. x = π

C. x = π/3

D. x = π/4

Bài giải:

Đáp án đúng là: B

Hướng dẫn:

Ta có: cos⁴x – cos2x + 2sin⁶ x = 0

⇒ (1- sin² x)² – (1- 2sin² x) + 2sin⁶ x = 0

⇒ 1 – 2sin² x + sin⁴ x – 1 + 2sin²x + 2sin⁶ x = 0

⇒ sin⁴ x + 2sin⁶ x = 0

⇒ sin⁴ x. ( 1 + 2sin² x) = 0

⇒ sin⁴ x = 0 (vì 1 + 2sin² x > 0 với mọi x)

⇒ sinx = 0 ⇒ x = kπ

⇒ Nghiệm dương nhỏ nhất của phương trình là x = π (khi đó k = 1)

Ví dụ 12. Tìm nghiệm dương nhỏ nhất của phương trình: cos2x + cos22x+ cos23x = 1

A. x= π/3

B. x= π/4

C. x= π/6

D. x= π/2

Bài giải:

Đáp án đúng là: C.

Ta có: cos2x + cos22x + cos23x = 1

⇒ 1+cos2x+ 1+ cos4x+ 1+ cos 6x= 2

⇒ (cos 2x+ cos 6x)+ cos4x + 1 = 0

⇒ 2cos4x. cos2x + 2cos2 2x= 0

⇒ 2cos 2x. ( cos 4x+ cos2x)= 0

⇒ 2cos2x. 2. cos3x. cosx = 0

⇒ Nghiệm dương nhỏ nhất của phương trình là x = π/6

Ví dụ 13. Tìm nghiệm âm lớn nhất của phương trình:

A.

B.

C.

D.

Bài giải:

Đáp án đúng là: D.

Hướng dẫn:

Ví dụ 14. Giải phương trình: sin²2x + sin² 4x = cos² 2x + cos² 4x

A.

B.

C.

D.

Bài giải:

Đáp án đúng là: B.

Hướng dẫn:

Ta có: sin²2x + sin² 4x = cos² 2x + cos² 4x

⇒ (sin² 2x – cos²2x) + (sin²4x – cos²4x) = 0

⇒ - cos4x – cos8x = 0

⇒ cos4x + cos 8x = 0

⇒ 2. cos 6x. cos2x= 0

C. Bài tập vận dụng

Câu 1: Giải phương trình sin2x. ( cotx + tan2x) = 4cos² x

A.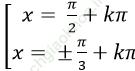

B.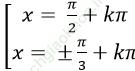

C.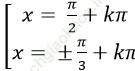

D.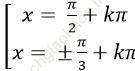

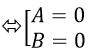
Hiển thị lời giải

Chọn D.

Câu 2: Giải phương trình: cos³ x - sin³ x = 1 - 2sin² x

A.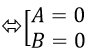

B.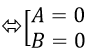

C.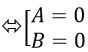

D.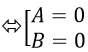

Hiển thị lời giải

Do 1- 2sin² x= sin² x+ cos² x- 2sin² x= cos² x- sin² x

Nên: cos² x – sin² x = 1- 2sin² x

⇒ (cosx – sinx). (cos² x + cosx. sinx + sin² x) = cos² x- sin² x

⇒ (cosx- sinx). (1+ cosx. sinx) – (cos² x –sin² x)= 0

⇒ (cosx- sinx). (1 + cosx. sinx) - (cosx- sinx). (cosx+ sinx) = 0

⇒ (cosx- sinx). (1 + cosx. sinx – cosx- sinx) = 0

⇒ (cosx- sinx). [(1- cosx) - (- cosx. sinx + sinx) = 0

⇒ (cosx- sinx). [( 1- cosx) - sinx (1- cosx)]= 0

⇒ (cosx- sinx). (1- cosx) (1- sinx) = 0

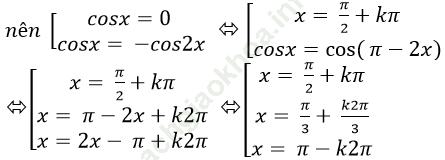
Chọn A.

Câu 3: Giải phương trình: 1+ sinx+ cosx + tanx = 0

A.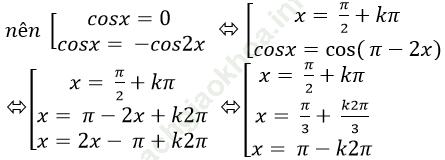

B.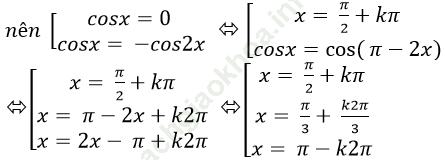

C.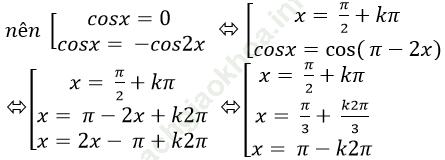

D.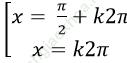

Hiển thị lời giải

Điều kiện: cosx ≠ 0

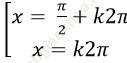
Chọn B

Câu 4: Một họ nghiệm của phương trình 2sin2x – 2sinx = cot x – 1.

A.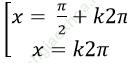

B.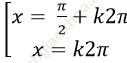

C.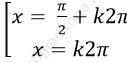

D. Tất cả sai

Hiển thị lời giải

Điều kiện: sinx ≠ 0

Ta có: 2sin2x – 2sinx = cot x- 1

⇒ 2sin2x -2sinx – cotx + 1 = 0

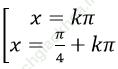
+ Nếu 2cosx. sinx + cosx- sinx = 0 hay sinx- cosx – 2sinx. cosx=0 (*)

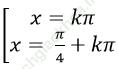
Chọn A.

Câu 5: Giải phương trình sin³ x+ cos³x= 2sin⁵ x+ 2cos⁵x.

A.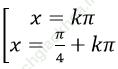

B.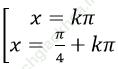

C.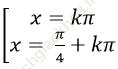

D.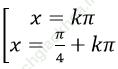

Hiển thị lời giải

Ta có: sin³ x+ cos³x= 2sin⁵ x+ 2cos⁵x.

⇒ (sin³ x – 2sin⁵x) + (cos³ x – 2cos⁵ x) = 0

⇒ sin³ x (1- 2sin² x) + cos³ x. ( 1- 2cos² x) = 0

⇒ sin³ x. cos2x + cos³ x. (-cos2x) = 0

⇒ cos 2x. ( sin³ x – cos³x) = 0

⇒ cos2x. (sinx- cosx). (sin² x+ sinx. cosx + cos²x) =0

⇒ cos 2x. (sinx- cosx). (1+ sinx. cosx) = 0

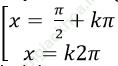
Chọn B.

Câu 6: Giải phương trình: tanx + tan 2x = - sin3x. cos2x

A. x = kπ/6

B. x = kπ/4

C. x = kπ/3

D. Cả A và B đúng

Hiển thị lời giải

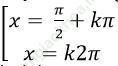
Chọn C.

Câu 7:Giải phương trình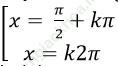

A.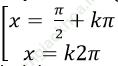

B.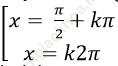

C.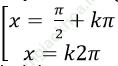

D.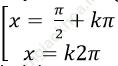

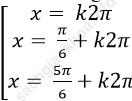
Hiển thị lời giải

Chọn D.

Câu 7: Phương trình 2√ 2. sin 5x. cos 3x = sin4x + 2√ 2 sin3x. cos 5x có nghiệm là:

A. x= kπ/2

B. x= kπ

C.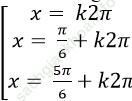

D.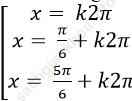

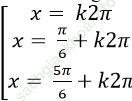
Hiển thị lời giải

Chọn A.

Câu 8: Giải phương trình cosx – sinx = sin2x - 2cos² x:

A.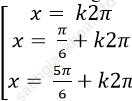

B.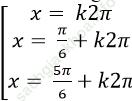

C.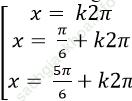

D.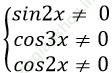

Hiển thị lời giải

Ta có: cosx- sinx= sin2x -2cos²x

⇒ cosx – sinx - (sin2x – 2cos² x) = 0

⇒ (cosx- sinx) - (2. sinx. cosx – 2cos² x) = 0

⇒ (cosx – sinx) – 2cosx (sinx – cosx) = 0

⇒ (cosx- sinx). (1- 2cosx) = 0

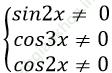
Chọn C.

Câu 9:Đâu không là một họ nghiệm của phương trình: sin2 x+ sin²2x + sin²3x=2 là.

A.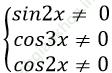

B.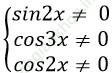

C.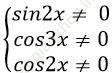

D.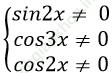

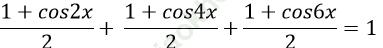
Hiển thị lời giải

Chọn A.

Câu 10: Tìm nghiệm âm lớn nhất của phương trình: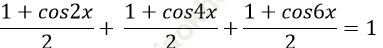

A.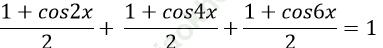

B.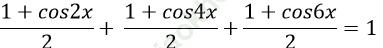

C.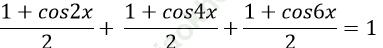

D.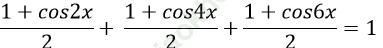

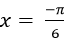
Hiển thị lời giải

Chọn B.

Câu 10:Phương trình 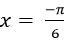có bao nhiêu họ nghiệm?

A. 2

B. 3

C. 4

D. 1

Hiển thị lời giải

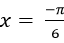
Kết hợp điều kiện suy ra phương trình đã cho có ba họ nghiệm

Chọn B

Câu 11:Phương trình: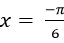 có nghiệm là:

A.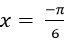

B.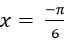

C.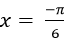

D. Đáp án khác

Hiển thị lời giải

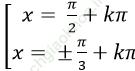
Chọn D

Câu 12: Giải phương trình: sin²3x + cos²6x = sin² 5x +cos² 4x

A.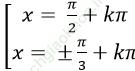

B.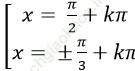

C.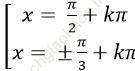

D.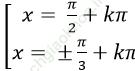

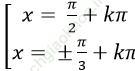
Hiển thị lời giải

⇒ 1- cos 6x+ 1+ cos12x= 1- cos10x + 1+ cos 8x

⇒ - cos 6x+ cos12x = - cos10x + cos 8x

⇒ (cos12x + cos10x) – (cos8x+ cos6x)= 0

⇒ 2. cos 11x. cosx – 2cos7x. cos x= 0

⇒ 2cosx. ( cos11x- cos7x)=0

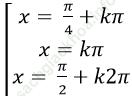
Chọn A.

Câu 12: Giải phương trình: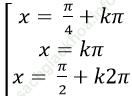

A.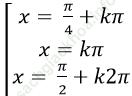

B.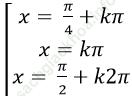

C. I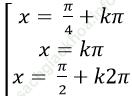

D. Đáp án khác

Hiển thị lời giải

+ Ta có: cosx+ cos2x + cos3x = (cosx+cos 3x) + cos2x

= 2cos 2x. cosx + cos2x = cos2x. (2cosx + 1)

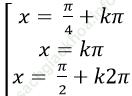
Câu 13: Giải phương trình: sin2x + cosx + 1+ 3sin² x – cos² x + 2sinx= 0

A.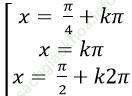

B.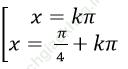

C.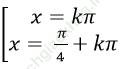

D. Đáp án khác

Hiển thị lời giải

Ta có: sin2x+ cosx + 1+ 3sin2 x –cos2 x+2sinx=0

⇒ (sin2x + 2sinx) + (cosx+ 1) + (3sin2 x – cos2x) = 0

⇒ (2sinx. cosx+ 2sinx) + (cosx+1) + (3sin2 x + sin2 x- 1) = 0

⇒ 2sinx. ( cosx+ 1) + (cosx+ 1) + (4sin2 x -1) = 0

⇒ (2sinx+ 1). (cosx+1) + (2sinx- 1). (2sinx+1) = 0

⇒ (2sinx +1). (cosx+ 1 +2sinx -1) = 0

⇒ (2sinx+1). (cosx+ 2sinx) = 0

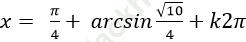
Chọn C.

Câu 14: Phương trình: 5sinx+ 5cosx + sin3x = cos3x + √ 3 (2+ sin2x) có bao nhiêu họ nghiệm?

A. 1

B. 2

C. 3

D. 4

Hiển thị lời giải

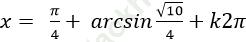
Vậy phương trình đã cho có hai họ nghiệm.

Chọn B.

Câu 15:Giải phương trình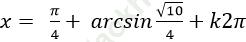

A.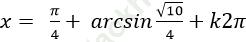

B.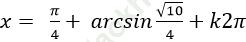

C.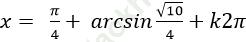

D. Cả A và B đều đúng

Hiển thị lời giải

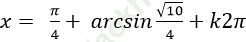
Chọn C.

Bài trước: Phương trình đối xứng, phản đối xứng đối với sinx và cosx - Chuyên đề Toán 11 Bài tiếp: Phương trình lượng giác không mẫu mực - Chuyên đề Toán 11