Cách tính đạo hàm bằng định nghĩa - Chuyên đề Toán 11
A. Phương pháp giải
+ Định nghĩa đạo hàm của hàm số: Cho hàm số y= f (x) xác định trên khoảng (a; b) và x0∈ (a; b). Nếu tồn tại giới hạn hữu hạn:
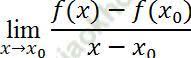
Thì giới hạn đó được gọi là đạo hàm của hàm số y= f (x) tại điểm x0 và kí hiệu:
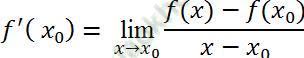
+ Quy tắc tính đạo hàm bằng định nghĩa:
Bước 1: giả sử ∆ x là số gia của đối số x0. Tính ∆ y= f (x0 + ∆x) – f (x0).
Bước 2: Lập tỉ số ∆y/∆x
Bước 3: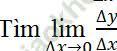
B. Ví dụ minh họa
Ví dụ 1. Giới hạn (nếu tồn tại) nào sau đây dùng để định nghĩa đạo hàm của hàm số y= f (x) tại x0 < 1?
Bài giải:
Theo định nghĩa đạo hàm của hàm số tại một điểm thì biểu thức ở đáp án C đúng.
Đáp án đúng là: C.
Ví dụ 2. Cho hàm số y= f (x) liên tục tại x0. Đạo hàm của hàm số y= f (x) tại x0 là:
Bài giải:
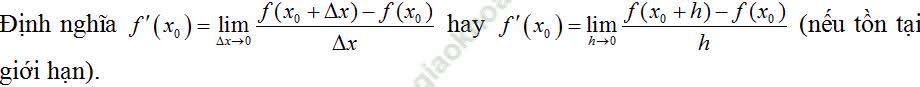
Đáp án đúng là: C.
Ví dụ 3. Số gia của hàm số y = f (x) = x3 + 1 ứng với x0 = 1 và ∆ x = 1 bằng bao nhiêu?
A. – 10 B. 7 C. - 1. D. 0
Bài giải:
Ta có ∆y = f (x0 + ∆x) - f (x0 ) = (x0 + ∆x)3 + 1 - x03 - 1
= 3. x02.∆x + 3x0 (∆x)2 + (∆x)3
Với x0 = 1 và ∆ x = 1 thì ∆ y = 7.
Đáp án đúng là: B
Ví dụ 4. Tỉ số ∆y/∆x của hàm số f (x) = x2 + x theo x và là
A. 2x02 ∆x+1
B. 2x0- ∆x
C. 2x0+ ∆x+1
D. 2x0.∆x+ (∆x)2+1
Bài giải:
Giả sử ∆x là số gia của đối số tại xo. Ta có:
∆ y = f (x0 + ∆x) - f (x0) = (x0 + ∆x)2 + x0 + ∆x - x02 - x0
= x02 + 2x0.∆x + (∆x)2 + x0 + ∆x - x02 - x0
= 2x0.∆x + (∆x)2 + ∆x
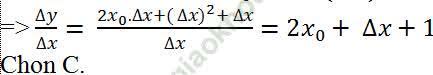
Ví dụ 5. Số gia của hàm số y = f (x) = 2x + 8 ứng với số gia của đối số x tại x0 = 3 là
A. 3
B. 2∆x
C. -2∆x + 3
D. Đáp án khác
Bài giải:
Với số gia của đối số x tại x0 = 3. Ta có:
∆ y = f (x0 + ∆x) - f (x0) = 2 (x0 + ∆x) + 8 - 2x0 - 8 = 2∆x
=> Số gia của hàm số tại x0 = 3 là 2∆x.
Đáp án đúng là: B
Ví dụ 6. Cho hàm số y = x3- 1. Tính ∆ y của hàm số theo x và ∆ x?
A. 3x2.∆ x + 3x. (∆x)2 + (∆x)3
B. x2.∆ x + x. (∆x)2 + (∆x)3
C. 3x2.∆ x + 3x. (∆x)2 + (∆x)3 + 2
D. Đáp án khác
Bài giải:
+ Giả sử ∆ x là số gia của đối số.
+ Ta có; ∆y = f (x + ∆x) - f (x) = (x + ∆x)3 – 1 - x3 + 1
= x3 + 3x2.∆ x + 3x. (∆x)2 + (∆x)3 – x3
= 3x2.∆ x + 3x. (∆x)2 + (∆x)3
Đáp án đúng là: A.
Ví dụ 7. Cho hàm số y = x2 + 2x - 3. Tính tỉ số ∆y/∆x theo x và ∆ x
A. 2x + ∆x - 2
B. 2x + ∆x + 2 (∆)2
C. 2x - ∆x + 2
D. 2x + ∆x + 2
Bài giải:
+ Gọi ∆x là số gia của đối số x.
+ Ta có: ∆ y = f (x + ∆x) – f (x) = [(x + ∆x)2 + 2 (x + ∆x) - 3] – [x2 + 2x - 3]
= x2 + 2x. ∆x + (∆x)2 + 2x + 2. ∆x – 3 – x2 - 2x + 3
= 2x. ∆x + (∆x)2 + 2. ∆x
+ ∆y/∆x = 2x + ∆x + 2
Đáp án đúng là: D.
Ví dụ 8. Cho hàm số y = f (x) = x2 - x, đạo hàm của hàm số ứng với số gia của đối số x tại x0 là:
A. x0+1
B. x0 – 2
C. x0 - 2∆x
D. 2x0 - 1
Bài giải:
Ví dụ 9. Cho hàm số:
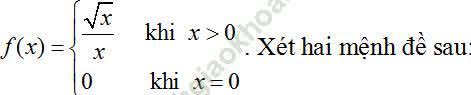
(I). f' (0) = 1
(II) Hàm số không có đạo hàm tại x0 = 0.
Mệnh đề nào đúng?
A. Chỉ (I).
B. Chỉ (II).
C. Cả hai đều sai.
D. Cả hai đều đúng.
Bài giải:
Gọi ∆x là số gia của đối số tại 0 sao cho ∆ x > 0.
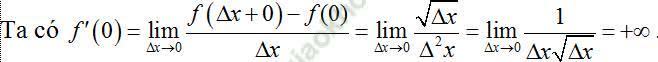
Nên hàm số không có đạo hàm tại 0.
Đáp án đúng là: B.
Ví dụ 10.
Hàm số:
Bài giải:
Ví dụ 11. Cho hàm số y= 8x+ 10. Tính đạo hàm của hàm số tại x0= -1.
A. 6
B. 10
C. 8
D. - 15
Bài giải:
+ Giả sử ∆x là số gia của đối số tại x0 = -1.
∆ y = f (-1 + ∆x) – f (-1) = 8 (- 1 + ∆x) + 10 – [8. (- 1) + 10]
= - 8 + 8∆x + 10 - 2 = 8. ∆x
=> ∆y/∆x = 8 nên: 
Vậy đạo hàm của hàm số đã cho tại điểm x0 = -1 là 8.
Chọn C.
Ví dụ 12. Cho hàm số: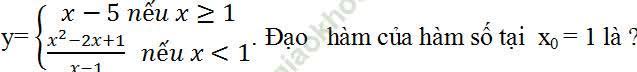 
A. 0 B. 2 C. 1 D. Đáp án khác
Bài giải:
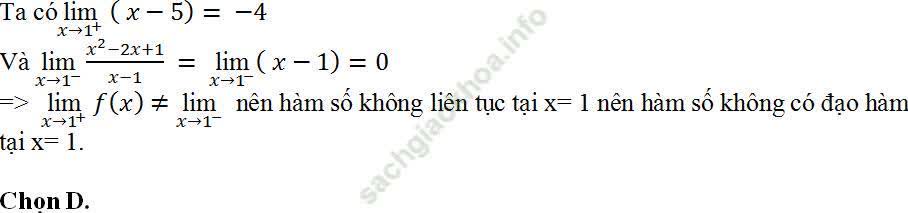
Ví dụ 13. Cho hàm số:
Bài giải:
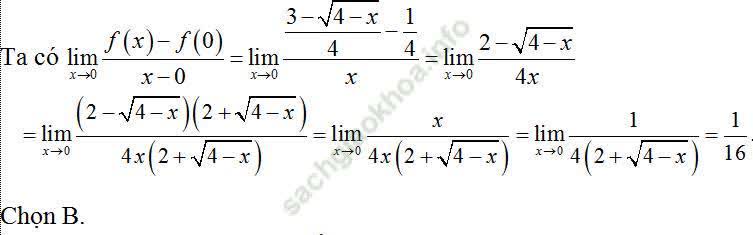
Ví dụ 14. Cho hàm số:
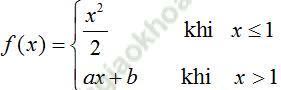
Với giá trị nào của a; b thì hàm số có đạo hàm tại x = 1?
Bài giải:
C. Bài tập vận dụng
Câu 1: Số gia của hàm số y = - 3x2 + 8 ứng với x và là:
A. -6x. ∆x -3 (∆x)2
B. -6x. ∆x+ 3 (∆x)2- 16
C. 6x. ∆x -3 (∆x)2 + 16
D. -6x - 3. ∆x
+ Gọi ∆x là số gia của đối số x.
+ Ta có: ∆ y= f (x+ ∆x) – f (x)= [- 3 (x+∆x)2 +8] – [- 3x2+ 8]
= -3x2 - 6x. ∆x -3 (∆x)2+ 8 + 3x2- 8
= -6x. ∆x -3 (∆x)2
Chọn A.
Câu 2: Xét 3 mệnh đề sau:
(1) Nếu hàm số y = f (x) có đạo hàm tại điểm x = x0 thì hàm số liên tục tại điểm đó.
(2) Nếu hàm số y = f (x) liên tục tại điểm x = x0 thì hàm số y = f (x) có đạo hàm tại điểm đó.
(3) Nếu y = f (x) gián đoạn tại x = x0 thì chắc chắn hàm số y = f (x) không có đạo hàm tại điểm đó.
Trong 3 câu trên:
A. Có hai câu đúng và một câu sai.
B. Có một câu đúng và hai câu sai.
C. Cả ba đều đúng.
D. Cả ba đều sai.
(1) Nếu hàm số y=f (x) có đạo hàm tại điểm x= x0 thì hàm số y= f (x) liên tục tại điểm đó. Đây là mệnh đề đúng.
(2) Nếu hàm số y= f (x) liên tục tại điểm x= x0 thì hàm số y=f (x) có đạo hàm tại điểm đó là mệnh đề sai.
Ví dụ: Lấy hàm ta có D= R nên hàm số y= f (x) liên tục trên R.
Nên hàm số không có đạo hàm tại x= 0.
(3) Nếu hàm số y= f (x) gián đoạn tại x=x0 thì chắc chắn hàm không có đạo hàm tại điểm đó là mệnh đề đúng.
Vì (1) là mệnh đề đúng nên (1) tương đương với mệnh đề sau: Nếu hàm số y=f (x) không liên tục tại x= x0 thì hàm số y= f (x) không có đạo hàm tại điểm đó.
Vậy (3) là mệnh đề đúng.
Chọn A.
Câu 3: Xét 2 câu sau:
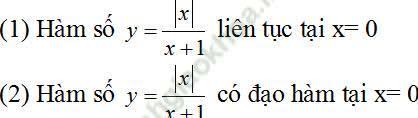
Trong 2 câu trên:
A. Chỉ có (2) đúng.
B. Chỉ có (1) đúng.
C. Cả hai đều đúng.
D. Cả hai đều sai.
Câu 4: Cho hàm số y = x2 + 2|x| - 5. Xét 2 câu sau:
(1). Hàm số trên có đạo hàm tại x = 0.
(2). Hàm số trên liên tục tại x = 0.
Trong 2 câu trên:
A. Chỉ có (1) đúng. B. Chỉ có (2) đúng. C. Cả hai đều đúng. D. Cả hai đều sai.
Câu 5: Tìm a; b để hàm số: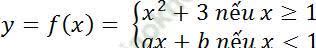 
có đạo hàm tại x = 1.
A. a= - 3; b= 7 B. a= 2; b=2 C. a= 1; b= 3 D. a= 4; b= 0
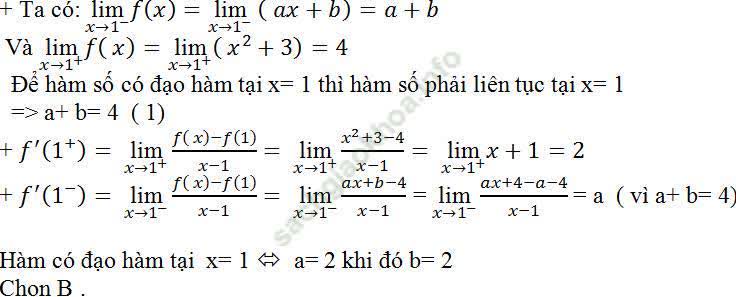
Câu 6: Cho hàm số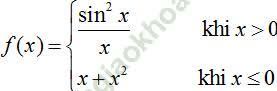 
tính đạo hàm của hàm số tại x0 = 0
A. 1 B. 2 C. 3 D. 5
Ta có: f (0) = 0. Xét các đạo hàm một bên của hàm số:
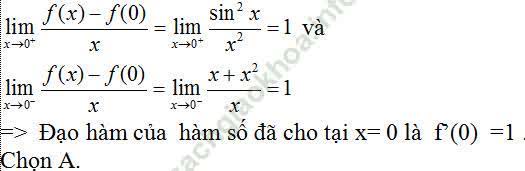
Câu 7: Tính đạo hàm của hàm số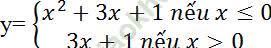 
tại điểm x0 = 0.
A. 2 B. 0 C. 3 D. đáp án khác
Ta có: f (0) = 1. Ta xét các đạo hàm một bên của hàm số:
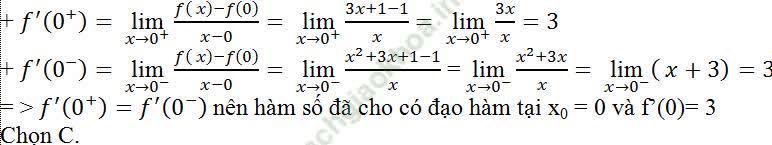
Câu 8: Tính đạo hàm của hàm số y = f (x) = 2x3 + 1 tại các điểm x = 2.
A. 12 B. 16 C. 24 D. 18
Ta có: f (2) = 2.23+ 1= 17
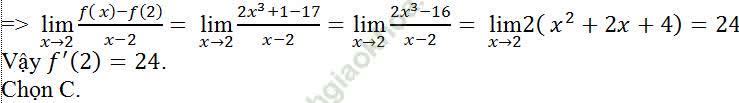
Câu 9: Tính đạo hàm của hàm số y = f (x) = √ (x2+3) tại x = 1
A. 1 B. 1/2 C. 2 D. 1/4
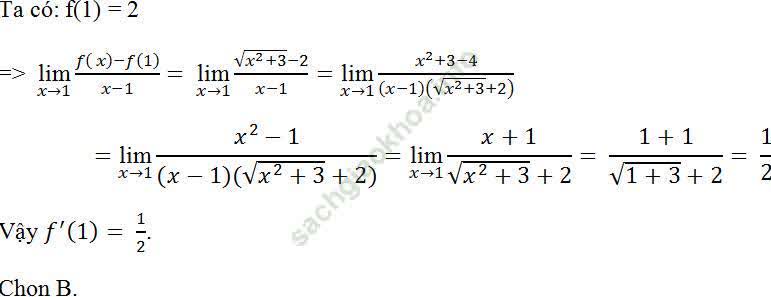
Câu 10: Tính đạo hàm của hàm số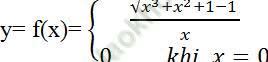 
khi x ≠ 0 tại x = 0
A. 1/2 B. 1 C. 2 D. 1/4
Ta có f (0) = 0
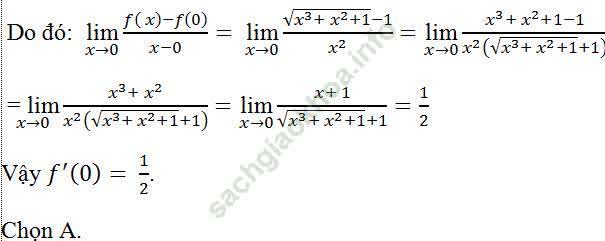
Câu 11: Cho hàm số y = f (x) = (2x2 + |x + 1|)/ (x - 1). Tìm mệnh đề đúng?
A. Hàm số đã cho có đạo hàm tại x= -1.
B. Hàm số đã cho liên tục nhưng không có đạo hàm tại x= -1.
C. Hàm số đã cho không liên tục tại x= -1
D. Hàm số đã cho có đạo hàm tại x= -1 nhưng không liên tục tại điểm đó.
Vì hàm số y= f (x) xác định tại x= -1 nên nó liên tục tại đó.
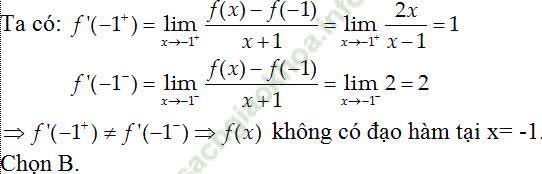
Câu 12: Tìm a để hàm số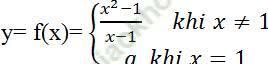 
có đạo hàm tại x=1
A. – 1 B. 1 B. – 2 D. 2
Để hàm số có đạo hàm tại x= 1 thì trước hết hàm số phải liên tục tại x= 1
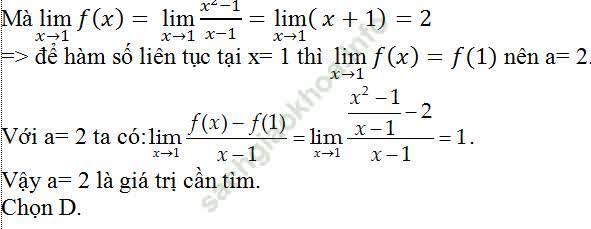
Câu 13: Tính đạo hàm của hàm số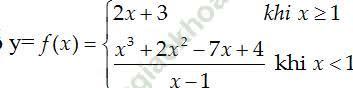 
tại x0= 1.
A. 0 B. 4 C. 5 D. Đáp án khác
Bài giải:
