Cách tìm thiết diện của hình chóp - Chuyên đề Toán 11
A. Phương pháp giải
Thiết diện của hình chóp và mặt phẳng (P) là đa giác giới hạn bởi các giao tuyến của (P) với các mặt hình chóp
Phương pháp: Xác định lần lượt các giao tuyến của (P) với các mặt của hình chóp theo các bước sau:
- Từ điểm chung có sẵn, xác định giao tuyến đầu tiên của (P) với một mặt của hình chóp (Có thể là mặt trung gian)
- Cho giao tuyến này cắt các cạnh của mặt đó của hình chóp ta sẽ được các điểm chung mới của (P) với các mặt khác. Từ đó xác định được các giao tuyến mới với các mặt này
- Tiếp tục như thế cho tới khi các giao tuyến khép kín ta được thiết diện.
B. Ví dụ minh họa
Ví dụ 1: Cho ABCD là một tứ giác lồi và điểm S không thuộc mặt phẳng (ABCD). Hình nào sau đây không thể là thiết diện của hình chóp S. ABCD?
A. Tam giác
B. Tứ giác
C. Ngũ giác
D. Lục giác
Bài giải:
Hình chóp S. ABCD có 5 mặt nên thiết diện của hình chóp có tối đa 5 cạnh
Vậy thiết diện không thể là lục giác
Đáp án cần chọn là: D
Ví dụ 2: Cho hình chóp S. ABCD có đáy ABCD là hình bình hành và điểm M ở trên cạnh SB. Mặt phẳng (ADM) cắt hình chóp theo thiết diện là:
A. tam giác
B. Tứ giác
C. hình bình hành
D. ngũ giác
Bài giải:
+ Trong mặt phẳng (ABCD) gọi O là giao điểm của AC và BD
+ Trong mặt phẳng (SBD) gọi H là giao điểm của SO và DM
+ Trong mặt phẳng (SAC) gọi K là giao điểm của AH và SC
+ Ta tìm giao tuyến của mặt phẳng (ADM) với các mặt của hình chóp:
(ADM) ∩ (SAD) = AD
(ADM) ∩ (SDC) = DK
(ADM) ∩ (SCB) = KM
(ADM) ∩ (SAB) = AM
⇒ Thiết diện của hình chóp cắt bởi mp (ADM) là tứ giác ADKM
Chọn đáp án: B
Ví dụ 3: Cho hình chóp tứ giác S. ABCD, có đáy là hình thang với AD là đáy lớn và P là một điểm trên cạnh SD. Thiết diện của hình chóp cắt bởi mặt phẳng (PAB) là hình gì?
A. Tam giác
B. Tứ giác
C. Hình thang
D. Hình bình hành
Bài giải:
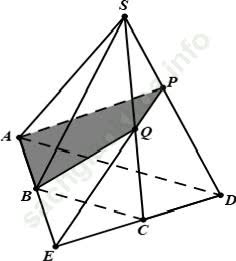
Trong mặt phẳng (ABCD), gọi E = AB ∩ CD
Trong mặt phẳng (SCD) gọi Q = SC ∩ EP
Ta có: E ∈ AB nên EP ⊂ (ABP) ⇒ Q ∈ (ABP), do đó Q = SC ∩ (ABP)
+ Giao tuyến của mặt phẳng (PAB) với các mặt của hình chóp:
(PAB) ∩ (SAB) = AB
(PAB) ∩ (SBC) = BQ
(PAB) ∩ (SCD) = QP
(PAB) ∩ (SAD) = PA
Thiết diện là tứ giác ABQP
Chọn đáp án: B
Ví dụ 4: Cho hình chóp tứ giác S. ABCD, có đáy là hình thang với AD là đáy lớn và P là một điểm trên cạnh SD. Gọi M; N lần lượt là trung điểm của các cạnh AB; BC. Thiết diện của hình chóp cắt bởi (MNP) là hình gì?
A. Ngũ giác
B. Tứ giác
C. Hình thang
D. Hình bình hành
Bài giải:
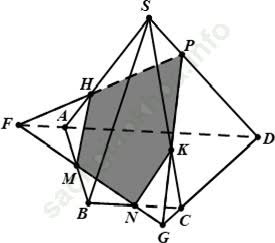
+ Trong mặt phẳng (ABCD) gọi F và G lần lượt là các giao điểm của MN với AD và CD.
+ Trong mặt phẳng (SAD) gọi H = SA ∩ FP
+ Trong mặt phẳng (SCD) gọi K = SC ∩ PG
Ta có F ∈ MN ⇒ F ∈ (MNP)
⇒ FP ⊂ (MNP) ⇒ H ∈ (MNP)
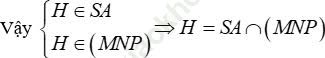
Tương tự K = SC ∩ (MNP)
+ Giao tuyến của mặt phẳng (MNP) với các mặt của hình chóp:
(MNP) ∩ (SAB) = HM
(MNP) ∩ (ABCD) = MN
(MNP) ∩ (SBC) = NK
(MNP) ∩ (SCD) = KP
(MNP) ∩ (SAD) = PH
Vậy thiết diện của hình chóp cắt bởi mp (MNP) là ngũ giác HMNKP
Chọn đáp án: A
Ví dụ 5: Cho tứ diện ABCD; gọi H và K lần lượt là trung điểm của AB và BC. Trên đường thẳng CD lấy điểm M nằm ngoài đoạn CD. Thiết diện của tứ diện cắt bởi mặt phẳng (HKM) là:
A. Tứ giác HKMN với N thuộc AD
B. Hình thang HKMN với N thuộc AD và HK // MN
C. Tam giác HKL với L là giao điểm của KM và BD
D. Tam giác HKT với T là giao điểm của HM và AD
Bài giải:
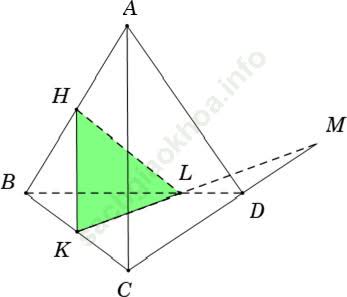
+ Trong mặt phẳng (BCD), do KM không song song với CD nên gọi L là giao điểm của KM và BD.
+ Ta có: (HKM) ∩ (ABC) = HK
(HKM) ∩ (BCD) = KL
(HKM) ∩ (ABD) = HL
Vậy thiết diện là tam giác HKL.
Chọn đáp án: C
Ví dụ 6: Cho hình chóp S. ABCD đáy là hình bình hành tâm O. Gọi M, N, I là ba điểm lấy trên AD, CD, SO. Thiết diện của hình chóp với mặt phẳng (MNI) là?
A. Tam giác
B. Tứ giác
C. Ngũ giác
D. Tam giác hoặc tứ giác
Bài giải:
+ Trong mp (ABCD), gọi J = B ∩ MN
K = MN ∩ AB
H = MN ∩ BC
+ Trong mp (SBD), gọi Q = IJ ∩ SB
+ Trong mp (SAB), gọi R = KQ ∩ SA
+ Trong mp (SBC), gọi P = QH ∩ SC
Vậy: thiết diện là ngũ giác MNPQR
Chọn đáp án: C
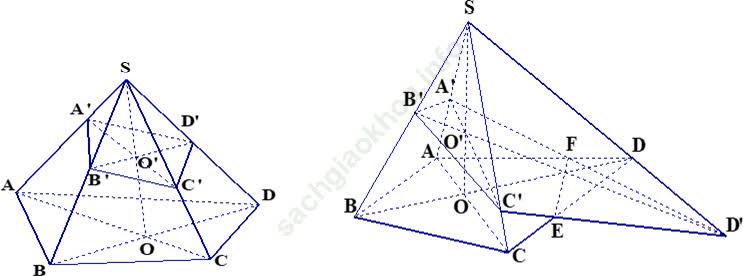
Ví dụ 7: Cho hình chóp S. ABCD hình thang; đáy không là hình thang. Gọi A’, B’, C’ là ba điểm lấy trên các cạnh SA, SB, SC. Thiết diện của hình chóp khi cắt bởi mặt phẳng (A’B’C’) là?
A. Tam giác
B. Tứ giác
C. Ngũ giác
D. Tứ giác hoặc ngũ giác.
Bài giải:
+ Trong mp (ABCD), gọi O = AC ∩ BD
+ Trong mp (SAC), gọi O’ = A’C’ ∩ SO
+ Trong mp (SBD), gọi D’ = B’O’ ∩ SD
Có 2 trường hợp:
• Nếu D’ thuộc cạnh SD thì thiết diện là tứ giác A’B’C’D’
• Nếu D’ thuộc không cạnh SD thì:
Gọi E = CD ∩ C’D’
F = AD ∩ A’D’
⇒ Thiết diện là ngũ giác A’B’C’EF
Chọn đáp án: D
Ví dụ 8: Cho tứ diện đều ABCD có cạnh bằng a. Gọi G là trọng tâm tam giác ABC. Mặt phẳng (GCD) cắt tứ diện theo một thiết diện có diện tích là:

Bài giải:
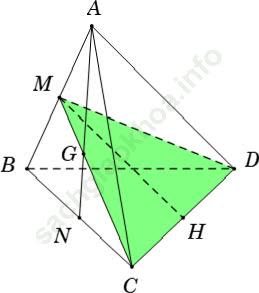
+ Gọi M; N lần lượt là trung điểm của AB; BC
Do G là trọng tâm tam giác ABC nên G là giao điểm AN và CM.
+ Ta thấy mặt phẳng (GCD) cắt đường thẳng AB tại điểm M
⇒ Tam giác MCD là thiết diện của mặt phẳng (GCD) và tứ diện ABCD.
+ Tam giác ABD đều, có M là trung điểm AB => MD = BD. sin 60° = (a√ 3)/2
Tam giác ABC đều, có M là trung điểm AB => MC = BC. sin 60° = (a√ 3)/2
⇒ Tam giác MCD là tam giác cân tại M.
+ Gọi H là trung điểm của CD ⇒ MH ⊥ CD nên SMCD = (1/2)MH. CD
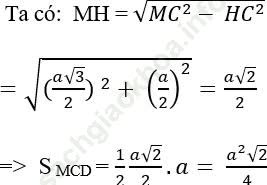
Chọn đáp án là: B
Ví dụ 9: Cho tứ diện đều ABCD có độ dài cạnh bằng 2a. Gọi M; N lần lượt là trung điểm của AC; BC; gọi P là trọng tâm tam giác BCD. Mặt phẳng (MNP) cắt tứ diện theo một thiết diện có diện tích là:

Bài giải:
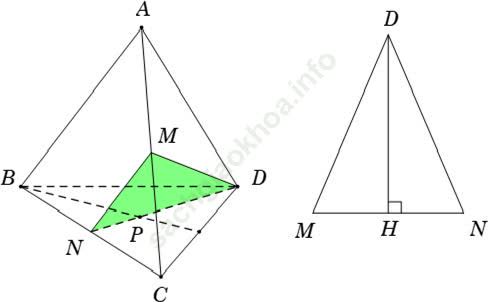
+ Trong tam giác BCD có: P là trọng tâm và N là trung điểm BC
=> 3 điểm N; P; D thẳng hàng
+ Giao tuyến của mặt phẳng (MNP) với mặt phẳng (ABC); mặt phẳng (BCD) và mặt phẳng (ACD) lần lượt là: MN; ND và MD.
⇒ Thiết diện là tam giác MND
+ Xét tam giác MND, ta có MN = AB/2 = a (MN là đường trung bình của tam giác)
Và DM = DN = (AD√ 3)/2 = a√ 3
Do đó tam giác MND cân tại D.
+ Gọi H là trung điểm MN suy ra DH ⊥ MN
Diện tích tam giác:
Chọn đáp án: C
Ví dụ 10: Cho tứ diện ABCD. Gọi M; N lần lượt là trung điểm AB và CD. Mặt phẳng (α) qua MN cắt AD tại P. Thiết diện của hình chóp cắt bởi mp (α) là:
A. Tứ giác
B. Tam giác
C. Ngũ giác
D. Hình bình hành
Bài giải:
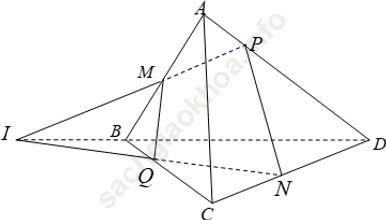
+ Trong mặt phẳng (ABD), gọi giao điểm của MP và BD là I
+ Trong mặt phẳng (BCD), gọi giao điểm của IN và BC là Q
+ Ta có: (α) ∩ (ABD) = PM
(α) ∩ (ABC) = MQ
(α) ∩ (ACD) = NP
(α) ∩ (BCD) = NQ
⇒ Thiết diện cua hình chóp cắt bởi mp (α) là tứ giác MPNQ.
Chọn đáp án: A
C. Bài tập trắc nghiệm
Câu 1: Cho hình chóp S. ABCD với đáy ABCD là tứ giác lồi. Thiết diện của mặt phẳng (α) tuỳ ý với hình chóp không thể là:
A. Lục giác
B. Ngũ giác
C. Tứ giác
D. Tam giác.
Chọn A
Thiết diện của mặt phẳng với hình chóp là đa giác được tạo bởi các giao tuyến của mặt phẳng đó với mỗi mặt của hình chóp
Hai mặt phẳng bất kì có nhiều nhất một giao tuyến.
Hình chóp tứ giác S. ABCD có 5 mặt nên thiết diện của (α) với S. ABCD có không qua 5 cạnh, không thể là hình lục giác 6 cạnh
Câu 2: Cho tứ diện S. ABC. Lấy điểm E; F lần lượt trên đoạn SA; SB và điểm G trọng tâm giác ABC. Gọi H là giao điểm của EF và AB; J là giao điểm của HG và BC. Tìm mệnh đề đúng?
A. Thiết diện của hình chóp cắt bởi mp (EFG) là tứ giác EFIG
B. Thiết diện của hình chóp cắt bởi mp (EFJ) là tứ giác EFJH
C. Thiết diện của hình chóp cắt bởi mp (GJF) là tứ giác EFJI trong đó I là giao điểm của IH và AC
D. Tất cả sai
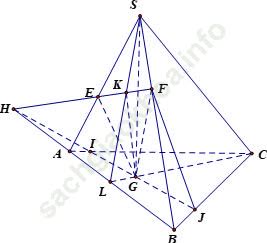
+ Nhận xét: 3 điểm J; G; H thẳng hàng và 3 điểm E, F, H thẳng hàng
Nên 3 mặt phẳng (EFG), (EFJ) và (GJF) là trùng nhau.
Ta xác định thiết diện của hình chóp cắt bởi mặt phẳng (EFG)
+ Trong mp (ABC) gọi I là giao điểm của AC và HJ
⇒ mặt phẳng (EFG) ∩ mp (ABC) = IJ
Mặt phẳng (EFG) ∩ mp (SBC) = JF.
Mặt phẳng (EFG) ∩ mp (SAB) = FE
Mặt phẳng (EFG) ∩ mp (SAC) = EI
⇒ Thiết diện của hình chóp cắt bởi mp (EFG) là tứ giác EFJI.
Chọn C
Câu 3: Cho hình chóp S. ABCD. Điểm A’ nằm trên cạnh SC. Thiết diện của hình chóp với mp (ABA’) là một đa giác có bao nhiêu cạnh?
A. 3 B. 4 C. 5 D. 6
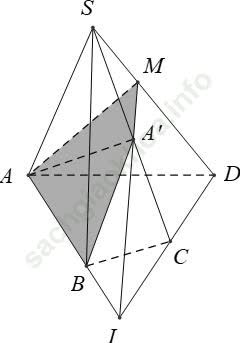
Chọn B
+ Xét (ABA’) và (SCD) có

+ Gọi M = IA' ∩ SD
Có
(ABA') ∩ (SCD) = A'M
(ABA') ∩ (SAD) = AM
(ABA') ∩ (ABCD) = AB
(ABA') ∩ (SBC) = BA'
Thiết diện là tứ giác ABA’M
Câu 4: Cho hình chóp S. ABCD có đáy ABCD là hình bình hành. Gọi I là trung điểm SA. Thiết diện của hình chóp S. ABCD cắt bởi mặt phẳng (IBC) là:
A. Tam giác IBC
B. Hình thang IJCB (J là trung điểm SD)
C. Hình thang IGBC (G là trung điểm SB)
D. Tứ giác IBCD
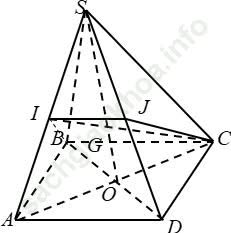
Chọn B
+ Gọi O là giao điểm của AC và BD, G là giao điểm của CI và SO
+ Xét tam giác SAC có Khi đó, G là trọng tâm tam giác SAC. Suy ra G là trọng tâm tam giác SBD
+ Gọi J = BG ∩ SD. Khi đó J là trung điểm SD
+ Do đó thiết điện của hình chóp cắt bởi (IBC) là hình thang IJCB (J là trung điểm SD)
Câu 5: Cho hình chóp S. ABCD có đáy ABCD là một hình bình hành tâm O. Gọi M, N, P là ba điểm trên các cạnh AD, CD, SO. Thiết diện của hình chóp với mặt phẳng (MNP) là hình gì?
A. Ngũ giác B. Tứ giác C. Hình thang D. Hình bình hành
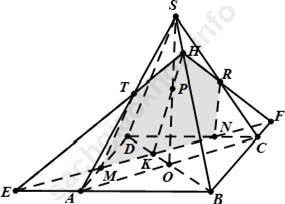
Trong mặt phẳng (ABCD) gọi E, K, F lần lượt là giao điểm của MN với DA, DB, DC
Trong mặt phẳng (SDB) gọi H = KP ∩ SB
Trong mặt phẳng (SAB) gọi T = EH ∩ SA
Trong mặt phẳng (SBC) gọi R = FH ∩ SC

Lí luận tương tự ta có R = SC ∩ (MNP)
Thiết diện là ngũ giác MNRHT
Câu 6: Cho tứ diện ABCD và điểm M thuộc AB và N thuộc CD; điểm G nằm trong tam giác BCD. Tìm thiết diện của hình chóp cắt bởi mp (MNG)?
A. Tam giác MHN với H là giao điểm của NG và BC
B. Tam giác IHN trong đó I là giao điểm của AC và HM
C. Tứ giác MHND với H là giao điểm của NG và BC.
D. Tất cả sai
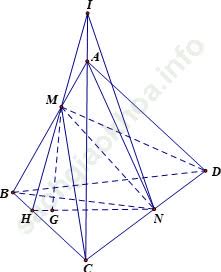
Trong mp (BCD) gọi H là giao điểm của NG và BC
Trong mp (ABC) gọi I là giao điểm của HM và AC
Trong mp (ACD) gọi K là giao điểm của AD và IN
Ta có:
mp (MNG) ∩ mp (BCD) = HN
mp (MNG) ∩ mp (ACD) = NK
mp (MNG) ∩ mp (ABD) = KM
mp (MNG) ∩ mp (ABC) = MH
⇒ Thiết diện của hình chóp cắt bởi mp (MNG) là tứ giác MHNK
Chọn D
Câu 7: Cho hình chóp S. ABCD có đáy là hình bình hành tâm O. Gọi M; N; P lần lượt là trung điểm của các cạnh BC; CD và SA. Tìm mệnh đề đúng về thiết diện của hình chóp cắt bởi (MNP)?
A. Thiết diện là tam giác
B. Thiết diện là tứ giác
C. Thiết diện là ngũ giác
D. Thiết diện là tứ giác hoặc ngũ giác
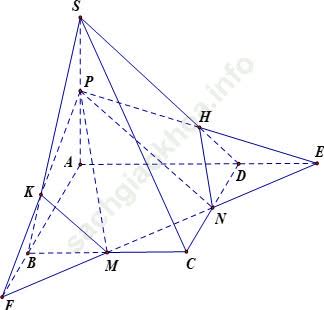
+ Trong mp (ABCD); gọi E là giao điểm của MN và AD
F là giao điểm của MN và AB
+ Trong mp (SAB) gọi K là giao điểm của PF và SB
+ Trong mp (SAD) gọi H là giao điểm của PE và SD
Khi đó:
mp (MNP) ∩ mp (ABCD) = MN
mp (MNP) ∩ mp (SCD) = NH
mp (MNP) ∩ mp (SAD) = HP
mp (MNP) ∩ mp (SAB) = PK
mp (MNP) ∩ mp (SBC) = KM
⇒ Thiết diện của hình chóp cắt bởi mp (MNP) là ngũ giác MNHPK.
Chọn C
Câu 8: Cho hình chóp S. ABCD có đáy ABCD là hình thang, đáy lớn AB. Gọi I, J là trung điểm SA; SB. Lấy điểm M tùy ý trên cạnh SD. Tìm mệnh đề đúng nhất về thiết diện của hình chóp cắt bởi mp (MIJ)
A. Thiết diện là tam giác MIJ
B. Thiết diện là tam giác IJE trong đó E là giao điểm của IM và SH; H là giao điểm của AD và BC.
C. Thiết diện là tứ giác
D. Thiết diện là tam giác hoặc tứ giác
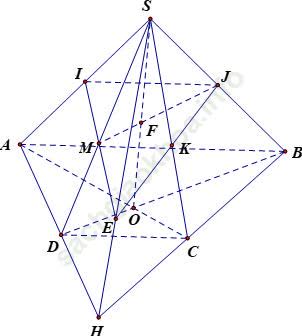
Trong mp (ABCD); gọi H là giao điểm của AD và BC.
Trong mp (SAD); gọi E là giao điểm của IM và SH.
Trong mp (SBC); gọi K là giao điểm của JE và SC.
Ta có:
mp (MIJ) ∩ mp (SAD) = IM
mp (MIJ) ∩ mp (SCD) = MK
mp (MIJ) ∩ mp (SBC) = KJ
mp (MIJ) ∩ mp (SAB) = IJ
⇒ Thiết diện của hình chóp cắt bởi mp (MIJ) là tứ giác IJKM
Chọn C
Câu 9: Cho hình chóp S. ABCD có đáy là hình bình hành ABCD tâm O. Gọi M là trung điểm của SD. Tìm thiết diện của hình chóp cắt bởi mp (BCM)?
A. Tam giác MBC
B. Tứ giác BCME trong đó E là giao điểm của CI và SA, I là giao điểm của SO và BM
C. Tứ giác BCMN trong đó N là giao điểm của BM và SA
D. Đáp án khác
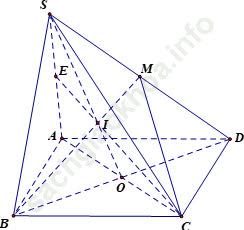
+ Trong mp (SBD); gọi I là giao điểm của SO và BM
+ Trong mp (SAC); gọi E là giao điểm của SA và CI
Khi đó:
mp (BCM) ∩ mp (SBC) = BC
mp (BCM) ∩ mp (SCD) = CM
mp (BCM) ∩ mp (SAD) = ME
mp (BCM) ∩ mp (SAB) = EB
⇒ Thiết diện của hình chóp cắt bởi mp (BCM) là tứ giác BCME
Chọn B