Dạng 1: Viết phương trình tiếp tuyến khi biết tiếp điểm - Chuyên đề Toán 11

A. Phương pháp giải & Ví dụ

- Đường cong (C): y = f (x) có tiếp tuyến tại điểm có hoành độ là x_o khi và chỉ khi hàm số y = f (x) khả vi tại x_o. Trong trường hợp (C) có tiếp tuyến tại điểm có hoành độ x_o thì tiếp tuyến đó có hệ số góc f ’ (x_o)

- Phương trình tiếp tuyến của đồ thị (C): y = f (x) tại điểm M (x_o; f (x_o)) có dạng:

y = f’ (x_o) (x - x_o) + f (x_o)

Bài toán 1. Viết phương trình tiếp tuyến của đồ thị hàm số y = f (x) tại điểm M (x_o; f (x_o))

Bài giải:

Tiếp tuyến của đồ thị hàm số y = f (x) tại M (x_o;f (x_o)) là:

y = f’ (x_o) (x - x_o) + f (x_o) (1)

Bài toán 2. Viết phương trình tiếp tuyến của đồ thị hàm số y = f (x) biết hoành độ tiếp điểm x = x_o

Bài giải:

Tính y_o = f (x_o) và f’ (x_o). Từ đó suy ra phương trình tiếp tuyến:

y = f’ (x_o) (x - x_o) + y_o

Bài toán 3. Viết phương trình tiếp tuyến của đồ thị hàm số y = f (x) biết tung độ tiếp điểm bằng y_o

Bài giải:

Gọi M (x_o, y_o) là tiếp điểm

Giải phương trình f (x) = y_o ta tìm được các nghiệm x_o.

Tính y’ (x_o) và thay vào phương trình (1)

Ví dụ minh họa

Bài 1: Cho hàm số y = x³ + 3x² + 1 có đồ thị là (C). Viết phương trình tiếp tuyến của (C):

1. Tại điểm M (-1; 3)

2. Tại điểm có hoành độ bằng 2

Bài giải:

Hàm số đã cho xác định D = R

Ta có: y’ = 3x² + 6x

1. Ta có: y’ (-1) = -3, khi đó phương trình tiếp tuyến tại M là:

y = -3. (x + 1) + 3 = - 3x

2. Thay x = 2 vào đồ thị của (C) ta được y = 21

Tương tự câu 1, phương trình là:

y = y’ (2). (x – 2) + 21 = 24x – 27

Bài 2: Gọi (C) là đồ thị của hàm số: . Gọi M là một điểm thuộc (C) có khoảng cách đến trục hoành độ bằng 5. Viết phương trình tiếp tuyến của (C) tại M.

Bài giải:

Khoảng cách từ M đến trục Ox bằng 5 ⇔ y_M = ±5.

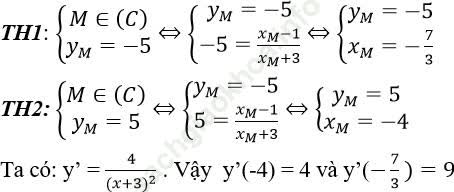
Phương trình tiếp tuyến của (C) tại điểm M (-7/3, -5) là y = 9x + 16

Phương trình tiếp tuyến của (C) tại điểm M (- 4,5) là y = 4x + 21

Bài 3: Cho hàm số y = x³ + 3x² – 6x + 1 (C)

Viết phương trình tiếp tuyến của đồ thị (C) biết hoành độ tiếp điểm bằng 1

Bài giải:

Gọi M (x_o; y_o) là tọa độ tiếp điểm.

Ta có: x_o = 1 ⇒ y_o = - 1

y = x³ + 3x² – 6x + 1 nên y’ = 3x² + 6x – 6.

Từ đó suy ra y’ (1) = 3.

Vậy phương trình tiếp tuyến cần tìm là y = 3 (x – 1) – 1 = 3x – 4

Bài 4: Viết phương trình tiếp tuyến của đồ thị hàm số: y = 2x⁴ – 4x² + 1 biết tung độ tiếp điểm bằng 1

Bài giải:

Gọi M (x_o; y_o) là tọa độ tiếp điểm.

Ta có y_o = 1 ⇒ 2x_o⁴ - 4x_o² + 1 = 1

⇔

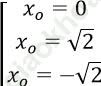
Ta có: y’ = 8x³ – 8x

Với M (0; 1) thì phương trình tiếp tuyến là: y = 0

Với M (√ 2; 1) thì phương trình tiếp tuyến là: y = 8√ 2 (x - √ 2) + 1 = 8√ 2x – 15

Với M (-√ 2; 1) thì phương trình tiếp tuyến là: y = - 8√ 2 (x + √ 2) + 1 = - 8√ 2x – 15

Bài 5: Cho hàm số y = x³ – 3x + 1 (C). Viết phương trình tiếp tuyến của đồ thị (C), biết tiếp điểm là M (0,1).

Bài giải:

y’ = 3x² – 3.

y’ (0) = - 3.

Phương trình tiếp tuyến cần tìm là: y = -3x – 3

Bài 6: Cho hàm số y = x⁴ + x² + 1 (C). Viết phương trình tiếp tuyến của đồ thị (C), biết hoành độ tiếp điểm là nghiệm của phương trình x² = 1.

Bài giải:

Gọi M (x_o; y_o) là tọa độ tiếp điểm.

Ta có: x_o² = 1 ⇔ x_o = ±1

Ta có: y’ = 4x³ + 2x

Với M (1; 3) thì phương trình tiếp tuyến cần tìm là: y = 6 (x – 1) + 3 = 6x – 3

Với M (-1; 3) thì phương trình tiếp tuyến cần tìm là y = -6 (x + 1) + 3 = - 6x – 3

Bài 7: Cho hàm số: . Tìm m để tiếp tuyến của (Cm) tại điểm có hoành độ x_o = 0 đi qua A (4; 3)

Bài giải:

x = 0 ⇒ y = - m – 1

Ta có: . Từ đó => y’ (0) = - m – 3

Phương trình tiếp tuyến tại (0; - m – 1) là: y = (- m – 3)x – m – 1.

Tiếp tuyến đi qua A (4; 3) nên ta có: 3 = 4 (- m – 3) – m – 1 ⇔ m = 16/5

B. Bài tập vận dụng

Bài 1: Cho hàm số y = f (x), có đồ thị (C) và điểm M_o(x_o; f (x_o)) ∈ (C). Phương trình tiếp tuyến của (C) tại M_o là:

A. y = f' (x)(x-x_o)+y_o

B. y = f' (x_o) (x-x_o)

C. y - y_o = f' (x_o) (x-x_o)

D. y - y_o = f' (x_o)x

Hiển thị đáp án

Đáp án: C

Chọn C

Bài 2: Phương trình tiếp tuyến của đồ thị hàm số y = (x + 1)²(x – 2) tại điểm có hoành độ x = 2 là:

A. y = - 8x + 4

B. y = 9x + 18

C. y = -4x + 4

D. y = 9x – 18

Hiển thị đáp án

Đáp án: D

Chọn D.

Gọi M (x_o; y_o) là tọa độ tiếp điểm.

Ta có x_o = 2 ⇒ y_o = 0.

y = (x + 1)²(x – 2) = x³ – 3x – 3 nên y’ = 3x² – 3

Từ đó suy ra y’ (2) = 9

Vậy phương trình tiếp tuyến cần tìm là y = 9 (x – 2) = 9x – 18

Bài 3: Phương trình tiếp tuyến của đồ thị của hàm số y = x (3 – x)² tại điểm có hoành độ x = 2 là

A. y = -3x + 8

B. y = -3x + 6

C. y = 3x – 8

D. y = 3x – 6

Hiển thị đáp án

Đáp án: A

Chọn A.

Gọi M (x_o; y_o) là tọa độ tiếp điểm.

Ta có x_o = 2 ⇒ y_o = 2

y = (3 – x)²x = x³ – 6x² + 9x nên y’ = 3x² – 12x + 9

Từ đó suy ra y’ (2) = - 3

Vậy phương trình tiếp tuyến cần tìm là y = -3 (x – 2) + 2 = -3x + 8

Bài 4: Cho đường cong (C): y = x². Phương trình tiếp tuyến của (C) tại điểm M (-1; 1) là

A. y = -2x + 1.

B. y = 2x + 1.

C. y = -2x - 1.

D. y = 2x – 1.

Hiển thị đáp án

Đáp án: C

Chọn C.

Ta có y = x² nên y’ = 2x

Từ đó suy ra y’ (-1) = -2

Vậy phương trình tiếp tuyết cần tìm là: y = -2 (x + 1) +1 = -2x – 1

Bài 5: Cho hàm số: . Phương trình tiếp tuyến tại A (1; -2) là:

A. y = - 4 (x – 1) – 2

B. y = - 5 (x – 1) + 2

C. y = - 5 (x – 1) – 2

D. y = -3 (x – 1) – 2

Hiển thị đáp án

Đáp án: C

Chọn C.

Ta có

Phương trình tiếp tuyến cần tìm: y = -5 (x – 1) – 2 = -5x + 3

Bài 6: Cho hàm số: . Phương trình tiếp tuyến tại A (0; 2) là:

A. y = 7x + 2

B. y = 7x - 2

C. y = - 7x + 2

D. y = - 7x - 2

Hiển thị đáp án

Đáp án: A

Chọn A.

Ta có: y’ = x² – 6x + 7

Hệ số góc tiếp tuyến y’ (0) = 7

Phương trình tiếp tuyến tại A (0; 2): y = 7x + 2.

Bài 7: Gọi (P) là đồ thị của hàm số y = 2x² – x + 3. Phương trình tiếp tuyến với (P) tại điểm mà (P) cắt trục tung là:

A. y = - x + 3

B. y = - x - 3

C. y = 4x – 1

D. y = 11x + 3

Hiển thị đáp án

Đáp án: A

Chọn A.

Ta có: (P) cắt trục tung tại điểm M (0; 3)

y’ = 4x – 1

Hệ số góc tiếp tuyến: y’ (0) = - 1

Phương trình tiếp tuyến của đồ thị (P) tại M (0; 3) là y = -x + 3

Bài 8: Đồ thị (C) của hàm số: cắt trục tung tại điểm A. Tiếp tuyến của (C) tại điểm A có phương trình là:

A. y = - 4x – 1.

B. y = 4x – 1.

C. y = 5x – 1.

D. y = - 5x – 1.

Hiển thị đáp án

Đáp án: A

Chọn A.

Ta có: điểm A (0; -1)

⇒ hệ số góc của tiếp tuyến y’ (0) = -4

Phương trình tiếp tuyến của đồ thị (C) tại điểm A (0; -1) là:

y = -4x – 1

Bài 9: Cho hàm số: có đồ thị là (H). Phương trình tiếp tuyến tại giao điểm của (H) với trục hoành là:

A. y = 2x – 4.

B. y = 3x + 1.

C. y = - 2x + 4.

D. y = 2x.

Hiển thị đáp án

Đáp án: C

Chọn C

Giao điểm của (H) với trục hoành là A (2; 0). Ta có:

Phương trình tiếp tuyến cần tìm là y = -2 (x – 2) = -2x + 4

Bài 10: Phương trình tiếp tuyến của đồ thị hàm số f (x) = x³ – 2x² + 3x tại điểm có hoành độ x_o = -1 là:

A. y = 10x + 4

B. y = 10x – 5

C. y = 2x – 4

D. y = 2x – 5

Hiển thị đáp án

Đáp án: A

Chọn A.

Tập xác định: D = R

Đạo hàm: y’ = 3x² – 4x + 3

y’ (-1) = 10, y (-1) = - 6

Phương trình tiếp tuyến cần tìm là (d): y = 10 (x + 1) – 6 = 10x + 4

Bài 11: Gọi (H) là đồ thị hàm số: . Phương trình tiếp tuyến của đồ thị (H) tại các giao điểm của (H) với hai trục toạ độ là:

A. y = x – 1

C. y = - x + 1

D. y = x + 1

Hiển thị đáp án

Đáp án: A

Chọn A.

Tập xác định: D = R\ {0}

Đạo hàm: y’ = 1/x²

(H) cắt trục hoành tại điểm có hoành độ là x = 1 và không cắt trục tung

Ta có y’ (1) = 1

Phương trình tiếp tuyến cần tìm là d: y = x – 1

Bài 12: Lập phương trình tiếp tuyến của đồ thị (H): tại giao điểm của (H) và trục hoành:

A. y = (1/3)(x-1)

B. y = 3x

C. y = x – 3

D. y = 3 (x – 1)

Hiển thị đáp án

Đáp án: A

Chọn A

Tập xác định: D = R\ {-2}

Đạo hàm:

(H) cắt trục hoành tại điểm có hoành độ x_o = 1 nên suy ra y’ (1) = 1/3 và y (1) = 0

Phương trình tiếp tuyến cần tìm là d: y = (1/3)(x-1)

Bài 13: Gọi (P) là đồ thị hàm số y = x² – x + 3. Phương trình tiếp tuyến với (P) tại giao điểm của (P) và trục tung là

A. y = -x + 3

B. y = -x - 3

C. y = x - 3

D. y = -3x + 1

Hiển thị đáp án

Đáp án: A

Chọn đáp án A

Tập xác định: D = R

Giao điểm của (P) và trục tung là M (0; 3)

Đạo hàm: y’ = 2x – 1 suy ra hệ số góc của tiếp tuyến tại x = 0 là – 1

Phương trình tiếp tuyến tại M (0; 3) là y = -x + 3.

Bài 14: Tiếp tuyến của đồ thị hàm số: tại điểm có hoành độ x_o = -1 có phương trình là:

A. y = - x + 2

B. y = x + 2

C. y = x – 1

D. y = - x – 3

Hiển thị đáp án

Đáp án: D

Chọn đáp án D.

Tập xác định: D = R\ {1}

Đạo hàm:

Tiếp tuyến tại M (-1; -2) có hệ số góc là k = -1

Phương trình của tiếp tuyến là y = -x – 3

Bài 15: Phương trình tiếp tuyến của đồ thị hàm số y = x⁴ + 2x² – 1 tại điểm có tung độ tiếp điểm bằng 2 là:

A. y = 8x – 6, y = -8x – 6

B. y = 8x – 6, y = -8x + 6

C. y = 8x – 8, y = -8x + 8

D. y = 40x – 57

Hiển thị đáp án

Đáp án: A

Chọn đáp án A

Tập xác định: D = R

Đạo hàm: y’ = 4x³ + 4x

Tung độ tiếp điểm bằng 2 nên 2 = x⁴ + 2x² – 1 ⇔

Tại M (1; 2). Phương trình tiếp tuyến là y = 8x – 6

Tại N (-1; 2). Phương trình tiếp tuyến là y = -8x – 6

Bài tiếp: Dạng 2: Viết phương trình tiếp tuyến khi biết hệ số góc - Chuyên đề Toán 11