Dạng 2: Tìm giới hạn hàm số dạng 0/0, dạng vô cùng trên vô cùng - Chuyên đề Toán 11
A. Phương pháp giải & Ví dụ
Tìm 
trong đó: f (x0) = g (x0) = 0
Dạng này ta gọi là dạng vô định 0/0
Để khử dạng vô định này ta sử dụng định lí Bơzu cho đa thức:
Nội dung định lí: Nếu đa thức f (x) có nghiệm x = x0 thì ta có: f (x) = (x - x0)f1(x)
* Nếu f (x) và g (x) là các đa thức thì ta phân tích
f (x) = (x-x0)f1(x)và: g (x) = (x-x0)g1(x).
Khi đó: 
, nếu giới hạn này có dạng 0/0 thì ta tiếp tục quá trình như trên.
Ví dụ minh họa
Bài 1: Tìm các giới hạn sau: 
Bài giải:
Ta có: 
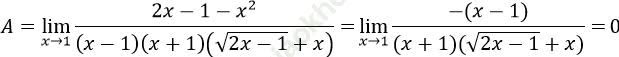
Bài 2: Tìm giới hạn sau: 
Bài giải:
Ta có: 
Bài 3: 
Bài giải:
Đặt t = x - 1 ta có:
Bài 4:
Bài giải:
Ta có:
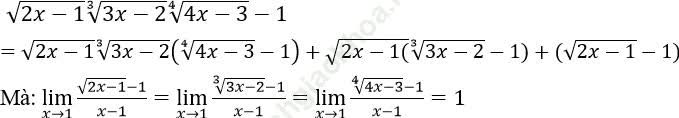
Nên ta có B = 1 + 1 + 1 = 3
Bài 5:
Bài giải:
Ta có:
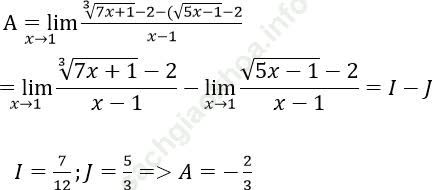
Vậy A = -2/3
Bài 6: Tính 
Bài giải:
Ta có: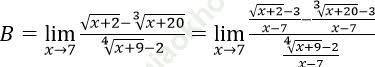 
Mà:
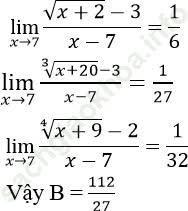
B. Bài tập vận dụng
Bài 1: 
bằng số nào sau đây?
Đáp án: A
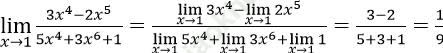
Đáp án là A
Bài 2: 
bằng:
A. 5 B. 1 C. 5/3 D. -5/3
Đáp án: C
Đáp án là C
Bài 3: 
bằng:
A. 0 B. 4/9 C. 3/5 D. +∞
Đáp án: C
Chia cả tử và mẫu của phân thức cho x4 ta có
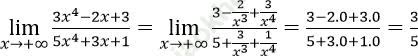
Đáp án C
Bài 4: 
bằng:
A. -2
B. -1
C. 1
D. 2
Đáp án: B
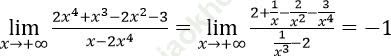
Đáp án là B
Bài 5: 
bằng:
A. -∞ B. 3/5 C. -2/5 D. 0
Đáp án: D
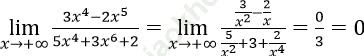
Đáp án là D
Bài 6: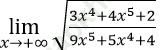 
bằng:
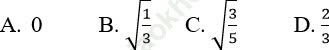
Đáp án: D
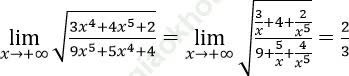
Đáp án là D
Bài 7: 
bằng:
A. -3
B. -1
C. 0
D. 1
Đáp án: A
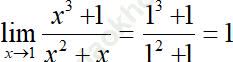
Đáp án là A
Bài 8: 
bằng:
A. -2/3 B. -1/3 C. 0 D. 1/3
Đáp án: B
Đáp án là B
Bài 9: 
bằng:
A. +∞
B. 4
C. 0
D. -∞
Đáp án: C
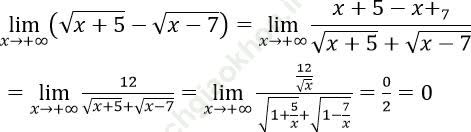
Đáp án C
Bài 10: 
bằng:
A. 0 B. -1 C. -1/2 D. -∞
Đáp án: A
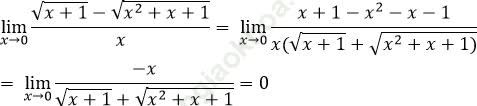
Đáp án A
Bài 11: 
bằng:
A. 1/4 B. 1/6 C. 1/8 D. -1/8
Đáp án: C
Đáp án C
Bài 12: 
bằng:
A. +∞ B. 1/8 C. -9/8 D. -∞
Đáp án: D
Tử số có giới hạn là -1, mẫu số có giới hạn là 0 và khi x < -2 thì x2 + 2x > 0. Do đó
Đáp án D
Bài 13: 
bằng:
A. 0 B. -1/6 C. -1/2 D. -∞
Đáp án: A
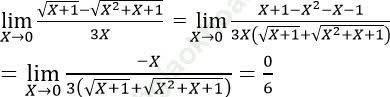
Đáp án A
Bài 14: 
bằng:
A. +∞ B. 2/5 C. -7 D. -∞
Đáp án: C
Đáp án C
Bài 15: 
bằng:
A. 2/3 B. 1/2 C. -2/3 D. -1/2
Đáp án: C
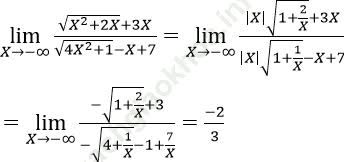
Đáp án C