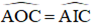Luyện tập trang 83 SGK Toán 9 Tập 2
Bài 39 trang 83 SGK Toán 9 Tập 2:
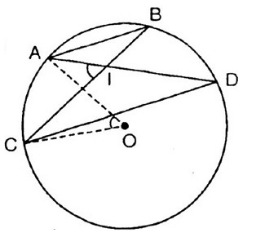
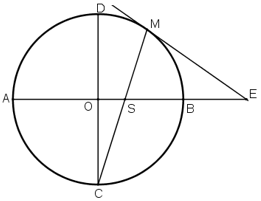
Cho AB và CD là hai đường kính vuông góc của đường tròn (O). Trên cung nhỏ BD lấy một điểm M. Tiếp tuyến tại M cắt tia AB ở E, đoạn thẳng CM cắt AB ở S.
Chứng minh: ES = EM.
Hướng dẫn giải:
Ta có hình vẽ như sau:
+ Số đo của góc có đỉnh bên trong đường tròn bằng một nửa tổng số đo của hai cung bị chắn.
+ Số đo của góc tạo bởi tiếp tuyến và dây cung bằng một nửa số đo của cung bị chắn.
Bài 40 trang 83
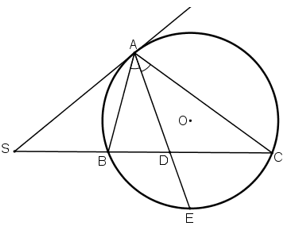
Tia phân giác AD cắt (O) tại E.
+ 
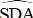là góc có đỉnh nằm bên trong đường tròn
+ 
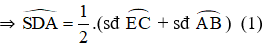
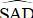là góc tạo bởi tiếp tuyến AS và dây AE
+ 
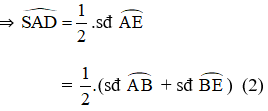
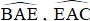lần lượt là các góc nội tiếp chắn các cung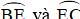 
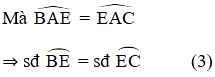
Từ (1); (2) và (3) suy ra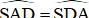 
⇒ ΔSAD cân tại S
⇒ SA = SD (đpcm)
+ Số đo của góc có đỉnh ở bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn.
+ Số đo của góc tạo bởi tiếp tuyến và dây cung bằng nửa số đo cung bị chắn.
+ Các góc nội tiếp bằng nhau chắn các cung bằng nhau.
Bài 41 trang 83:
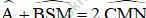
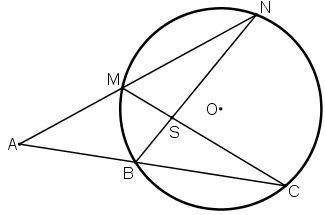
+ Số đo của góc có đỉnh nằm bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn.
+ Số đo của góc có đỉnh nằm bên ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn.
Bài 42 trang 83:
a) Chứng minh AP ⊥ QR.
b) AP cắt CR tại I. Chứng minh tam giác CPI là tam giác cân.
Hướng dẫn giải:
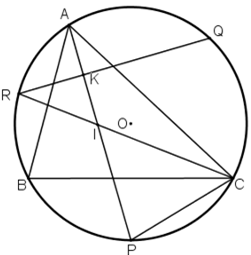
a) Gọi K là giao điểm của QR và AP.
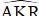là góc có đỉnh K nằm bên trong đường tròn
⇒ AP ⊥ QR (đpcm)
+ R, P lần lượt là điểm chính giữa các cung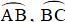 
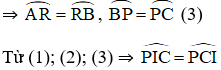
⇒ ΔPCI cân tại P (đpcm).
+ Số đo của góc có đỉnh nằm bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn.
+ Số đo của góc nội tiếp bằng một nửa số đo cung bị chắn.
Bài 43 trang 83:
