Bài 7: Tứ giác nội tiếp - trang 87 Toán 9 Tập 2
Bài 7: Tứ giác nội tiếp
Trả lời câu hỏi Toán 9 Tập 2 Bài 7 trang 87:
a) Vẽ một đường tròn tâm O rồi vẽ một tứ giác có tất cả các đỉnh nằm trên đường tròn đó.
b) Vẽ một đường tròn tâm I rồi vẽ một tứ giác có ba đỉnh nằm trên đường tròn đó còn đỉnh thức tư thì không.
Hướng dẫn giải: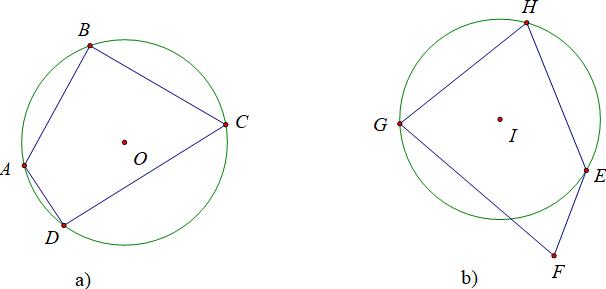
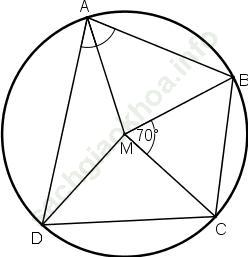
Trả lời câu hỏi Toán 9 Tập 2 Bài 7 trang 88: Xem hình 45. Hãy chứng minh định lý trên.
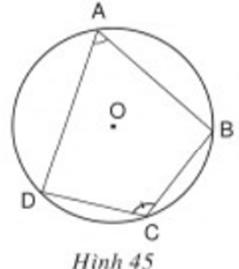
Hướng dẫn giải:
Theo tính chất góc nội tiếp chắn cung, ta có:
∠ (BAD) = 1/2 sđ BCD
∠ (BCD) = 1/2 sđ BAD
⇒ ∠ (BAD) + ∠ (BCD) = 1/2 (sđ BCD + sđ BAD) = 1/2.360o = 180o
Vậy ∠ (BAD) + ∠ (BCD) = 180o
Vậy trong một tứ giác nội tiếp, tổng số đo hai góc đối nhau bằng 180o
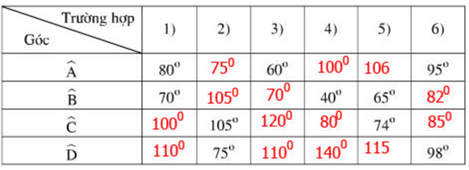
Bài 53 trang 89 SGK Toán 9 Tập 2:
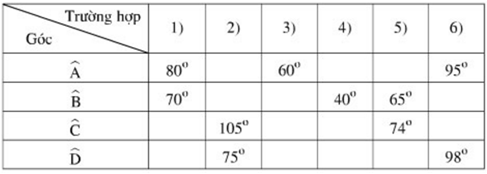
Hướng dẫn giải:
Tứ giác nội tiếp có tổng hai góc đối bằng 180o nên:
- Điền vào ô trống ta có bảng sau:
- Cách tính:


Trong một tứ giác nội tiếp, tổng số đo hai góc đối nhau bằng 180º.
Bài 54 trang 89:
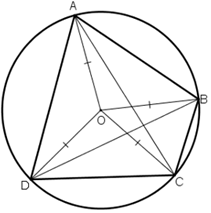
Tứ giác ABCD có ![]()
⇒ ABCD là tứ giác nội tiếp
Gọi O là tâm đường tròn ngoại tiếp tứ giác ABCD
⇒ OA = OB = OC = OD = R
Do OA= OC nên ΔOAC cân tại O, đường trung tuyến kẻ từ O cũng chính là đường cao của tam giác. Suy ra, O thuộc đường trung trực của AC.
Do OB= OD nên ΔOBD cân tại O, đường trung tuyến kẻ từ O cũng chính là đường cao của tam giác. Suy ra, O thuộc đường trung trực của BD
Do OA= OB nên ΔOAB cân tại O, đường trung tuyến kẻ từ O cũng chính là đường cao của tam giác. Suy ra, O thuộc đường trung trực của AB.
⇒ O thuộc đường trung trực của AC, BD, AB.
Vậy các đường trung trực của AC, BD, AB cùng đi qua O. (đpcm)
+ Nếu một tứ giác có tổng số đo hai góc đối nhau bằng 180º thì tứ giác đó nội tiếp một đường tròn.
Bài 55 trang 89: Cho ABCD là một tứ giác nội tiếp đường tròn tâm M, biết:
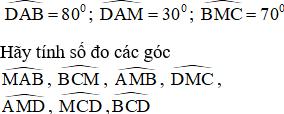
Hướng dẫn giải: