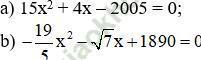Luyện tập trang 49-50 SGK Toán 9 Tập 2
Bài 20 trang 49 SGK Toán 9 Tập 2: Giải các phương trình:
a) 25x2 – 16 = 0;
b) 2x2 + 3 = 0;
c) 4,2x2 + 5,46x = 0;
d) 4x2 - 2√3. x = 1 - √3.
Hướng dẫn giải:
Phương trình vô nghiệm vì x2 ≥ 0 với mọi x.
c) 4,2x2 + 5,46x = 0
⇔ x. (4,2x + 5,46) = 0
⇔ x = 0 hoặc 4,2x + 5,46 = 0
+ Nếu 4,2x + 5,46 = 0
⇔ 
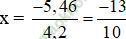
Vậy phương trình có hai nghiệm x1 = 0 và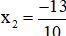 
d) 4x2 - 2√3 x = 1 - √3.
⇔ 4x2 - 2√3 x – 1 + √3 = 0
Có a = 4; b’ = -√3; c = -1 + √3;
Δ’ = b'2 – ac = (-√3)2 – 4 (-1 + √3) = 7 - 4√3 = 4 – 2.2.√3 + (√3)2 = (2 - √3)2.
Phương trình có hai nghiệm phân biệt:
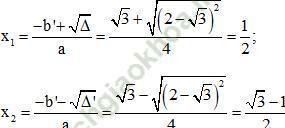
Cách 2: Sử dụng công thức nghiệm thu gọn với a, b, c
Phương trình ax2 + bx + c = 0 (a ≠ 0) có biệt thức Δ = b2 – 4ac.
+ Nếu Δ > 0, phương trình có hai nghiệm phân biệt
+ Nếu Δ = 0, phương trình có nghiệm kép
;+ Nếu Δ < 0, phương trình vô nghiệm.
Bài 21 trang 49: Giải vài phương trình của An Khô-va-ri-zmi (xem Toán 7, Tập 2, tr. 26):
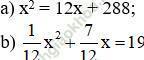
Hướng dẫn giải:
a) x2 = 12x + 288
⇔ x2 – 12x – 288 = 0
Có a = 1; b’ = -6; c = -288; Δ’ = b’2 – ac = (-6)2 – 1. (-288) = 324 > 0
Phương trình có hai nghiệm:
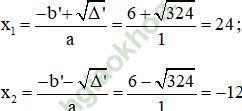
Vậy phương trình có hai nghiệm x1 = 24 và x2 = -12.
b)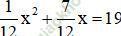 
⇔ x2 + 7x = 228
⇔ x2 + 7x – 228 = 0
Có a = 1; b = 7; c = -228; Δ = b2 – 4ac = 72 – 4.1. (-228) = 961 > 0
Phương trình có hai nghiệm:
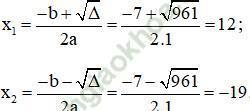
Vậy phương trình có hai nghiệm x1 = 12 và x2 = -19.
Phương trình: ax2 + bx + c = 0 (a ≠ 0) có biệt thức Δ = b2 – 4ac.
+ Nếu Δ > 0, phương trình có hai nghiệm phân biệt
+ Nếu Δ = 0, phương trình có nghiệm kép 
;
+ Nếu Δ < 0, phương trình vô nghiệm.
* Đôi nét về nhà toán học An-khô-va-ri-zmi (Muhammad inb Musa al – Khwarizmi)
- An-khô-va-ri-zmi (780 – 850) là nhà toán học nổi tiếng người Trung Á.
- Năm 820, ông viết một cuốn sách về Toán học, tên cuốn sách được dịch sang tiếng Anh với tiêu đề Algebra (dịch tiếng Việt là Đại số).
- Ông được biết đến như là cha đẻ của môn Đại số. Ông dành cả đời mình nghiên cứu về đại số và đã có nhiều phát minh quan trọng trong lĩnh vực toán học.
- Ngoài ra, ông cũng là nhà thiên văn học, địa lý học nổi tiếng và đóng góp một phần quan trọng trong việc vẽ bản đồ thế giới thời bấy giờ.
Bài 22 trang 49: Không giải phương trình, hãy cho biết mỗi phương trình sau có bao nhiêu nghiệm?
Hướng dẫn giải:
a) Phương trình: 15x2 + 4x – 2005 = 0
Có a = 15; c = -2005 trái dấu
⇒ Phương trình có hai nghiệm phân biệt.
b) Phương trình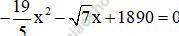 
có 
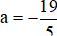; c = 1890 trái dấu
⇒ Phương trình có hai nghiệm phân biệt.
Kiến thức áp dụng
Phương trình ax2 + bx + c = 0 (a ≠ 0) có a và c trái dấu, tức là a. c < 0 thì phương trình luôn có hai nghiệm phân biệt. (Chú ý trang 45 SGK).
Bài 23 (trang 50): Rada của một máy bay trực thăng theo dõi chuyển động của ôtô trong 10 phút, phát hiện rằng vận tốc v của ôtô thay đổi phụ thuộc vào thời gian bởi công thức:
v = 3t2 -30t + 135 (t tính bằng phút, v tính bằng km/h)
a) Tính vận tốc của ôtô khi t = 5 phút.
b) Tính giá trị của t khi vận tốc ôtô bằng 120km/h (làm tròn kết quả đến chữ số thập phân thứ hai).
Hướng dẫn giải:a) Tại t = 5, ta có: v = 3.52 – 30.5 + 135 = 60 (km/h)
b) Khi v = 120 km/h
⇔ 3t2 – 30t + 135 = 120
⇔ 3t2 – 30t + 15 = 0
Có a = 3; b’ = -15; c = 15; Δ’ = b’2 – ac = (-15)2 – 3.15 = 180
Phương trình có hai nghiệm phân biệt
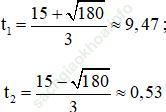
Vì rada quan sát chuyển động của ô tô trong 10 phút nên t1 và t2 đều thỏa mãn.
Vậy tại t = 9,47 phút hoặc t = 0,53 phút thì vận tốc ô tô bằng 120km/h.
Bài 24 trang 50: Cho phương trình (ẩn x): x2 – 2 (m – 1)x + m2 = 0.
a) Tính Δ'.
b) Với giá trị nào của m thì phương trình có hai nghiệm phân biệt? Có nghiệm kép? Vô nghiệm.
Hướng dẫn giải:
a) Phương trình x2 – 2 (m – 1)x + m2 = 0 (1)
Có a = 1; b’ = - (m – 1); c = m2
⇒ Δ’ = b'2 – ac = (1 – m)2 – 1. m2 = 1 – 2m + m2 – m2 = 1 – 2m.
b) Phương trình (1):
+ Vô nghiệm ⇔ Δ’ < 0 ⇔ 1 – 2m < 0 ⇔ 2m > 1 ⇔ m > 
+ Có nghiệm kép ⇔ Δ’ = 0 ⇔ 1 – 2m = 0 ⇔ m =
+ Có hai nghiệm phân biệt ⇔ Δ’ > 0 ⇔ 1 – 2m > 0 ⇔ 2m < 1 ⇔ m <
Vậy: Phương trình (1) có hai nghiệm phân biệt khi m < ; có nghiệm kép khi m = và vô nghiệm khi m >
Phương trình ax2 + 2b’x + c = 0 (a ≠ 0) có biệt thức Δ ’ = b’2 – ac.
+ Nếu Δ ’ > 0, phương trình có hai nghiệm phân biệt
+ Nếu Δ ’ = 0, phương trình có nghiệm kép;
+ Nếu Δ ’ < 0, phương trình vô nghiệm.