Luyện tập trang 15-16 (Tập 2) - SGK Toán 9 Tập 2
Bài 15 trang 15 SGK Toán 9 Tập 2
Giải hệ phương trình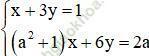 
trong mỗi trường hợp sau:
a) a = -1; b) a = 0; c) a = 1.
Hướng dẫn giải:
Có 2 cách để giải hệ phương trinh trên. Cụ thể:
Cách 1:
Ta có: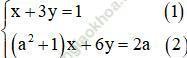 
Từ (1) rút ra được x = 1 – 3y (*)
Thay vào phương trình (2) ta được:
(a2 + 1). (1 – 3y) + 6y = 2a
⇔ a2 + 1 – 3 (a2 + 1)y + 6y = 2a
⇔ a2 +1- 2a = 3a2. y – 6y + 3y
⇔ (a- 1)2 = 3a2y – 3y
⇔ 3 (a2 – 1).y = (a – 1)2 (**)
a) a = -1, phương trình (**) trở thành: 0y = 4
Phương trình trên vô nghiệm
Vậy hệ phương trình khi a = -1 vô nghiệm.
b) a = 0, phương trình (**) trở thành -3y = 1 ⇔ 
Thay vào (*) ta được x = 2.
Vậy hệ phương trình khi a = 0 có nghiệm duy nhất 
c) a = 1, phương trình (**) trở thành: 0y = 0
Phương trình nghiệm đúng với mọi y.
Vậy hệ phương trình khi a = 1 có vô số nghiệm dạng (1 – 3y; y) (y ∈ R).
Cách 2:
a) Thay a = -1 vào hệ phương trình ta được hệ phương trình mới:
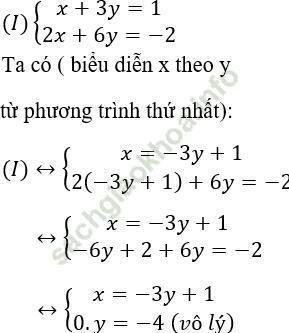
Vậy hệ phương trình vô nghiệm khi a= - 1.
b) Thay a = 0 vào hệ phương trình ta được hệ phương trình mới:
c) Thay a = 1 vào hệ phương trình ta được hệ phương trình mới:
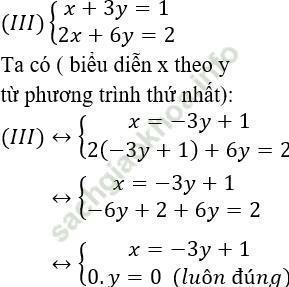
Vậy với a = 1 hệ phương trình có vô số nghiệm với nghiệm tổng quát là (-3y+1; y), (y ∈ R)
Kiến thức áp dụngGiải hệ phương trình 
ta làm như sau:
Bước 1: Từ một trong hai phương trình, ta biểu diễn x theo y (hoặc y theo x).
Bước 2: Thế biểu thức vừa rút ra được vào phương trình còn lại rồi giải phương trình ta tìm được x (hoặc y).
Bước 3: Từ x (hoặc y) vừa tìm được, thay lại vào biểu thức ở bước 1 ta tìm được y (hoặc x) rồi kết luận nghiệm.
+ Nếu xuất hiện phương trình dạng 0x = a (hoặc 0y = a) thì ta kết luận hệ phương trình vô nghiệm nếu a ≠ 0 hoặc hệ có vô số nghiệm nếu a = 0.
Bài 16 trang 16: Giải các hệ phương trình sau bằng phương pháp thế:
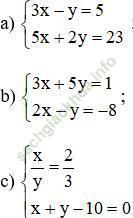
Hướng dẫn giải:
Cách 1:
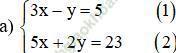
Từ (1) ta rút ra được y = 3x – 5 (*)
Thế (*) vào phương trình (2) ta được:
5x + 2 (3x – 5) = 23 ⇔ 5x + 6x – 10 = 23 ⇔ 11x = 33 ⇔ x = 3.
Thay x = 3 vào (*) ta được y = 3.3 – 5 = 4.
Vậy hệ phương trình có nghiệm duy nhất (3; 4).
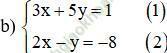
Từ (2) ta rút ra được y = 2x + 8 (*)
Thế (*) vào phương trình (1) ta được:
3x + 5 (2x + 8) = 1 ⇔ 3x + 10x + 40 = 1 ⇔ 13x = -39 ⇔ x = -3.
Thay x = - 3 vào (*) ta được y = 2. (-3) + 8 = 2.
Vậy hệ phương trình có nghiệm duy nhất (-3; 2).
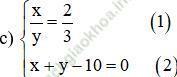
Từ (1) ta rút ra được 
(*)
Thế (*) vào phương trình (2) ta được:
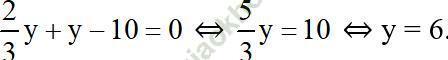
Thay y = 6 vào (*) ta được x = 4.
Vậy hệ phương trình có nghiệm duy nhất (x; y) = (4; 6).
Cách 2:
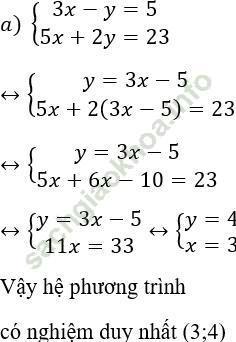
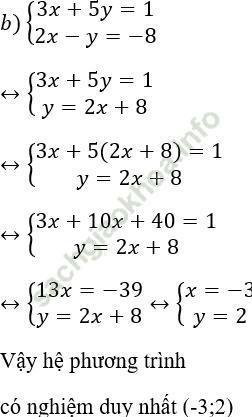
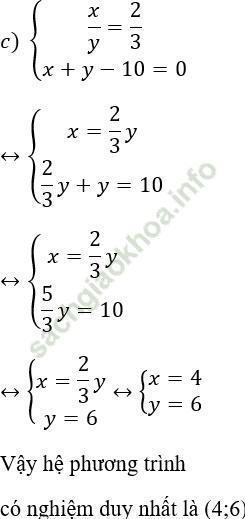
Giải hệ phương trình 
ta làm như sau:
Bước 1: Từ một trong hai phương trình, ta biểu diễn x theo y (hoặc y theo x).
Bước 2: Thế biểu thức vừa rút ra được vào phương trình còn lại rồi giải phương trình ta tìm được x (hoặc y).
Bước 3: Từ x (hoặc y) vừa tìm được, thay lại vào biểu thức ở bước 1 ta tìm được y (hoặc x) rồi kết luận nghiệm.
Bài 17 trang 16: Giải các hệ phương trình sau bằng phương pháp thế:
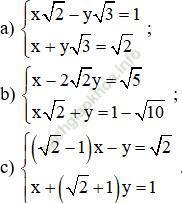
Hướng dẫn giải:
Cách 1:
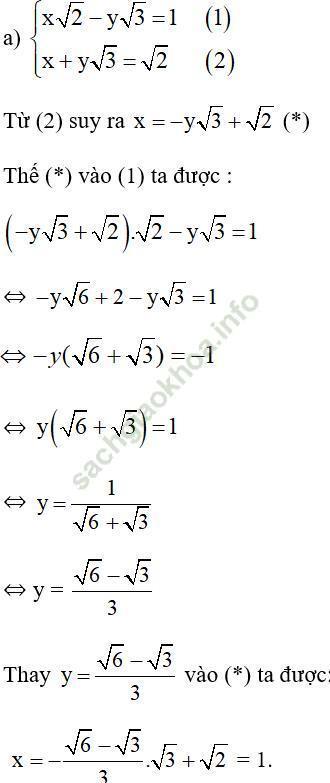
Vậy hệ phương trình có nghiệm duy nhất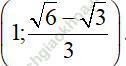 
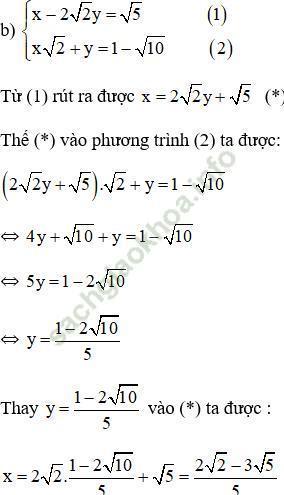
Vậy hệ phương trình có nghiệm duy nhất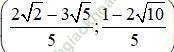 
Vậy hệ phương trình có nghiệm duy nhất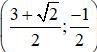 
Cách 2:
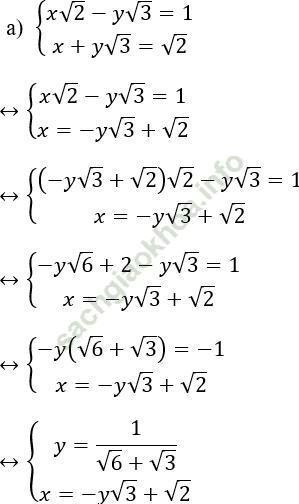
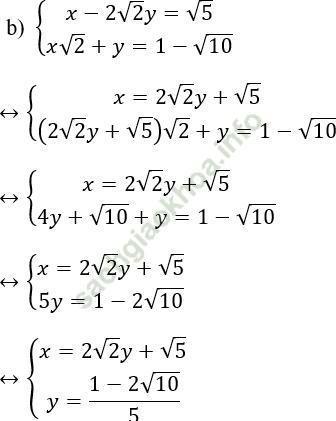
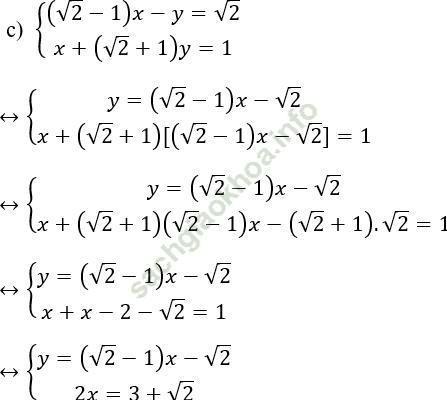
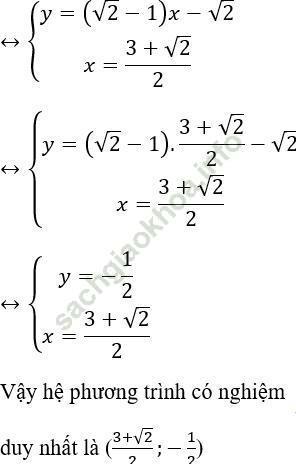
Giải hệ phương trình 
ta làm như sau:
Bước 1: Từ một trong hai phương trình, ta biểu diễn x theo y (hoặc y theo x).
Bước 2: Thế biểu thức vừa rút ra được vào phương trình còn lại rồi giải phương trình ta tìm được x (hoặc y).
Bước 3: Từ x (hoặc y) vừa tìm được, thay lại vào biểu thức ở bước 1 ta tìm được y (hoặc x) rồi kết luận nghiệm.
Bài 18 trang 16:
a) Xác định các hệ số a và b, biết rằng hệ phương trình
có nghiệm (1; -2).Hướng dẫn giải:
a) Hệ phương trình 
có nghiệm (1; -2) khi và chỉ khi (1; -2) thỏa mãn hệ phương trình. Thay x = 1, y = -2 vào hệ phương trình ta được:
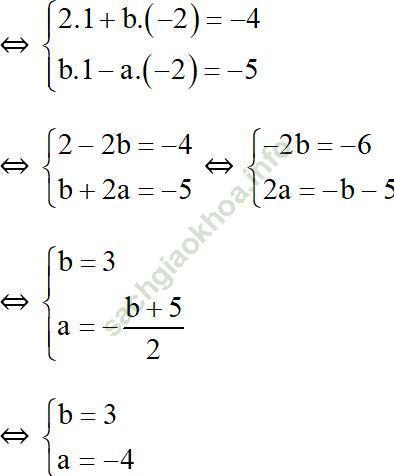
Vậy với a = -4 và b = 3 thì hệ phương trình nhận (1; -2) là nghiệm.
b) Hệ phương trình có nghiệm (√2 - 1; √2)khi và chỉ khi (√2 - 1; √2)thỏa mãn hệ phương trình. Thay (√2 - 1; √2)vào hệ phương trình ta được:
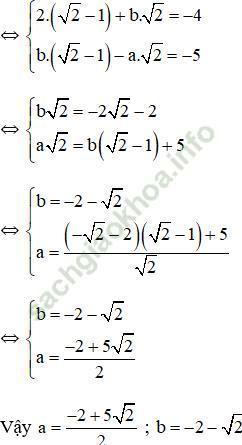
Bài 19 trang 16: Biết rằng: Đa thức P (x) chia hết cho đa thức x – a khi và chỉ khi P (a) = 0. Hãy tìm các giá trị của m và n sao cho đa thức sau đồng thời chia hết cho x + 1 và x – 3:
P (x) = mx3 + (m – 2)x2 – (3n – 5)x – 4n
Hướng dẫn giải:
+) P (x) chia hết cho x + 1
⇔ P (-1) = 0
⇔ m. (-1)3 + (m – 2)(-1)2 – (3n – 5). (-1) – 4n = 0
⇔ -m + m – 2 + 3n – 5 – 4n = 0
⇔ -n – 7 = 0
⇔ n = -7 (1)
+ P (x) chia hết cho x – 3
⇔ P (3) = 0
⇔ m. 33 + (m – 2).32 – (3n – 5).3 – 4n = 0
⇔ 27m + 9m – 18 – 9n + 15 – 4n = 0
⇔ 36m – 13n = 3 (2)
Từ (1) và (2) ta có hệ phương trình:
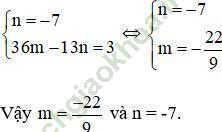
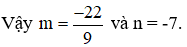thì đa thức P (x) đồng thời chia hết cho x + 1 và x – 3