Bài 7: Phương trình quy về phương trình bậc hai - trang 55 Toán 9 Tập 2

a) x4 – 5x2 + 4 = 0;

b) 2x4 – 3x2 – 2 = 0;

c) 3x4 + 10x2 + 3 = 0

Hướng dẫn giải:

a) x4 – 5x2 + 4 = 0 (1)

Đặt x2 = t, điều kiện t ≥ 0.

Khi đó (1) trở thành: t2 – 5t + 4 = 0 (2)

Giải (2): Có a = 1; b = -5; c = 4 ⇒ a + b + c = 0

⇒ Phương trình có hai nghiệm t1 = 1; t2 = c/a = 4

Cả hai giá trị đều thỏa mãn điều kiện.

+ Với t = 1 ⇒ x2 = 1 ⇒ x = 1 hoặc x = -1;

+ Với t = 4 ⇒ x2 = 4 ⇒ x = 2 hoặc x = -2.

Vậy phương trình (1) có tập nghiệm S = {-2; -1; 1; 2}.

b) 2x4 – 3x2 – 2 = 0; (1)

Đặt x2 = t, điều kiện t ≥ 0.

Khi đó (1) trở thành: 2t2 – 3t – 2 = 0 (2)

Giải (2): Có a = 2; b = -3; c = -2

⇒ Δ = (-3)2 - 4.2. (-2) = 25 > 0

⇒ Phương trình có hai nghiệm

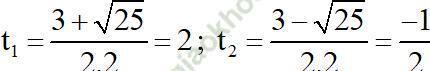
Chỉ có giá trị t1 = 2 thỏa mãn điều kiện.

+ Với t = 2 ⇒ x2 = 2 ⇒ x = √2 hoặc x = -√2;

Vậy phương trình (1) có tập nghiệm S = {-√2; √2}.

c) 3x4 + 10x2 + 3 = 0 (1)

Đặt x2 = t, điều kiện t ≥ 0.

Khi đó (1) trở thành: 3t2 + 10t + 3 = 0 (2)

Giải (2): Có a = 3; b' = 5; c = 3

⇒ Δ’ = 52 – 3.3 = 16 > 0

⇒ Phương trình có hai nghiệm phân biệt

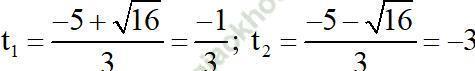
Cả hai giá trị đều không thỏa mãn điều kiện.

Vậy phương trình (1) vô nghiệm.

Phương trình có dạng: ax⁴ + bx² + c = 0 (a ≠ 0) gọi là phương trình trùng phương.

Cách giải phương trình trùng phương:

Bước 1: Đặt x² = t; t ≥ 0. Khi đó ta đưa được phương trình ban đầu về phương trình bậc hai ẩn t.

Bước 2: Giải phương trình bậc hai ẩn t, đối chiếu với điều kiện t ≥ 0.

Bước 3: Từ nghiệm t vừa tìm được, ta thay trở lại x² = t để tìm x và kết luận nghiệm.

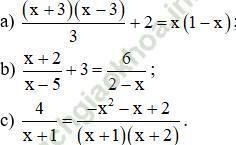
Hướng dẫn giải:

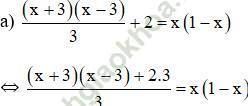
⇔ (x + 3)(x – 3) + 2.3 = 3x (1 – x)

⇔ x2 – 9 + 6 = 3x – 3x2

⇔ x2 – 9 + 6 – 3x + 3x2 = 0

⇔ 4x2 – 3x – 3 = 0

Có a = 4; b = -3; c = -3 ⇒ Δ = (-3)2 – 4.4. (-3) = 57 > 0

Phương trình có hai nghiệm

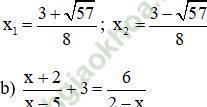
Điều kiện xác định: x ≠ 5; x ≠ 2.

Quy đồng và khử mẫu ta được:

(x + 2)(2 – x) + 3 (2 – x)(x – 5) = 6 (x – 5)

⇔ 4 – x2 + 6x – 3x2 – 30 + 15x = 6x – 30

⇔ 4 – x2 + 6x – 3x2 – 30 + 15x – 6x + 30 = 0

⇔ -4x2 + 15x + 4 = 0

Có a = -4; b = 15; c = 4 ⇒ Δ = 152 – 4. (-4).4 = 289 > 0

Phương trình có hai nghiệm phân biệt:

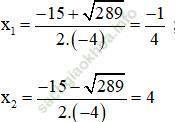
Cả hai giá trị đều thỏa mãn điều kiện.

Vậy phương trình có tập nghiệm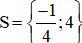

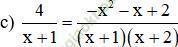
Điều kiện xác định: x ≠ -1; x ≠ -2.

Quy đồng và khử mẫu ta được:

4. (x + 2) = -x2 – x + 2

⇔ 4x + 8 = -x2 – x + 2

⇔ 4x + 8 + x2 + x – 2 = 0

⇔ x2 + 5x + 6 = 0.

Có a = 1; b = 5; c = 6 ⇒ Δ = 52 – 4.1.6 = 1 > 0

⇒ Phương trình có hai nghiệm phân biệt:

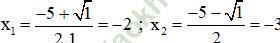
Chỉ có nghiệm x2 = -3 thỏa mãn điều kiện xác định.

Vậy phương trình có nghiệm x = -3.

Cách giải phương trình chứa ẩn ở mẫu thức:

Bước 1: Tìm điều kiện xác định của phương trình.

Bước 2: Quy đồng, khử mẫu

Bước 3: Giải phương trình nhận được

Bước 4: Đối chiếu nghiệm thu được với điều kiện xác định và kết luận nghiệm.

a) (3x2 – 5x + 1)(x2 – 4) = 0;

b) (2x2 + x – 4)2 – (2x – 1)2 = 0.

Hướng dẫn giải:

a) (3x2 – 5x + 1)(x2 – 4) = 0

⇔ 3x2 – 5x + 1 = 0 (1)

hoặc x2 – 4 = 0 (2)

+ Giải (1): 3x2 – 5x + 1 = 0

Có a = 3; b = -5; c = 1 ⇒ Δ = (-5)2 – 4.3 = 13 > 0

Phương trình có hai nghiệm: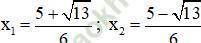

+ Giải (2): x2 – 4 = 0 ⇔ x2 = 4 ⇔ x = 2 hoặc x = -2.

Vậy phương trình có tập nghiệm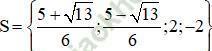

b) (2x2 + x – 4)2 – (2x – 1)2 = 0

⇔ (2x2 + x – 4 – 2x + 1)(2x2 + x – 4 + 2x – 1) = 0

⇔ (2x2 – x – 3)(2x2 + 3x – 5) = 0

⇔ 2x2 – x – 3 = 0 (1)

hoặc 2x2 + 3x – 5 = 0 (2)

+ Giải (1): 2x2 – x – 3 = 0

Có a = 2; b = -1; c = -3 ⇒ a – b + c = 0

⇒ Phương trình có hai nghiệm x = -1 và x = -c/a = 3/2.

+ Giải (2): 2x2 + 3x – 5 = 0

Có a = 2; b = 3; c = -5 ⇒ a + b + c = 0

⇒ Phương trình có hai nghiệm x = 1 và x = c/a = -5/2.

Vậy phương trình có tập nghiệm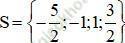

+ Phương trình tích: A (x).B (x).C (x)…. = 0 ⇔

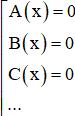
+ Nếu phương trình ax² + bx + c = 0 (a ≠ 0) có a + b + c = 0 thì phương trình có một nghiệm x₁ = 1; nghiệm còn lại x₂ = c/a.

+ Nếu phương trình ax² + bx + c = 0 (a ≠ 0) có a – b + c = 0 thì phương trình có một nghiệm x₁ = -1; nghiệm còn lại x₂ = -c/a.