Luyện tập trang 45-46 - SGK Toán 9 Tập 1

Bài 1: Nhắc lại và bổ sung các khái niệm về hàm số Luyện tập (trang 45-46 sgk Toán 9 Tập 1)

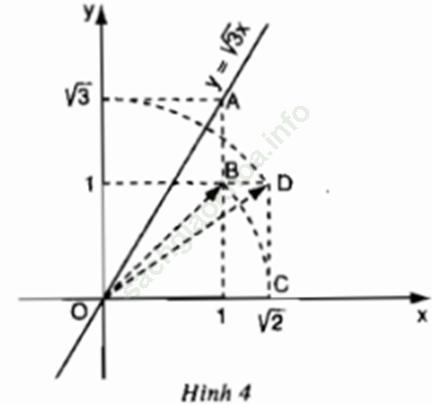
Bài 4 (trang 45 SGK Toán 9 Tập 1): Đồ thị hàm số y = √ 3 x được vẽ bằng compa và thước thẳng ở hình 4. Hãy tìm hiểu và trình bày lại các bước thực hiện vẽ đồ thị đó.

Hướng dẫn giải:

- Cách vẽ:

+ Cho x = 1 ta được y = √ 3.1 = √ 3

+ Dựng điểm A (1; √ 3). Vẽ đường thẳng qua O, A được đồ thị hàm số y = √ 3 x.

- Các bước vẽ đồ thị hàm số y = √ 3 x.

+ Dựng điểm B (1; 1). Vẽ OB ta được

+ Dựng điểm √ 2 trên trục hoành Ox: vẽ cung tròn bán kính OC = √ 2, cắt Ox tạ điểm có hoành độ là √ 2.

+ Dựng điểm D (√ 2; 1). Vẽ OD ta được

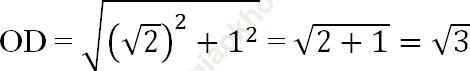
+ Dựng điểm √ 3 trên trục tung Ox: Vẽ cung tròn bán kính OD = √ 3 cắt Oy tại điểm có tung độ là √ 3.

+ Dựng điểm A (1; √ 3)

+ Vẽ đường thẳng O, A ta được đồ thị hàm số y = √ 3 x.

Bài 5 (trang 45):

a) Vẽ đồ thị của các hàm số y = x và y = 2x trên cùng một mặt phẳng tọa độ Oxy (hình 5).

b) Đường thẳng song song với trục Ox và cắt trục Oy tại các điểm có tung độ y = 4 lần lượt cắt các đường thẳng y = 2x, y = x tại hai điểm A và B.

Tìm tọa độ các điểm A, B, tính chu vi, diện tích của tam giác OAB theo đơn vị đo trên các trục tọa độ là xentimet

Hình 5

Hướng dẫn giải:

a) Vẽ đồ thị:

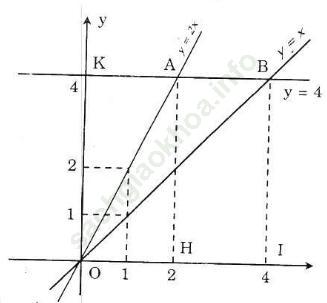
b) - Từ hình vẽ ta có: y_A = y_B = 4 suy ra:.

+ Hoành độ của A: 4 = 2. x_A => x_A = 2 (*)

+ Hoành độ của B: 4 = x_B => x_B = 4

=> Tọa độ 2 điểm là: A (2,4); B (4,4)

- Tìm độ dài các cạnh của Δ OAB

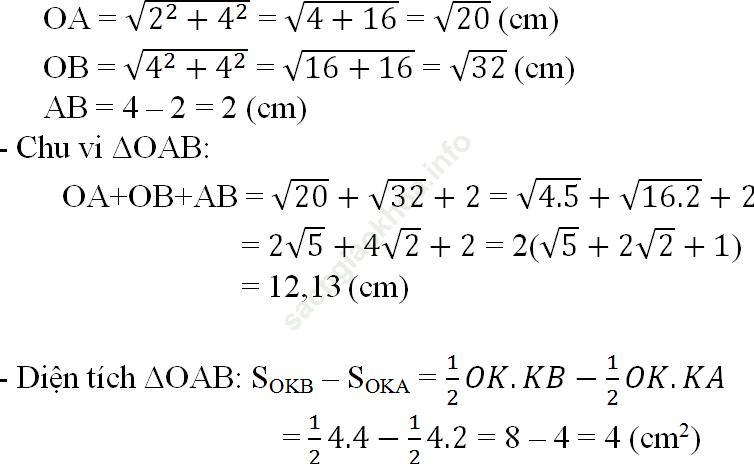
( (*): muốn tìm tung độ hay hoành độ của một điểm khi đã biết trước hoành độ hay tung độ, ta thay chúng vào phương trình đồ thị hàm số để tìm đơn vị còn lại. )

Bài 6 (trang 45): Cho các hàm số y = 0,5x và y = 0,5x + 2.

a) Tính giá trị y tương ứng của mỗi hàm số theo giá trị đã cho của biến x rồi điền vào bảng sau:

x	-2,5	-2,25	-1,5	-1	0	1	1,5	2,25	2,5
y = 0,5x
y = 0,5x + 2

b) Có nhận xét gì về các giá trị tương ứng của hai hàm số đó khi biến x lấy cùng một giá trị?

Hướng dẫn giải:

a) Sau khi tính giá trị của mỗi giá trị theo các giá trị của x đã cho ta được bảng sau:

x	-2,5	-2,25	-1,5	-1	0	1	1,5	2,25	2,5
y = 0,5x	-1,25	-1,125	-0,75	-0,5	0	0,5	0,75	1,125	1,25
y = 0,5x + 2	0,75	0,875	1,25	1,5	2	2,5	2,75	3,125	3,25

b) Nhận xét: Cùng một giá trị của biến x, giá trị của hàm số y = 0,5x + 2 luôn luôn lớn hơn giá trị tương ứng của hàm số y = 0,5x là 2 đơn vị.

Bài 7 (trang 46): Cho hàm số y = f (x) = 3x.

Cho x hai giá trị bất kì x₁, x₂ sao cho x₁ < x₂.

Hãy chứng minh f (x₁) < f (x₂) rồi rút ra kết luận hàm số đã cho đồng biến trên R.

Hướng dẫn giải:

Cho x các giá trị bất kì x₁, x₂ sao cho x₁ < x₂

=> x₁ - x₂ < 0

Ta có: f (x₁) = 3x₁; f (x₂) = 3x₂

=> f (x₁) - f (x₂) = 3x₁ - 3x₂ = 3 (x₁ - x₂) < 0

=> f (x₁) < f (x₂)

Vậy với x₁ < x₂ ta được f (x₁) < f (x₂) nên hàm số y = 3x đồng biến trên tập hợp số thực R.

Bài trước: Bài 1: Nhắc lại và bổ sung các khái niệm về hàm số - trang 43 Toán 9 Tập 1 Bài tiếp: Bài 2: Hàm số bậc nhất - trang 46 Toán 9 Tập 1